Содержание
- 2. Уравнения эллиптического типа Закон сохранения массы жидкости в выделенном объеме V С силу произвольного выбора объема
- 3. Уравнения эллиптического типа Рассмотрим установившееся течение жидкости, для которого ее скорость не зависит от времени:
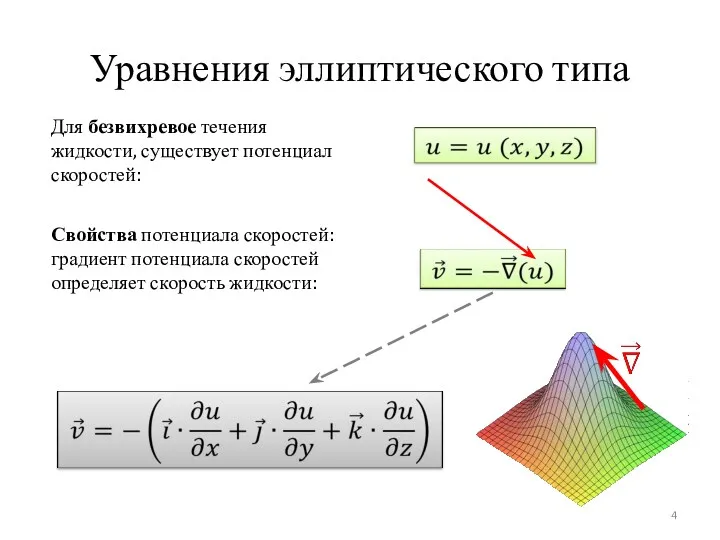
- 4. Уравнения эллиптического типа Для безвихревое течения жидкости, существует потенциал скоростей: Свойства потенциала скоростей: градиент потенциала скоростей
- 5. Уравнения эллиптического типа Для потенциала скоростей, справедливо уравнение Лапласа: здесь оператор Лапласа Laplace, Pierre-Simon (1749–1827), французский
- 6. Уравнения эллиптического типа Johann Carl Friedrich Gauß; 1777-1855, Гёттинген): немецкий математик, механик, физик, астроном и геодезист.
- 7. Уравнения эллиптического типа С помощью теоремы Остроградского-Гаусса преобразуем последнее выражение к дифференциальной форме: или
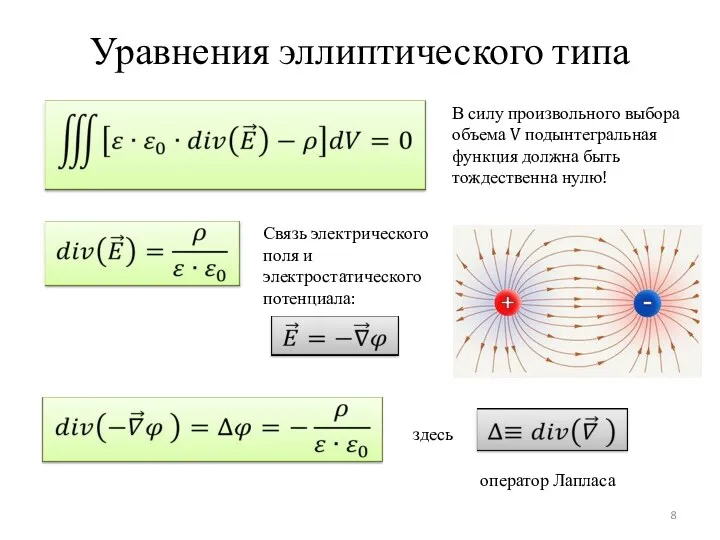
- 8. Уравнения эллиптического типа В силу произвольного выбора объема V подынтегральная функция должна быть тождественна нулю! Связь
- 9. Уравнения эллиптического типа Для электростатического потенциала справедливо уравнение Пуассона: Siméon Denis Poisson (1781-1840, Франция), французский математик,
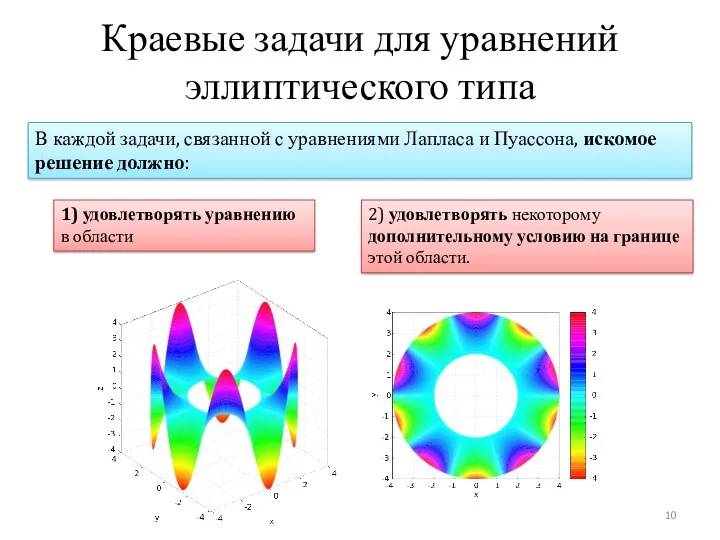
- 10. Краевые задачи для уравнений эллиптического типа В каждой задачи, связанной с уравнениями Лапласа и Пуассона, искомое
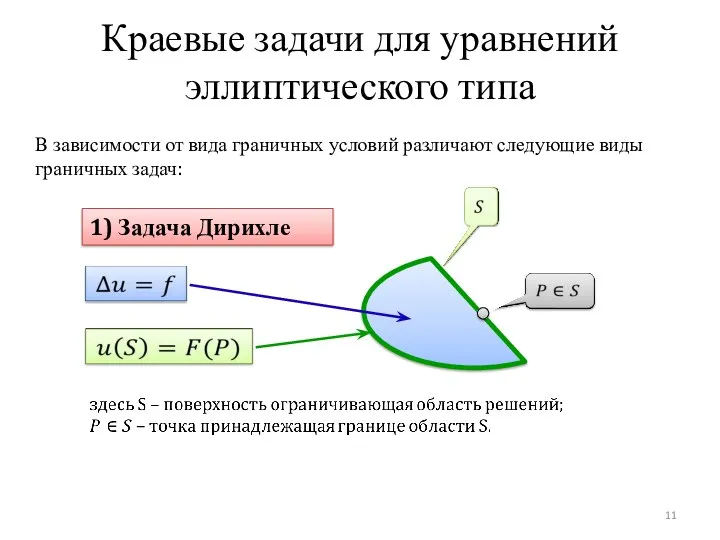
- 11. Краевые задачи для уравнений эллиптического типа 1) Задача Дирихле В зависимости от вида граничных условий различают
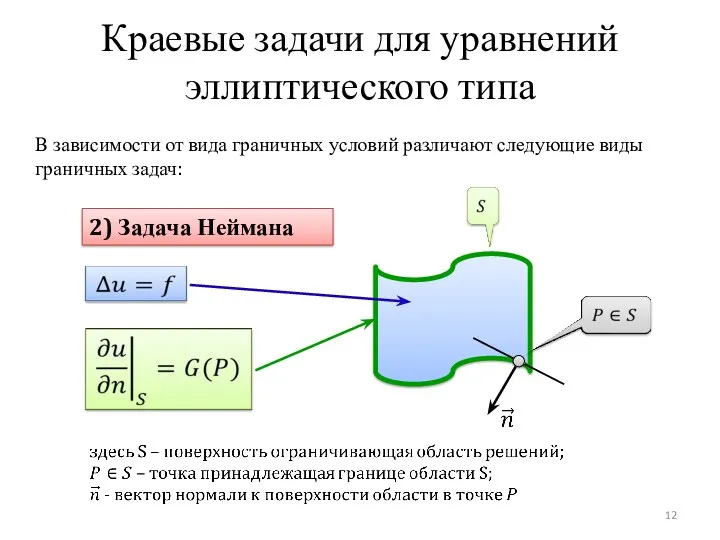
- 12. Краевые задачи для уравнений эллиптического типа 2) Задача Неймана В зависимости от вида граничных условий различают
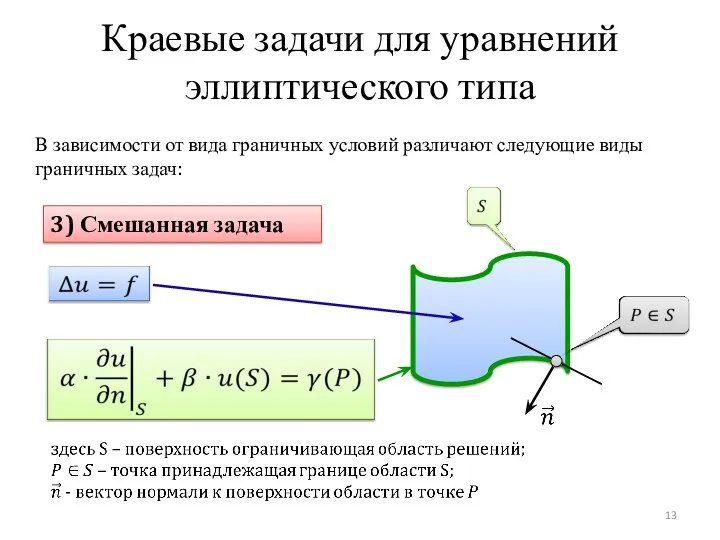
- 13. Краевые задачи для уравнений эллиптического типа 3) Смешанная задача В зависимости от вида граничных условий различают
- 14. Уравнения параболического типа Процесс передачи теплоты от более нагретых частей тела к менее нагретым связан с
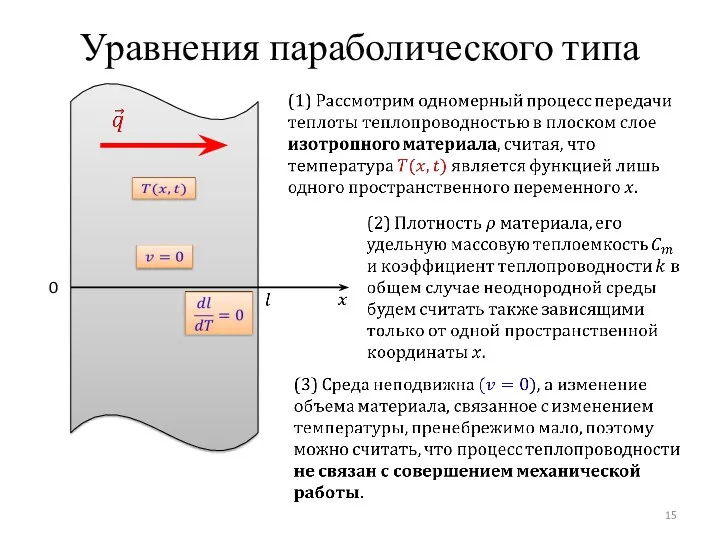
- 15. Уравнения параболического типа 0
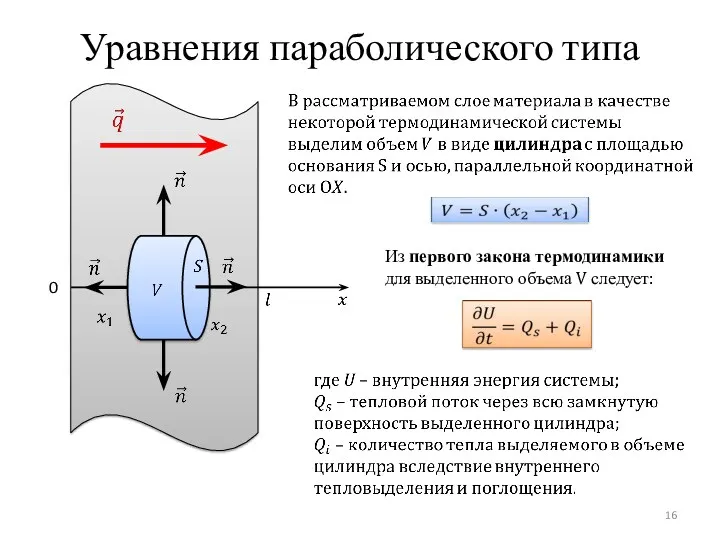
- 16. Уравнения параболического типа 0 Из первого закона термодинамики для выделенного объема V следует:
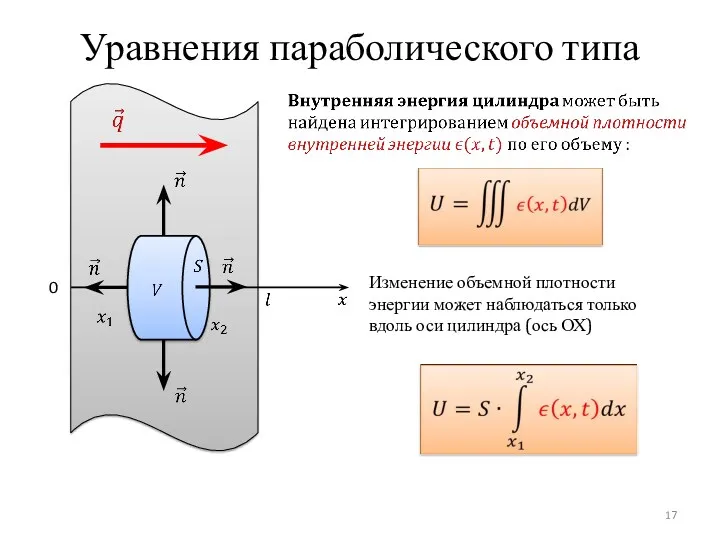
- 17. Уравнения параболического типа 0 Изменение объемной плотности энергии может наблюдаться только вдоль оси цилиндра (ось ОХ)
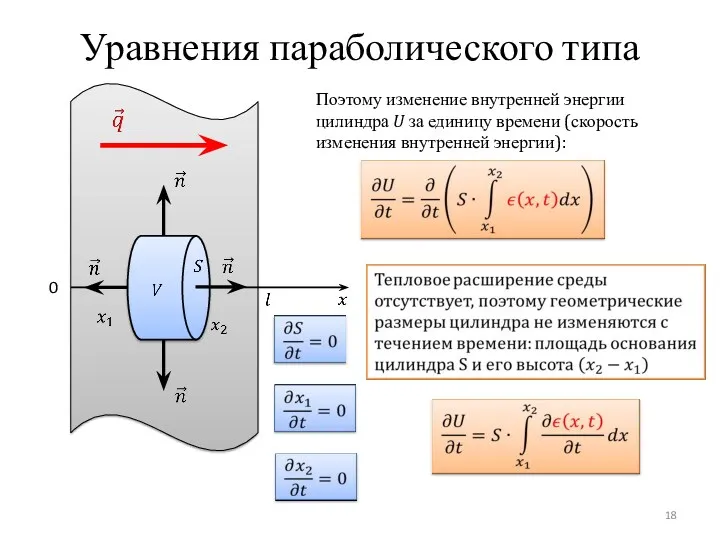
- 18. Уравнения параболического типа 0 Поэтому изменение внутренней энергии цилиндра U за единицу времени (скорость изменения внутренней
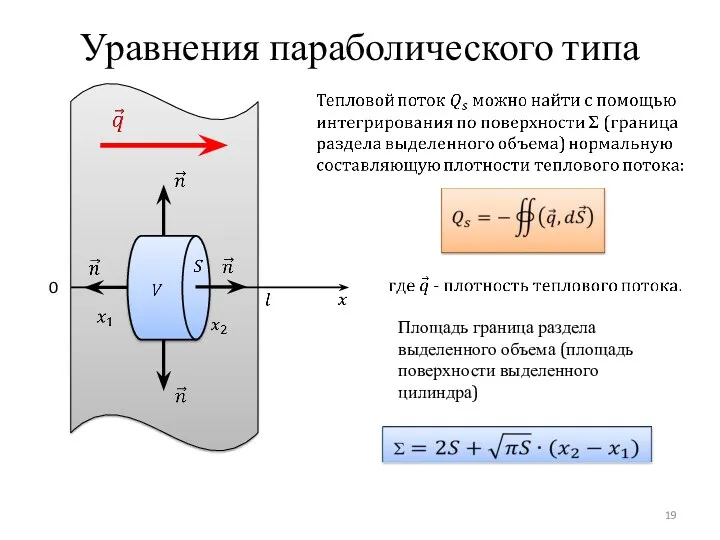
- 19. Уравнения параболического типа 0 Площадь граница раздела выделенного объема (площадь поверхности выделенного цилиндра)
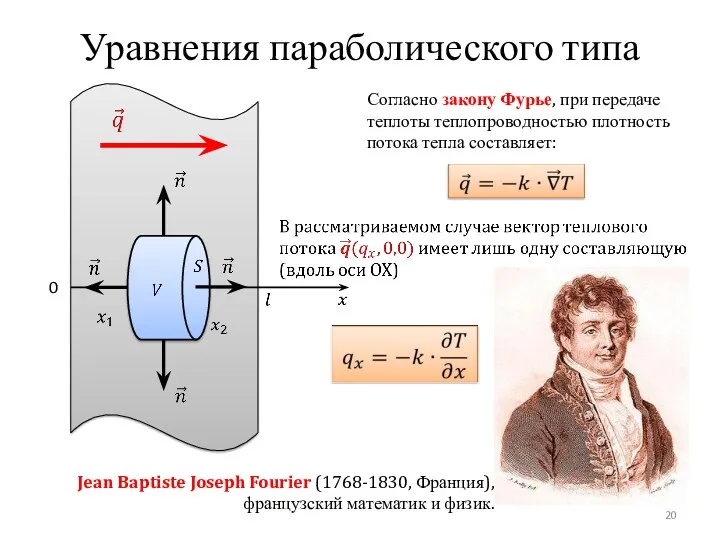
- 20. Уравнения параболического типа 0 Согласно закону Фурье, при передаче теплоты теплопроводностью плотность потока тепла составляет: Jean
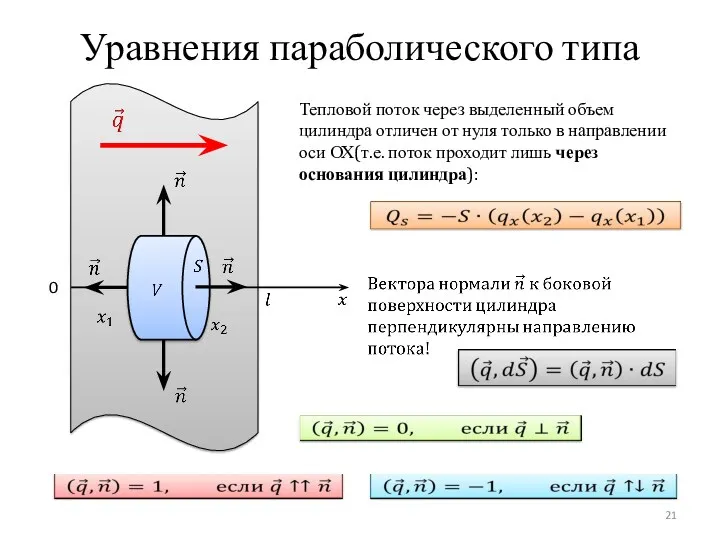
- 21. Уравнения параболического типа 0 Тепловой поток через выделенный объем цилиндра отличен от нуля только в направлении
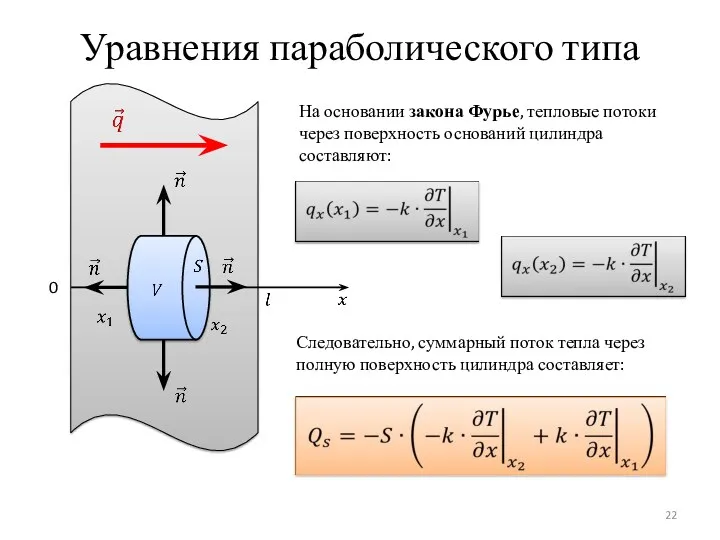
- 22. Уравнения параболического типа 0 На основании закона Фурье, тепловые потоки через поверхность оснований цилиндра составляют: Следовательно,
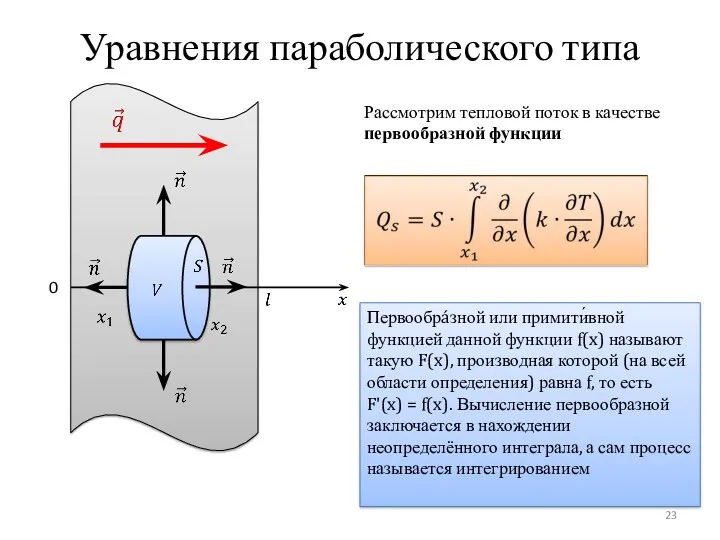
- 23. Уравнения параболического типа 0 Рассмотрим тепловой поток в качестве первообразной функции Первообрáзной или примити́вной функцией данной
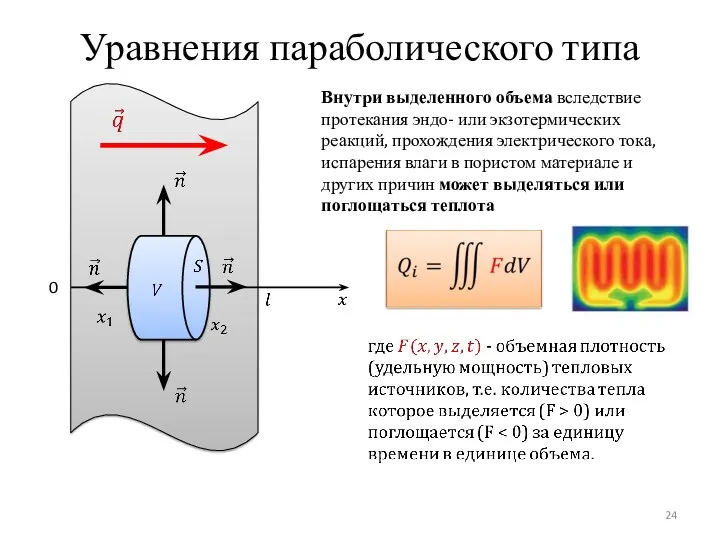
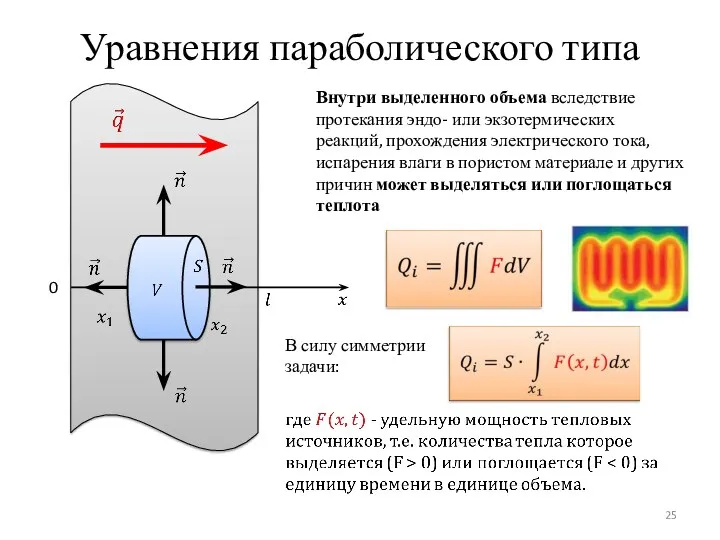
- 24. Уравнения параболического типа 0 Внутри выделенного объема вследствие протекания эндо- или экзотермических реакций, прохождения электрического тока,
- 25. Уравнения параболического типа 0 Внутри выделенного объема вследствие протекания эндо- или экзотермических реакций, прохождения электрического тока,
- 26. Уравнения параболического типа Таким образом, из первого закона термодинамики (закон сохранения и превращения энергии) следует: Подстановка
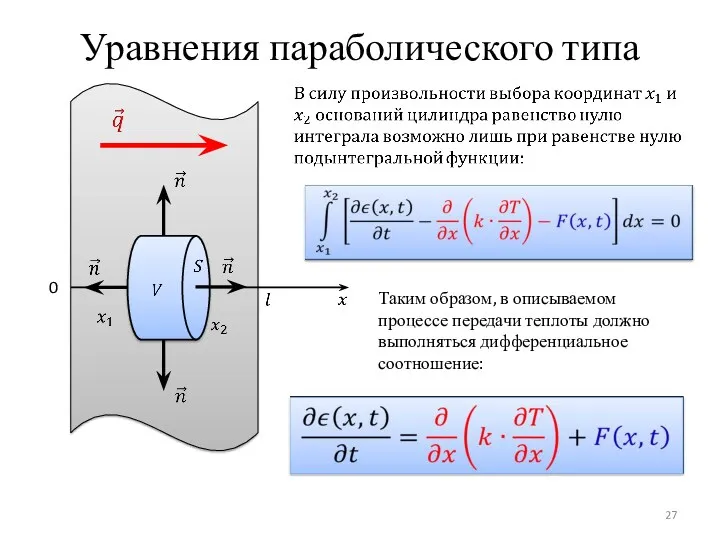
- 27. Уравнения параболического типа 0 Таким образом, в описываемом процессе передачи теплоты должно выполняться дифференциальное соотношение:
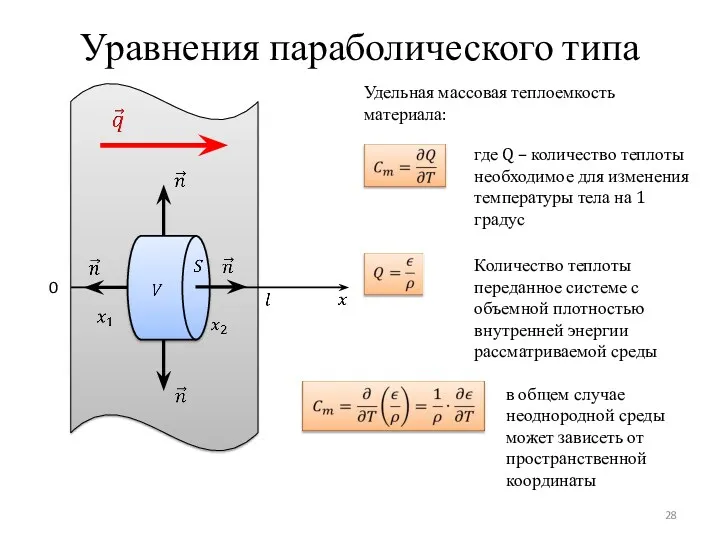
- 28. Уравнения параболического типа 0 Удельная массовая теплоемкость материала: где Q – количество теплоты необходимое для изменения
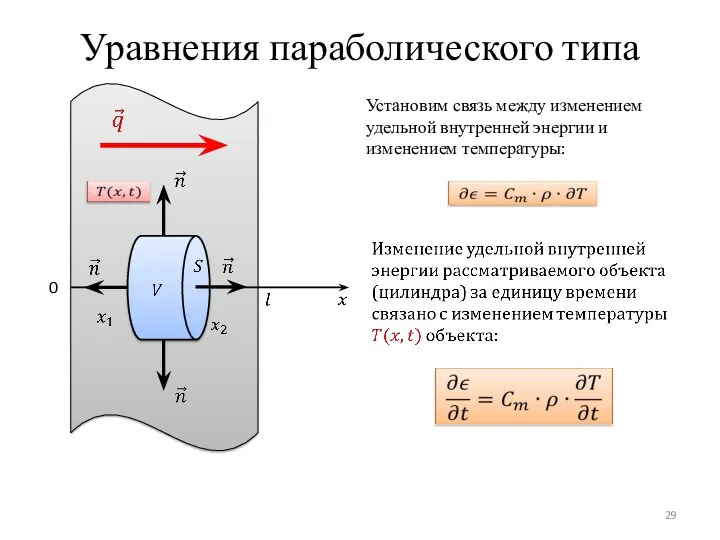
- 29. Уравнения параболического типа 0 Установим связь между изменением удельной внутренней энергии и изменением температуры:
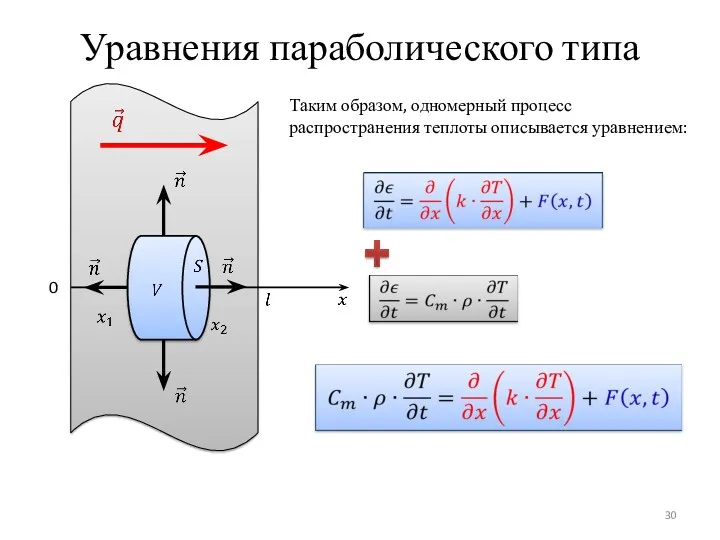
- 30. Уравнения параболического типа 0 Таким образом, одномерный процесс распространения теплоты описывается уравнением:
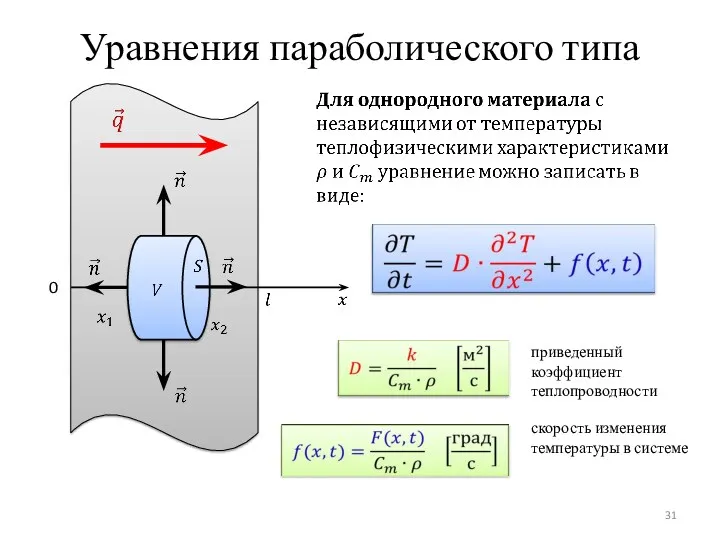
- 31. Уравнения параболического типа 0 приведенный коэффициент теплопроводности скорость изменения температуры в системе
- 32. Уравнения параболического типа Полученное уравнение является дифференциальными уравнением в частных производных параболического типа Эти уравнения лежат
- 33. Уравнения параболического типа. Начальные и граничные условия Чтобы с помощью уравнения параболического типа можно было описать
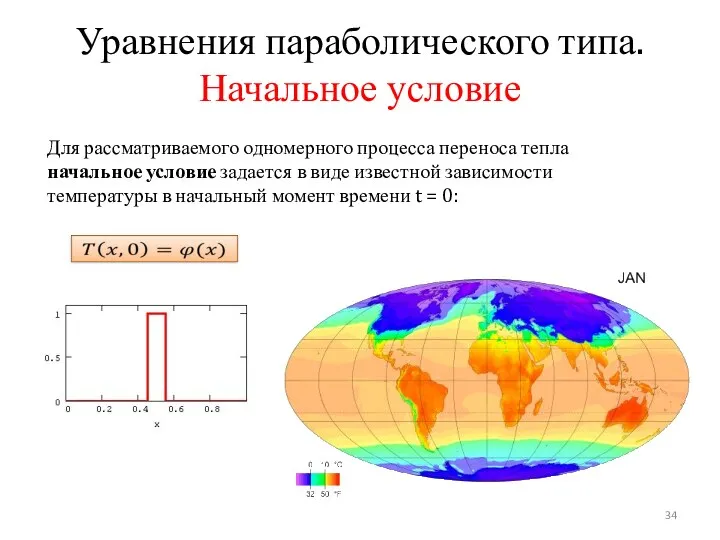
- 34. Уравнения параболического типа. Начальное условие Для рассматриваемого одномерного процесса переноса тепла начальное условие задается в виде
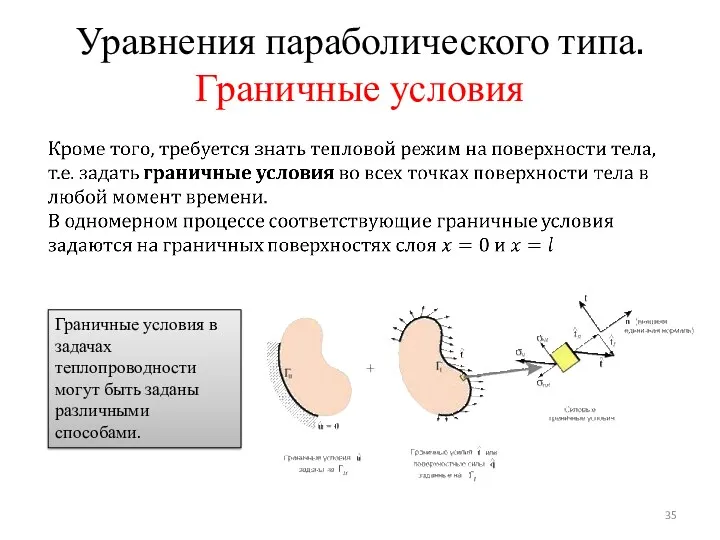
- 35. Уравнения параболического типа. Граничные условия Граничные условия в задачах теплопроводности могут быть заданы различными способами.
- 36. Уравнения параболического типа. Граничные условия 1) Граничное условие первого рода, когда в каждой точке поверхности тела
- 37. Уравнения параболического типа. Граничные условия 2) Граничное условие второго рода, когда на поверхности тела задается тепловой
- 38. Уравнения параболического типа. Граничные условия
- 39. Уравнения параболического типа. Граничные условия 4) При описании температурных полей в многослойных структурах и оболочках на
- 40. Уравнения параболического типа. Граничные условия 5) Граничные условия для неидеального теплового контакта, т.е. когда теплообмен между
- 41. Уравнения параболического типа. Граничные условия 6) Нелинейное граничное условие формулируется в случае если основным механизмом теплообмена
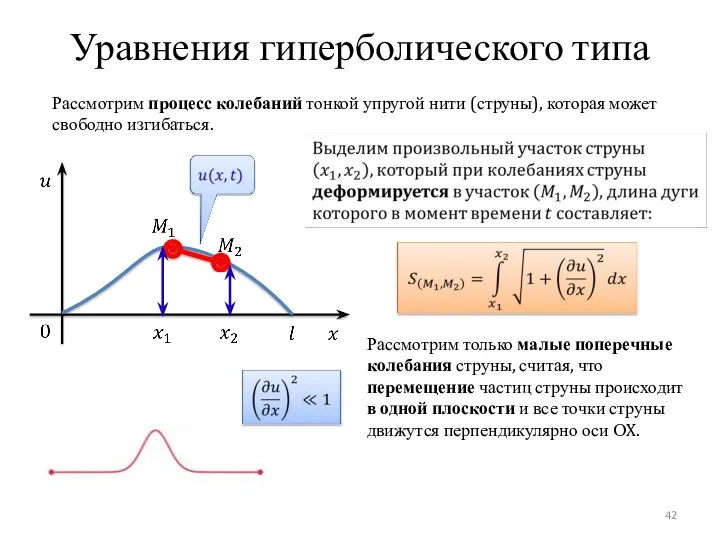
- 42. Уравнения гиперболического типа Рассмотрим процесс колебаний тонкой упругой нити (струны), которая может свободно изгибаться. Рассмотрим только
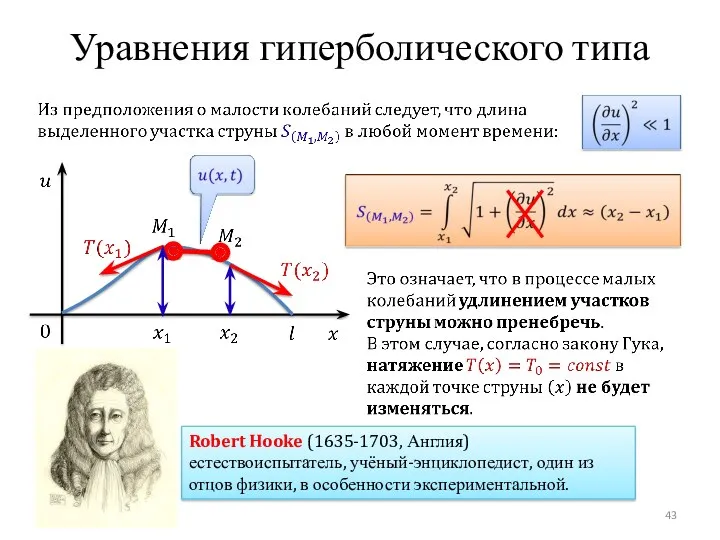
- 43. Уравнения гиперболического типа Robert Hooke (1635-1703, Англия) естествоиспытатель, учёный-энциклопедист, один из отцов физики, в особенности экспериментальной.
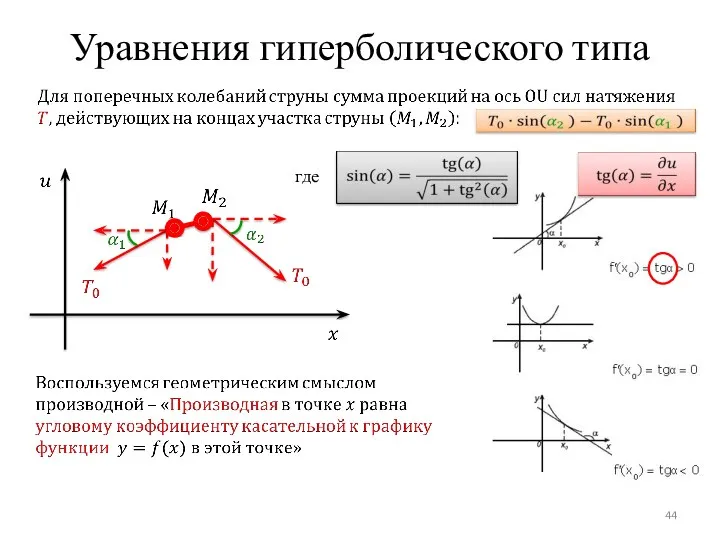
- 44. Уравнения гиперболического типа где
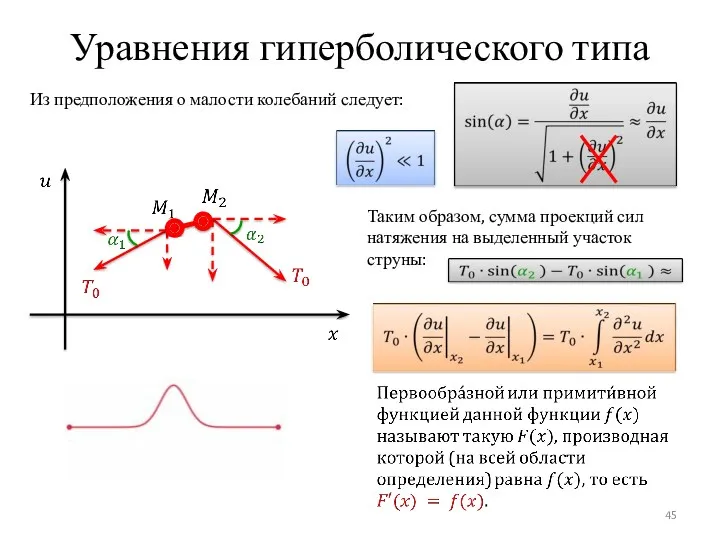
- 45. Уравнения гиперболического типа Из предположения о малости колебаний следует: Таким образом, сумма проекций сил натяжения на
- 46. Уравнения гиперболического типа Закон динамики поступательного движения (закон Ньютона), который для механической системы: Sir Isaac Newton
- 47. Уравнения гиперболического типа Sir Isaac Newton (1643-1727, Англия). Физик, математик, механик и астроном, один из создателей
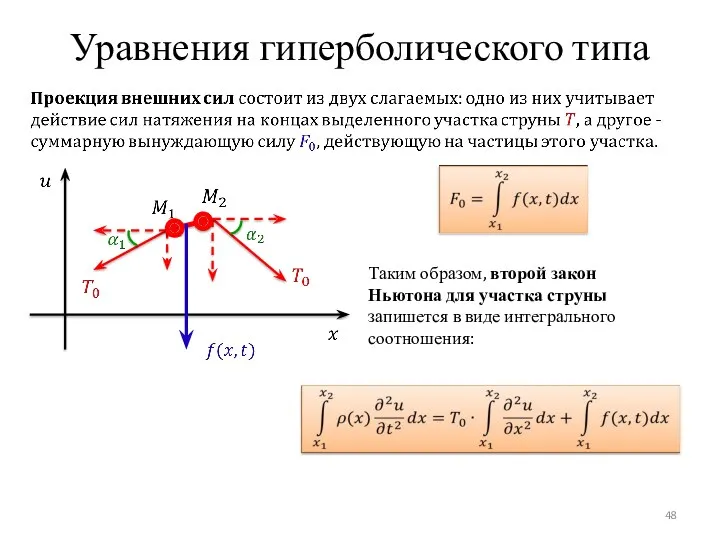
- 48. Уравнения гиперболического типа Таким образом, второй закон Ньютона для участка струны запишется в виде интегрального соотношения:
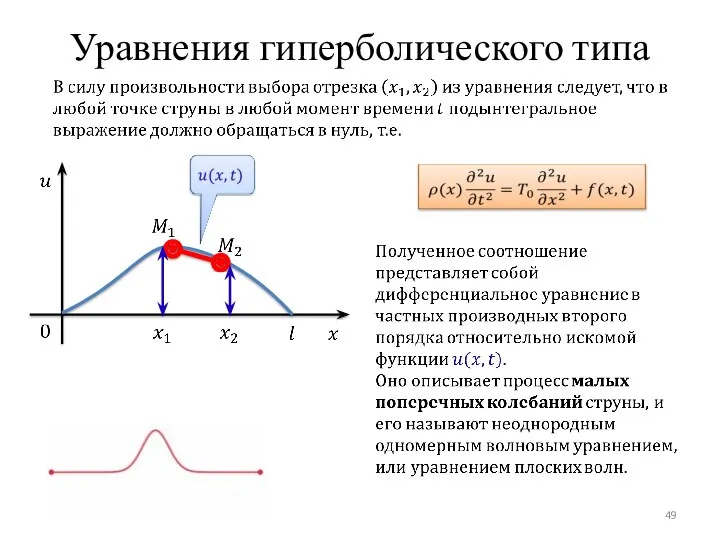
- 49. Уравнения гиперболического типа
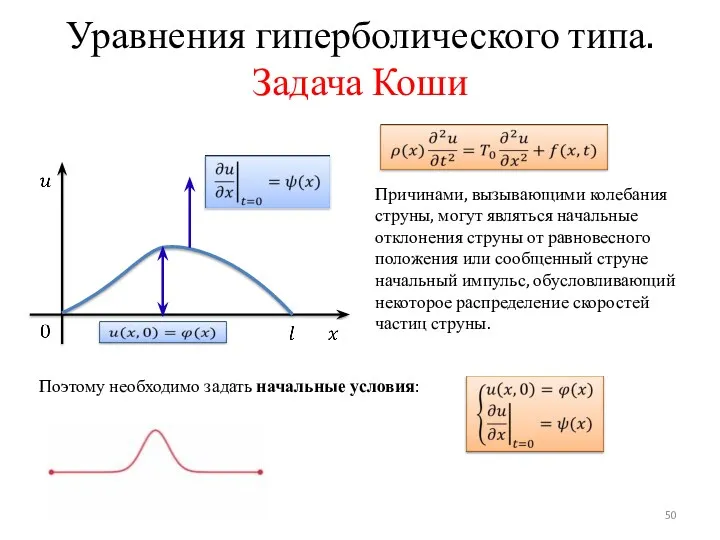
- 50. Уравнения гиперболического типа. Задача Коши Причинами, вызывающими колебания струны, могут являться начальные отклонения струны от равновесного
- 51. Методы решения уравнений в частных производных. Метод Фурье Метод разделения переменных, или метод Фурье, является одним
- 53. Скачать презентацию



















 Обратные задачи
Обратные задачи Классическое определение вероятности
Классическое определение вероятности Экстремум функции двух переменных
Экстремум функции двух переменных Методическая разработка урока математики во 2 классе на тему: Периметр. Программа Школа 2100.
Методическая разработка урока математики во 2 классе на тему: Периметр. Программа Школа 2100. Презентация к уроку математики по теме: Состав числа 5.1 класс. УМК Школа России.
Презентация к уроку математики по теме: Состав числа 5.1 класс. УМК Школа России. Электронное пособие для подготовки к ЕГЭ 2012 год. Подготовка к ЕГЭ
Электронное пособие для подготовки к ЕГЭ 2012 год. Подготовка к ЕГЭ Неделя математики, физики, информатики
Неделя математики, физики, информатики 20231103_kvadratnye_uravneniya._prezentatsiya
20231103_kvadratnye_uravneniya._prezentatsiya Деление трехзначного числа на однозначное
Деление трехзначного числа на однозначное Предел последовательности
Предел последовательности Свойства функции 11 класс
Свойства функции 11 класс Рівняння дотичної до графіка функції
Рівняння дотичної до графіка функції Обобщение темы Четырёхугольники
Обобщение темы Четырёхугольники Уравнение касательной к графику функции
Уравнение касательной к графику функции Табличное сложение. Закрепление знаний
Табличное сложение. Закрепление знаний Памятка по оформлению краткой записи к задачам 1-2 класс
Памятка по оформлению краткой записи к задачам 1-2 класс 20191128_prezentatsiya_ugly
20191128_prezentatsiya_ugly Прицентация дидактической игры Закончи ряд
Прицентация дидактической игры Закончи ряд Теория графов. Определения и примеры. Пути и циклы
Теория графов. Определения и примеры. Пути и циклы Подобные треугольники
Подобные треугольники Решение нелинейных уравнений
Решение нелинейных уравнений Урок математики во 2 классе по теме Трёхзначные числа (Гармония)
Урок математики во 2 классе по теме Трёхзначные числа (Гармония) Устный счёт по математике 2 класс
Устный счёт по математике 2 класс Тренажёр Дартс. Умножение
Тренажёр Дартс. Умножение Тема Окружность
Тема Окружность Цилиндр
Цилиндр Картотека игр по математике
Картотека игр по математике