Mongeova projekcia презентация

Metóda: Sklápanie roviny kolmej na priemetňu
Dané: A[A1, A2], B[B1, B2]. Určte graficky |AB|.
π
x12
x12
ν
zB
a 1
●
a 1
●
A 1
B 1
A
B
λ
≡ p λ1
●
●
●
(A)
(B)
zB
zA
zA
Problém: Určiť graficky dĺžku úsečky danú pôdorysom a nárysom.
|AB|
A 1
B 1
A 2
B 2
●
zA
zB
zA
zB
|AB|
(A)
(B)
≡ p λ 1
a 2
Pa
Pa2
Pa1
l: A1 ∈ l, l ⊥ a1,
Riešenie: Priamkou a = AB preložíme rovinu λ kolmú na priemetňu π. Rovinu λ sklopíme (otočíme o 90º) do priemetne π.
Osou otáčania je priamka a1, kružnica otáčania bodu A leží v rovine kolmej na os otáčania a1 ≡ pλ1, stredom otáčania je A1, polomer otáčania je zA.
Bod A v sklopení – (A) leží na kolmici na a1 v bode A1 a je od neho vzdialený o zA.
Podobne sklopíme bod B, potom |(A)(B)|= |AB|.
k =[A1, r = zA],
4. |(A)(B)|= |AB|.
k ∩ l = (A).
k
l
Vajsáblová, M.: Deskriptívna geometria pre GaK 55

Metóda: Sklápanie roviny kolmej na priemetňu
Definícia: Uhol priamky s priemetňou sa rovná uhlu priamky s jej kolmým priemetom do tejto priemetne: ∠(a, π) = ∠(a1, a)
∠(a, ν) = ∠(a2, a)
x
x12
ν
zB
a 1
●
a 1
●
A 1
B 1
A
B
λ
≡ p λ 1
●
●
●
(A)
(B)
zB
zA
zA
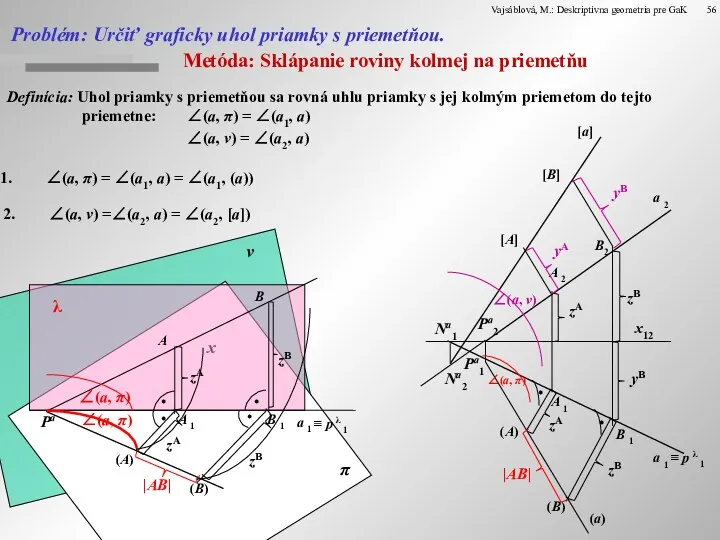
Problém: Určiť graficky uhol priamky s priemetňou.
|AB|
A 1
B 1
A 2
B2
●
zA
zB
zA
zB
|AB|
(A)
(B)
≡ p λ 1
a 2
Pa
Pa2
Pa1
∠(a, π) = ∠(a1, a) = ∠(a1, (a))
∠(a, ν) =∠(a2, a) = ∠(a2, [a])
∠(a, π)
∠(a, π)
[A]
[B]
[a]
(a)
∠(a, ν)
yB
yB
Na2
Na1
∠(a, π)
yA
π
Vajsáblová, M.: Deskriptívna geometria pre GaK 56

π
ν
x12
α
pα1
nα2
pα1
nα2
Isα
●
●
Isα1
Ps1
Ps2
Isα2
Ns1
Ns2
Metóda: Sklápanie roviny kolmej na priemetňu
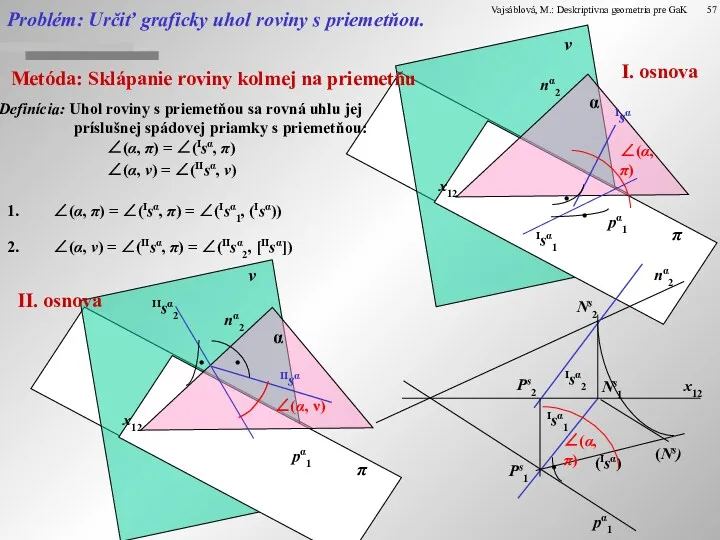
Problém: Určiť graficky uhol roviny s priemetňou.
Definícia: Uhol roviny s priemetňou sa rovná uhlu jej príslušnej spádovej priamky s priemetňou: ∠(α, π) = ∠(Isα, π)
∠(α, ν) = ∠(IIsα, ν)
Isα1
●
(Ns)
∠(α, π)
(Isα)
∠(α, π)
π
ν
α
pα1
nα2
IIsα
●
IIsα2
●
∠(α, ν)
II. osnova
I. osnova
∠(α, π) = ∠(Isα, π) = ∠(Isα1, (Isα))
∠(α, ν) = ∠(IIsα, π) = ∠(IIsα2, [IIsα])
x12
x12
Vajsáblová, M.: Deskriptívna geometria pre GaK 57

x12
π
ν
x12
α
pα1
nα2
pα1
nα2
Ihα
●
●
Ps1
A1
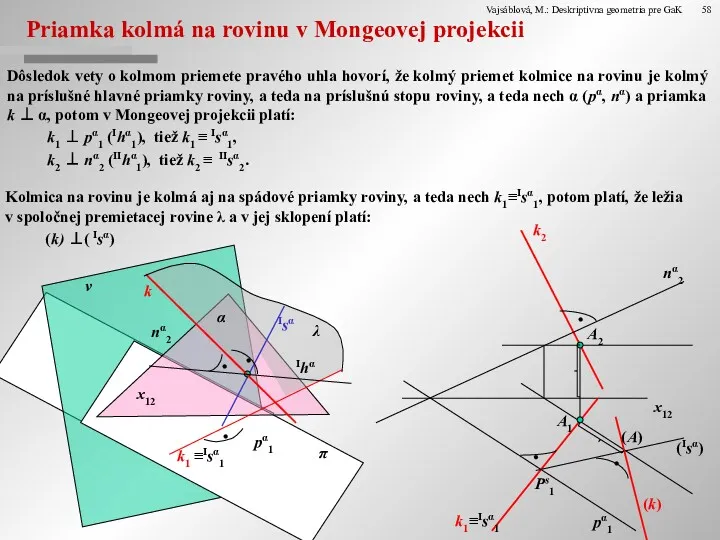
Priamka kolmá na rovinu v Mongeovej projekcii
Dôsledok vety o kolmom priemete pravého uhla hovorí, že kolmý priemet kolmice na rovinu je kolmý na príslušné hlavné priamky roviny, a teda na príslušnú stopu roviny, a teda nech α (pα, nα) a priamka k ⊥ α, potom v Mongeovej projekcii platí:
k1 ⊥ pα1 (Ihα1), tiež k1 ≡ Isα1,
k2 ⊥ nα2 (IIhα1), tiež k2 ≡ IIsα2.
●
(Isα)
A2
k2
(k)
(A)
Isα
k1
●
k
λ
Kolmica na rovinu je kolmá aj na spádové priamky roviny, a teda nech k1≡Isα1, potom platí, že ležia v spoločnej premietacej rovine λ a v jej sklopení platí:
(k) ⊥( Isα)
●
≡Isα1
k1≡Isα1
●
Vajsáblová, M.: Deskriptívna geometria pre GaK 58

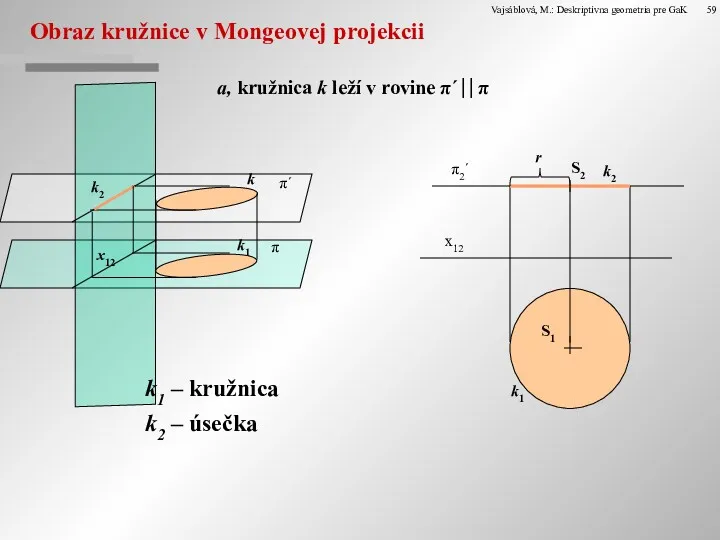
Obraz kružnice v Mongeovej projekcii
a, kružnica k leží v rovine π´⎥⎥ π
π
π´
π2´
x12
k2
k1
r
S2
S1
x12
k2
k1
k1 – kružnica
k2 – úsečka
k
Vajsáblová, M.: Deskriptívna geometria pre GaK 59

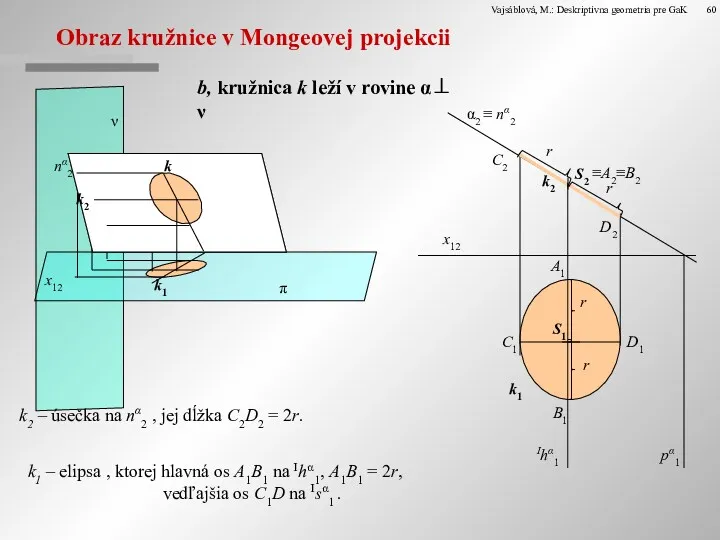
Obraz kružnice v Mongeovej projekcii
b, kružnica k leží v rovine α⊥ ν
π
α2 ≡ nα2
x12
k1
r
S2
S1
k2
k1
k2 – úsečka na nα2 , jej dĺžka C2D2 = 2r.
pα1
C2
D2
C1
D1
B1
A1
k1 – elipsa , ktorej hlavná os A1B1 na Ihα1, A1B1 = 2r,
vedľajšia os C1D na Isα1 .
≡A2≡B2
r
r
nα2
r
ν
Ihα1
k2
x12
k
Vajsáblová, M.: Deskriptívna geometria pre GaK 60

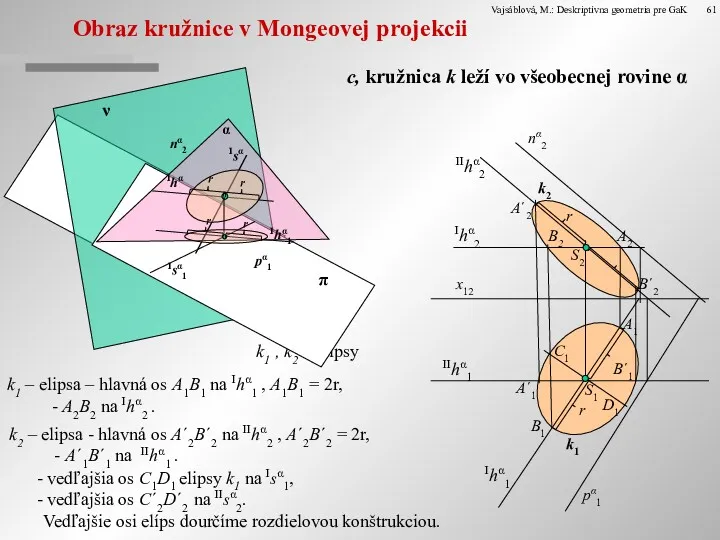
Obraz kružnice v Mongeovej projekcii
c, kružnica k leží vo všeobecnej rovine α
nα2
x12
r
S2
S1
k2
k1
k1 , k2 – elipsy
pα1
B´2
C1
D1
B1
A1
k1 – elipsa – hlavná os A1B1 na Ihα1 , A1B1 = 2r,
- A2B2 na Ihα2 .
B2
r
A2
A´2
A´1
k2 – elipsa - hlavná os A´2B´2 na IIhα2 , A´2B´2 = 2r,
- A´1B´1 na IIhα1 .
Ihα1
Ihα2
IIhα2
IIhα1
vedľajšia os C1D1 elipsy k1 na Isα1,
vedľajšia os C´2D´2 na IIsα2.
Vedľajšie osi elíps dourčíme rozdielovou konštrukciou.
B´1
π
ν
α
pα1
nα2
Ihα
Isα
Ihα1
Isα1
r
r
r
r
Vajsáblová, M.: Deskriptívna geometria pre GaK 61