Слайд 2

Нелинейные уравнения:
алгебраические (содержащие только алгебраические функции (целые, рациональные, иррациональные)
трансцендентные (содержащие другие
функции (тригонометрические, показа- показательные, логарифмические и др.)).
Слайд 3

1. Метод деления отрезка пополам (метод бисекции).
Пусть мы нашли отрезок
, на котором функция меняет знак , т.е. на котором находится значение корня , т. е.
В качестве начального приближения корня принимаем середину этого отрезка:
Слайд 4

Далее исследуем значения функции на концах отрезков и
Тот из отрезков,
на концах которого принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка .
Слайд 5
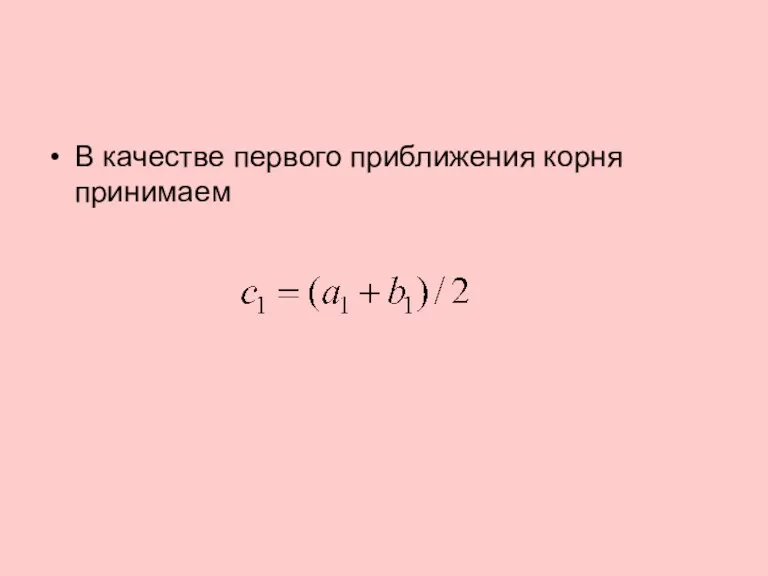
В качестве первого приближения корня принимаем
Слайд 6

Таким образом, k-е приближение вычисляется как
Слайд 7
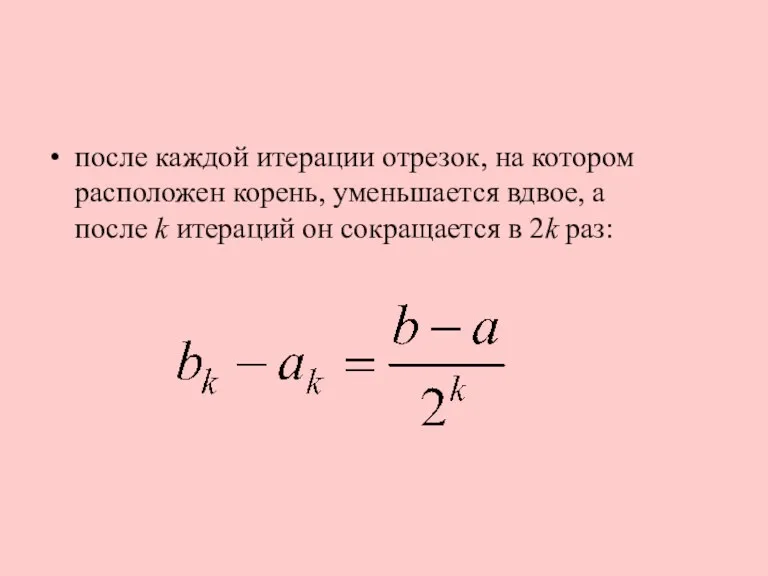
после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а
после k итераций он сокращается в 2k раз:
Слайд 8

Пусть приближенное решение требуется найти с точностью до некоторого заданного малого
числа :
Взяв в качестве приближенного решения k-е приближение корня: , учитывая, что
получим
Слайд 9

Последнее неравенство выполнено, если
Слайд 10

Слайд 11

метод деления отрезка пополам всегда сходится, причем можно гарантировать, что полученное
решение будет иметь любую наперед заданную точность.
Слайд 12

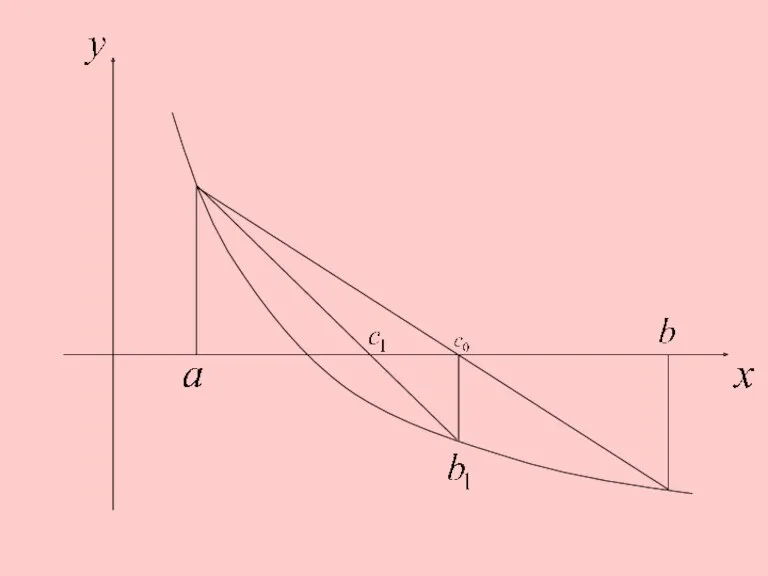
2. Метод хорд.
Процесс итераций состоит в том, что в качестве
приближений корню уравнения принимаются значения точек пересечения хорды с осью абсцисс.
( Для определенности примем )
Слайд 13

Сначала находим уравнение хорды ab:
Слайд 14

Для точки пересечения ее с осью абсцисс получим уравнение
Слайд 15

Далее, сравнивая знаки величин и для рассматриваемого случая, приходим к выводу,
что корень находится в интервале так как
. Отрезок отбрасываем.
и т.д.
Слайд 16

В качестве условия окончания итераций используется условие близости двух последовательных приближений
Слайд 17
Слайд 18

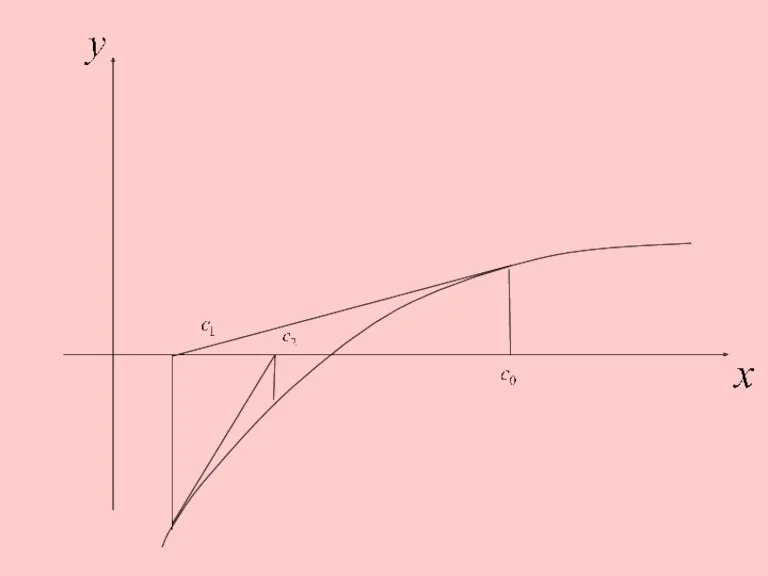
3. Метод Ньютона (метод касательных).
метод состоит в том, что на
k-й итерации проводится касательная к кривой у = F(x) и ищется точка пересечения касательной с осью абсцисс.
Слайд 19

При этом не обязательно задавать отрезок , содержащий корень уравнения, а
достаточно лишь найти некоторое начальное приближение корня
Слайд 20

Уравнение касательной, проведенной к кривой в точке имеет вид
Слайд 21

Отсюда найдем следующее приближение корня как абсциссу точки пересечения касательной с
осью х (у = 0):
Слайд 22

Аналогично формула для k-го приближения имеет вид
необходимо, чтобы не равнялась
нулю.
Слайд 23
Слайд 24

для погрешности корня имеет место соотношение
Слайд 25

4. Метод простой итерации.
Для использования этого метода исход- исходное нелинейное
уравнение записывается в виде
Слайд 26

Пусть известно начальное приближение корня
Подставляя это значение в правую часть
уравнения получаем новое приближение
Слайд 27

Подставляя каждый раз новое значение корня в уравнение получаем последовательность значений



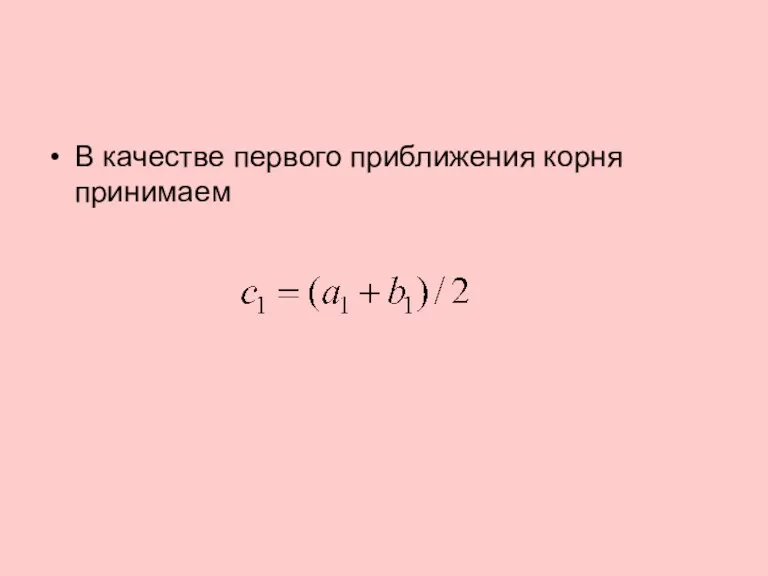

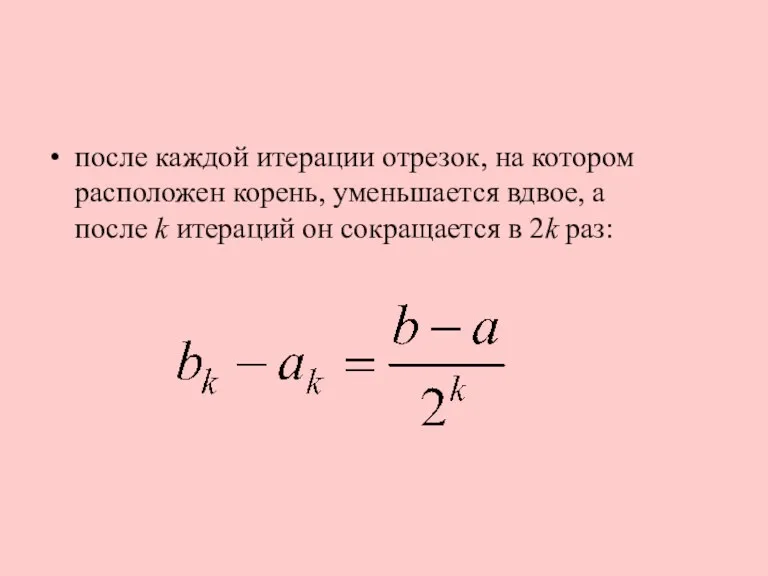




















 Уравнение линии
Уравнение линии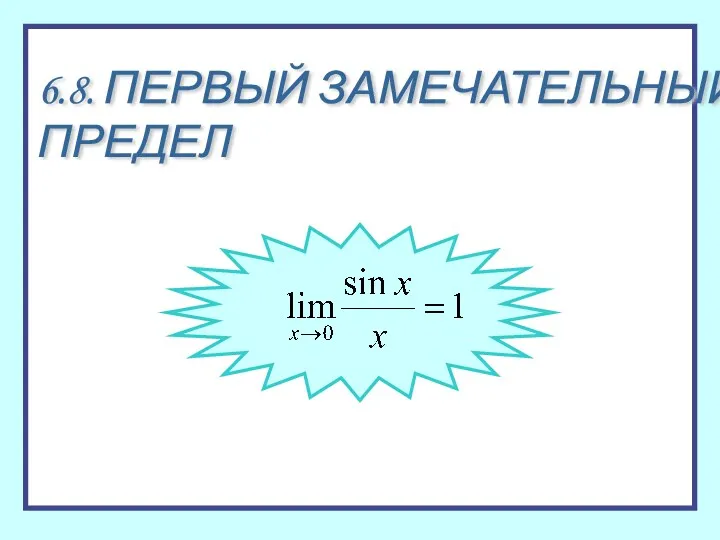 Первый замечательный предел
Первый замечательный предел Математика. 1 класс. Урок 62. Решение задач - Презентация
Математика. 1 класс. Урок 62. Решение задач - Презентация Среднее арифметическое
Среднее арифметическое Математическая викторина
Математическая викторина Перпендикулярные прямые
Перпендикулярные прямые 20231106_fomina_23
20231106_fomina_23 Значения синуса, косинуса и тангенса для углов 300, 600, 450 градусов
Значения синуса, косинуса и тангенса для углов 300, 600, 450 градусов Тренажёр по математике Листопад 1 класс по теме: Сложение и вычитание в пределах 5.
Тренажёр по математике Листопад 1 класс по теме: Сложение и вычитание в пределах 5. Циклический алгоритм на QBASIC. Циклы с предусловием и постусловием
Циклический алгоритм на QBASIC. Циклы с предусловием и постусловием Измерение отрезков
Измерение отрезков Тела вращения. 11 класс
Тела вращения. 11 класс Статистическое изучение динамики социально-экономических явлений и процессов
Статистическое изучение динамики социально-экономических явлений и процессов Measuring Inequality. An examination of the purpose and techniques of inequality measurement
Measuring Inequality. An examination of the purpose and techniques of inequality measurement Деление дробей
Деление дробей Мастер-класс по внеурочной деятельности. Нестандартный способ запоминания таблицы умножения.
Мастер-класс по внеурочной деятельности. Нестандартный способ запоминания таблицы умножения. Задания для подготовки к контрольной работе
Задания для подготовки к контрольной работе Деление обыкновенных дробей
Деление обыкновенных дробей Методы исследования потоков и аппаратов
Методы исследования потоков и аппаратов Презентация к работе Числа в пословицах и поговорках
Презентация к работе Числа в пословицах и поговорках Педагогические условия повышения уровня подготовки учащихся к ОГЭ по математике
Педагогические условия повышения уровня подготовки учащихся к ОГЭ по математике Урок 39. Сумма и произведение. Знак умножения.
Урок 39. Сумма и произведение. Знак умножения. Деление обыкновенных дробей
Деление обыкновенных дробей Задания С2 на ЕГЭ. Координатный метод. Координаты многогранников
Задания С2 на ЕГЭ. Координатный метод. Координаты многогранников 20231022_konus
20231022_konus Векторы в пространстве
Векторы в пространстве Транспортная задача линейного программирования
Транспортная задача линейного программирования конкурс по математике Эврика
конкурс по математике Эврика