Содержание
- 2. Опр. 1 Функция F(x), определенная на интервале ( a, b), называется первообразной для f ( x
- 3. Основные свойства неопределенного интеграла
- 4. Таблица интегралов
- 5. Методы интегрирования 1. Табличное интегрирование 2. Метод подведения под знак дифференциала (подстановки) ТЕОРЕМА 2. Пусть требуется
- 6. Замена переменной Интегрирование квадратных трехчленов
- 7. 3. Интегрирование по частям ТЕОРЕМА 3. Пусть U(x) и V(x) две дифференцируемые функции Тогда I. II.
- 8. 4. Интегрирование рациональных дробей ОПР. 3 Рациональной дробью (дробно-рациональной функцией) называется частное от деления двух целых
- 9. Теорема 6. Если среди корней есть мнимые, то они обязательно сопряженные и множитель, за счет которого
- 10. ТЕОРЕМА 7. Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа элементарных дробей,
- 11. Порядок действий при вычислении интеграла от рационального выражения Выделить целую часть (сделать дробь Q(x)/P(x) правильной) Разложить
- 12. 5. Интегрирование тригонометрических выражений Будем использовать запись интеграла от тригонометрических выражений это означает, что над синусом
- 13. Более простые методы используются в следующих случаях: Следует использовать формулы: 2. Интегралы вида а) n –
- 14. а) подынтегральная функция нечетна относительно синуса Рекомендуемая подстановка: cos x = t б) подынтегральная функция нечетна
- 15. а) Рекомендуемая подстановка б) применить формулы 4. Интегралы вида
- 16. 6. Интегрирование иррациональных выражений Рекомендуемая подстановка: Выделить полный квадрат в
- 17. α, β, γ …– дробные рациональные числа, s – наименьшее общее кратное α, β, γ α,
- 18. 5. Дифференциальный бином ОПР. 5 Выражение вида , где (m,n,p,a,b) – const, называется дифференциальным биномом. Теорема
- 20. Скачать презентацию

















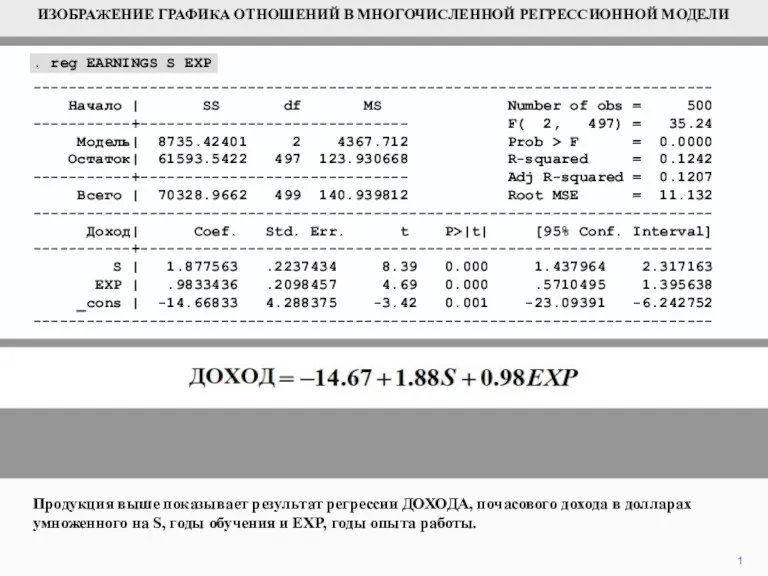 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели Последовательность. Лингво–математический урок
Последовательность. Лингво–математический урок Подготовка учащихся к ОГЭ по математике
Подготовка учащихся к ОГЭ по математике Цилиндр, конус и шар
Цилиндр, конус и шар Движение по окружности
Движение по окружности Сумма углов треугольника
Сумма углов треугольника ГИА - 2012. Открытый банк заданий по математике. (Задача 4)
ГИА - 2012. Открытый банк заданий по математике. (Задача 4) Создание тренажера по подготовке к ОГЭ по математике
Создание тренажера по подготовке к ОГЭ по математике Центральные и вписанные углы
Центральные и вписанные углы Правильные многогранники
Правильные многогранники Элективный курс. Фигурные числа. (5-7 класс)
Элективный курс. Фигурные числа. (5-7 класс) Число и цифра 7.
Число и цифра 7. Активизация познавательной деятельности учащихся на уроках математики
Активизация познавательной деятельности учащихся на уроках математики Степени и корни
Степени и корни Полуплоскость. Луч. Прямая
Полуплоскость. Луч. Прямая Два замечательных предела
Два замечательных предела Рациональные неравенства. Задания для устного счета
Рациональные неравенства. Задания для устного счета Длина окружности (6 класс)
Длина окружности (6 класс)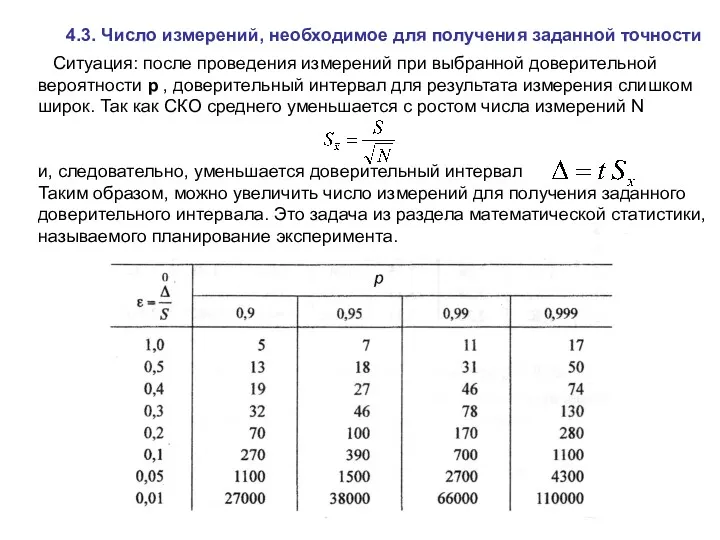 Число измерений, необходимое для получения заданной точности
Число измерений, необходимое для получения заданной точности Математическая игра Звездный час
Математическая игра Звездный час Основы математики
Основы математики The circle, the circumference and their elements. The central angle
The circle, the circumference and their elements. The central angle Положительные и отрицательные числа вокруг нас
Положительные и отрицательные числа вокруг нас Движение. Урок математики в 4 классе
Движение. Урок математики в 4 классе Обобщение по теме Четырехугольники. 8 класс
Обобщение по теме Четырехугольники. 8 класс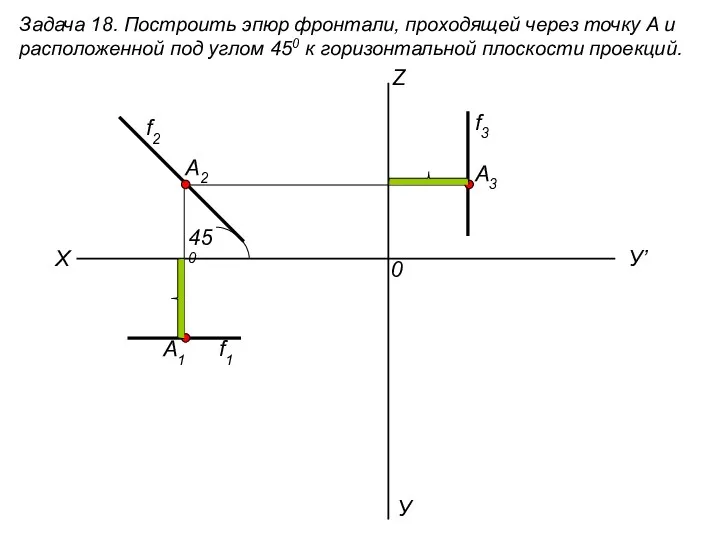 Построить эпюр фронтали, проходящей через точку А и расположенной под углом 450 к горизонтальной плоскости проекций. (задача 18)
Построить эпюр фронтали, проходящей через точку А и расположенной под углом 450 к горизонтальной плоскости проекций. (задача 18) методическая разработка урока математики Единицы времени.Век
методическая разработка урока математики Единицы времени.Век Статистические методы проверки гипотез
Статистические методы проверки гипотез