Содержание
- 2. §1. Первообразная функции. Неопределенный интеграл и его свойства. Таблица основных неопределенных интегралов. В дифференциальном исчислении решается
- 3. Определение 1. Функция называется первообразной функции заданной на некотором множестве если для выполняется равенство
- 4. Пример. Пусть Тогда первообразной для данной функции является функция так как
- 5. Очевидно, что первообразными будут также любые функции где поскольку
- 6. Таким образом, если и − две первообразные одной и той же функции то
- 7. Определение 2. Множество всех первообразных функции на множестве называется неопределенным интегралом и обозначается
- 8. Здесь − знак интеграла, − подынтегральная функция, − подынтегральное выражение, − переменная интегрирования.
- 9. Нахождение первообразной для данной функции называется интегрированием функции Теорема. Для всякой непрерывной на функции существует на
- 10. Геометрически неопределенный интеграл представляет собой семейство кривых, зависящих от одного параметра которые получаются одна из другой
- 11. Перечислим основные свойства неопределенного интеграла: 1) 2) 3)
- 12. 4) 5) Если то где − произвольная функция, имеющая непрерывную производную.
- 13. 6) Если то для
- 14. Приведем таблицу основных неопределенных интегралов: 3) 2) 1)
- 15. 7) 6) 5) 4)
- 16. 11) 10) 9) 8)
- 17. 12) 15) 14) 13)
- 18. Приведенные в данной таблице интегралы называют табличными.
- 19. §2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ. 2.1. Метод непосредственного интегрирования. Непосредственным интегрированием называют интегрирование с помощью свойств 3,
- 20. Примеры. 1)
- 21. 2)
- 22. 3)
- 23. 4)
- 24. 5)
- 26. 6)
- 27. 7)
- 28. 8)
- 30. 2.2. Метод поднесения под знак дифференциала и замены переменной. На практике часто встречаются интегралы вида или
- 31. Подведем в этом интеграле множитель под знак дифференциала: а затем произведем подстановку В результате получим формулу
- 33. Следовательно, задача свелась к нахождению интеграла который либо уже табличный, либо легко сводится к табличному, и
- 34. Примеры поднесения под знак дифференциала:
- 41. Примеры. 1)
- 42. 2)
- 43. 3)
- 44. 4)
- 45. 5)
- 46. 6)
- 47. 7)
- 48. 8)
- 49. 9)
- 51. 2.3. Метод интегрирования по частям. Пусть и − дифференцируемые функции. Тогда справедлива следующая формула интегрирования по
- 52. С помощью этой формулы вычисление интеграла сводится к отысканию другого интеграла Применение формулы целесообразно в тех
- 53. При этом в качестве следует брать такую функцию, которая при дифференцировании упрощается, а в качестве −
- 54. 1. Интегралы вида
- 55. где − многочлен, − число. Удобно положить а соответственно.
- 56. Тогда формулу (2.1) надо применять столько раз, какова степень многочлена т.е. раз.
- 57. 2. Интегралы вида
- 59. В этом случае соответственно, а
- 60. 3. Интегралы вида Можно положить или
- 61. Примеры. 1)
- 64. 2)
- 66. 2.4. Интегрирование рациональных дробей. Определение. Рациональной дробью называется функция, заданная в виде отношения двух многочленов:
- 67. Если степень многочлена числителя меньше степени многочлена знаменателя, т.е. то рациональная дробь называется правильной; в противном
- 68. Простейшей дробью называется правильная дробь одного из следующих типов: 3. 2. 1.
- 69. 5. 4. где
- 70. 2.4.1. Интегрирование простейших рациональных дробей. Интегрирование простейших рациональных дробей рассмотрим на примерах.
- 71. Примеры. 1)
- 72. 2)
- 73. 3) Выделим в знаменателе последнего подынтегрального выражения полный квадрат.
- 74. Тогда
- 75. Вернемся к интегралу:
- 77. 4) В числителе подынтегрального выражения нужно получить производную знаменателя, т.е. Тогда
- 81. 2.4.2. Интегрирование рациональных дробей с помощью разложения их на простейшие дроби. Перед интегрированием рациональной дроби необходимо
- 82. 1. Если дана неправильная рациональная дробь, выделить из нее целую часть, разделив числитель на знаменатель столбиком,
- 83. 2. Разложить знаменатель дроби на линейные и квадратичные множители: где
- 84. 3. Правильную рациональную дробь разложить на сумму простейших дробей:
- 88. Примеры. 1)
- 89. Тогда
- 90. Итак,
- 92. 2)
- 100. 2.5. Интегрирование иррациональных функций. 2.5.1. Квадратичные иррациональности. I. Интегралы вида
- 101. (2.5)
- 103. Выделим в подкоренном выражении полный квадрат:
- 110. III. Интегралы вида где − рациональная функция, сводится к интегралу от рациональной функции с помощью подстановки
- 111. где
- 112. Пример.
- 115. IV. Интегралы вида где − рациональная функция, сводится к интегралу от рациональной функции с помощью подстановки
- 116. где
- 117. Пример.
- 120. IV. Интегралы вида где − рациональная функция, сводится к интегралу от рациональной функции с помощью подстановки
- 121. где
- 122. 2.6. Интегрирование тригонометрических выражений. I. Интегралы вида где − рациональная функция аргументов и рациональных функций с
- 123. В результате этой подстановки имеем
- 125. Универсальная подстановка во многих случаях приводит к сложным вычислениям, поэтому на практике применяют и другие, более
- 126. то применяется подстановка При этом используются формулы
- 127. 2. если − нечетная функция относительно т.е. то применяется подстановка
- 128. 3. если − нечетная функция относительно т.е. то применяется подстановка
- 129. II. Интегралы вида находят а) при нечетном с помощью подстановки б) при нечетном с помощью подстановки
- 130. в) если же и − четные, то подынтегральную функцию необходимо преобразовать с помощью формул тригонометрии:
- 132. Примеры. 1) Так, как для подынтегральной функции не выполняется ни одно из условий:
- 133. то будем применять универсальную тригонометрическую подстановку:
- 141. Скачать презентацию











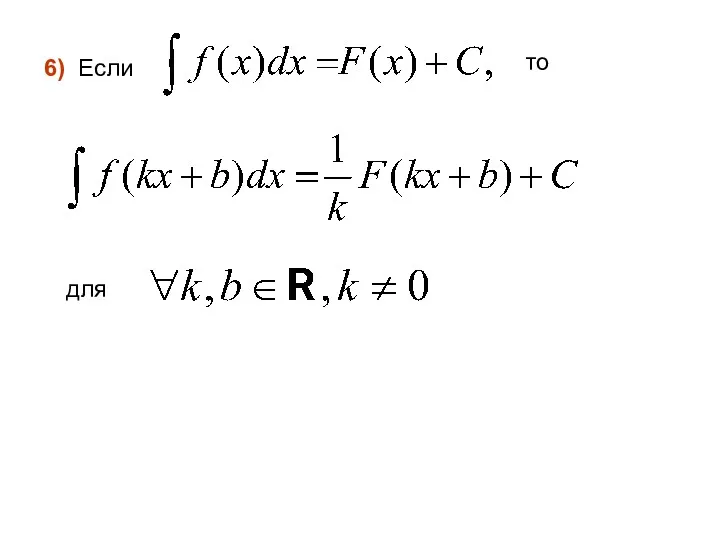

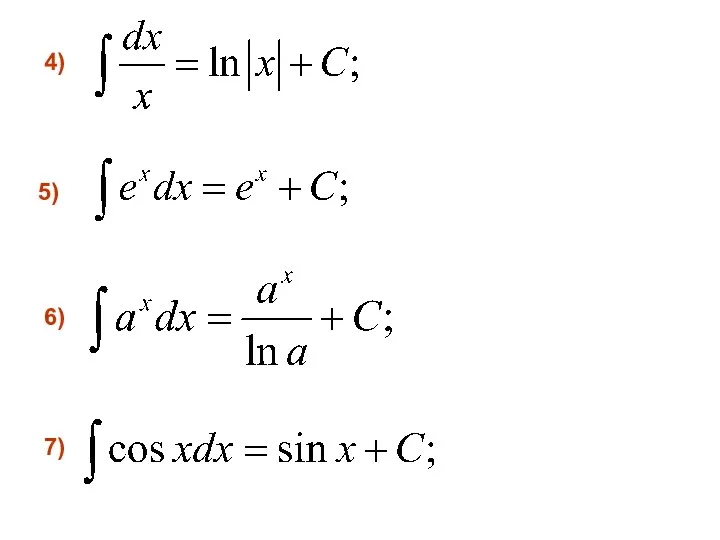
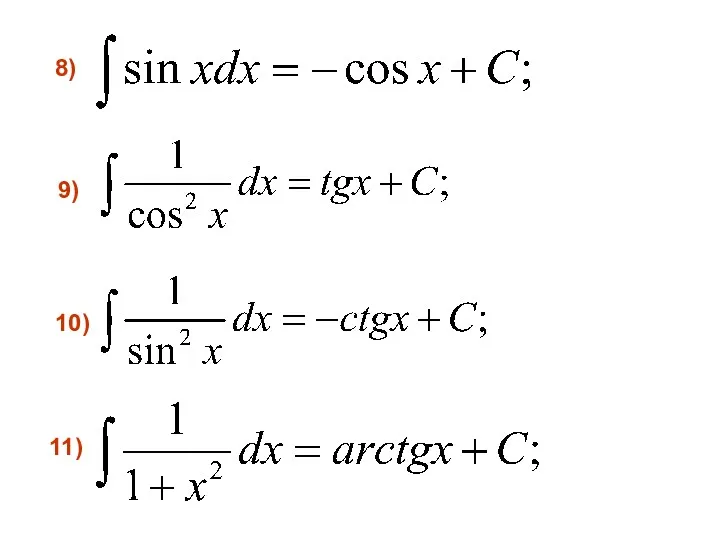
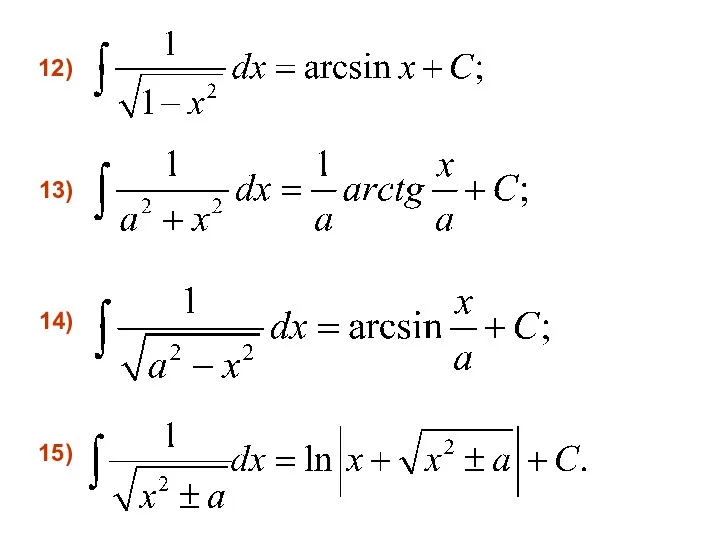


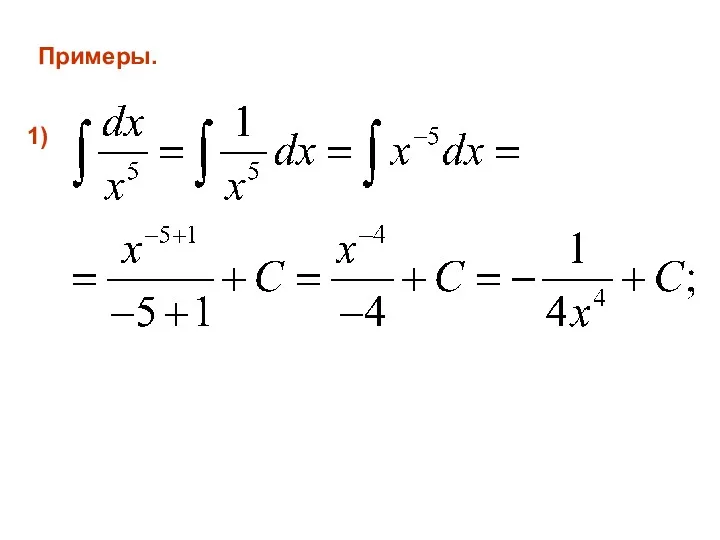
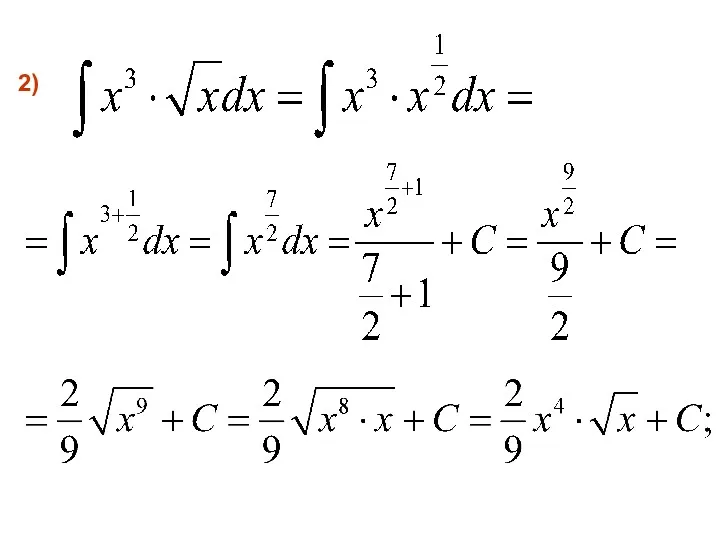
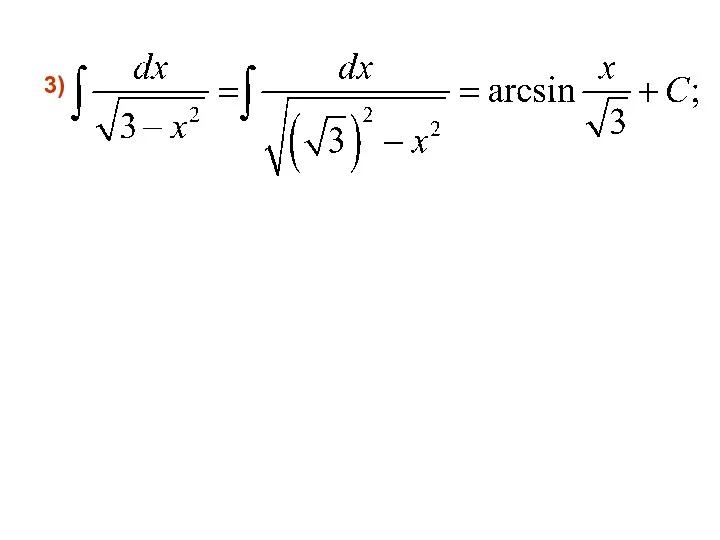
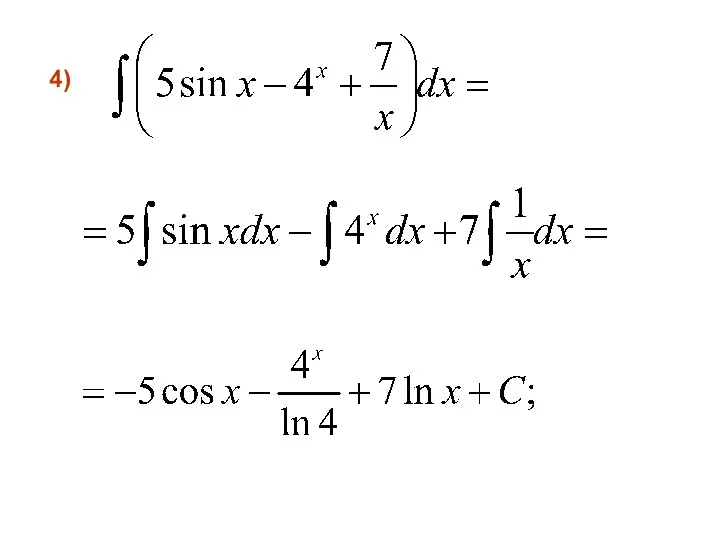
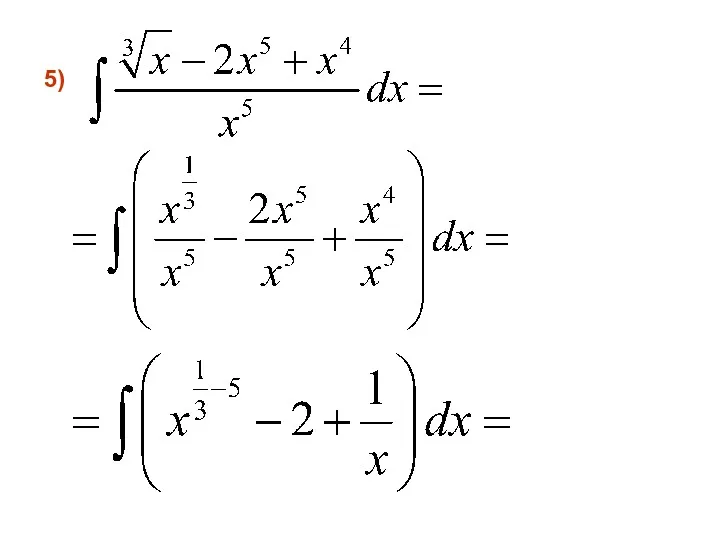
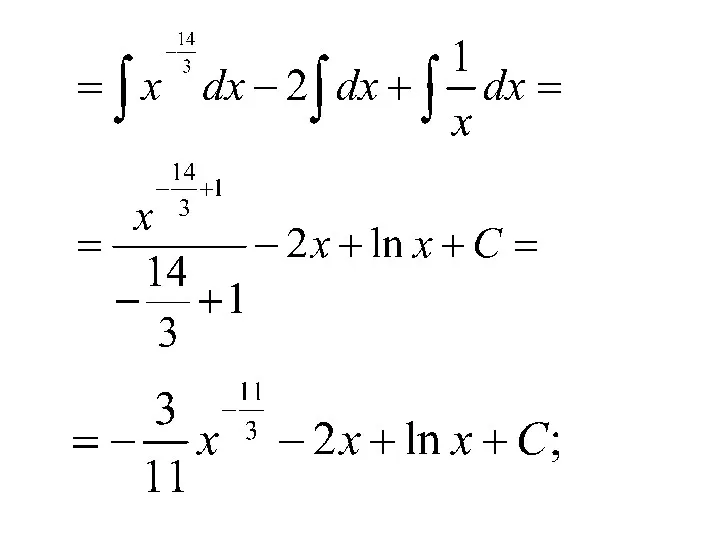
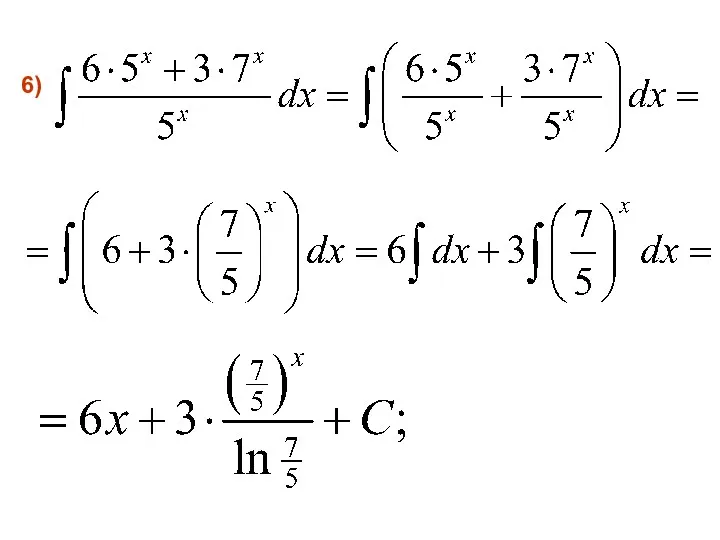
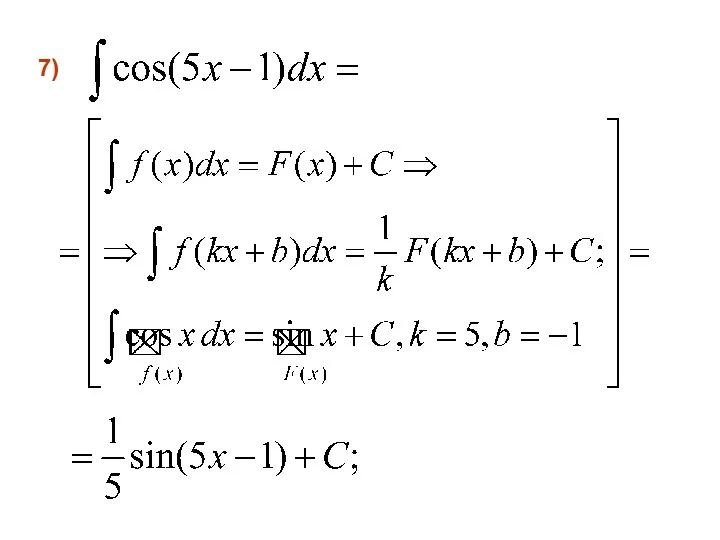
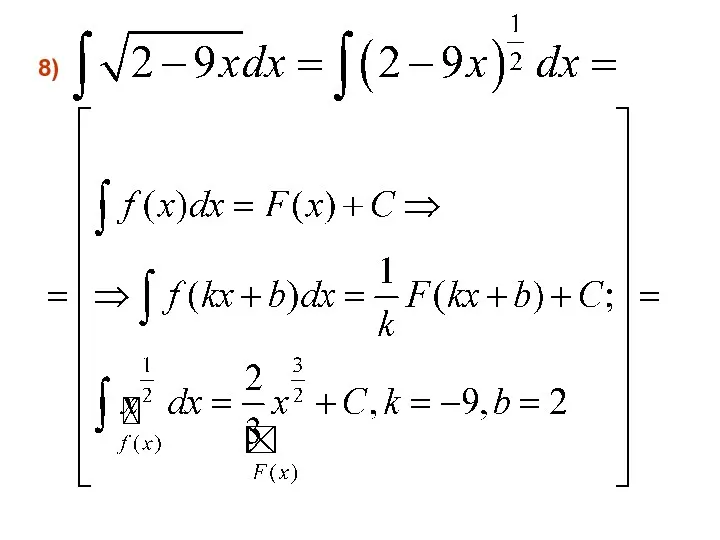
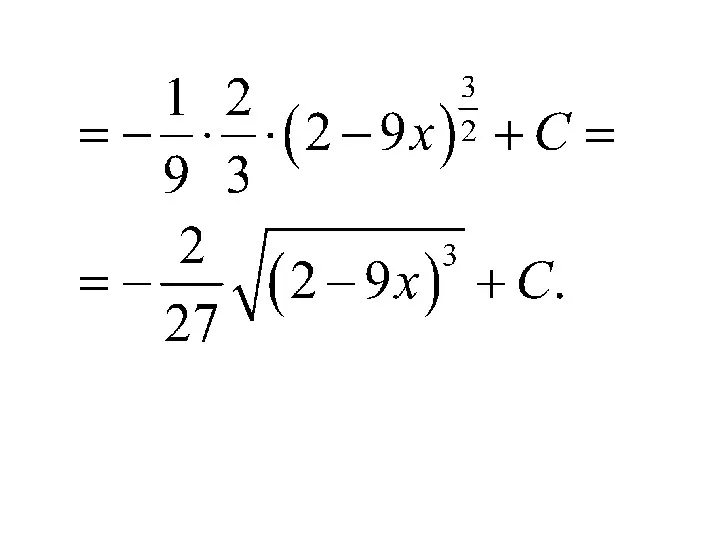


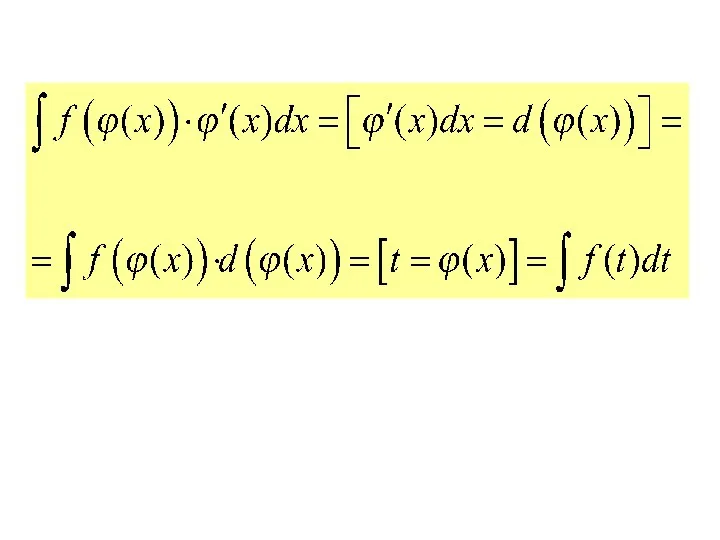


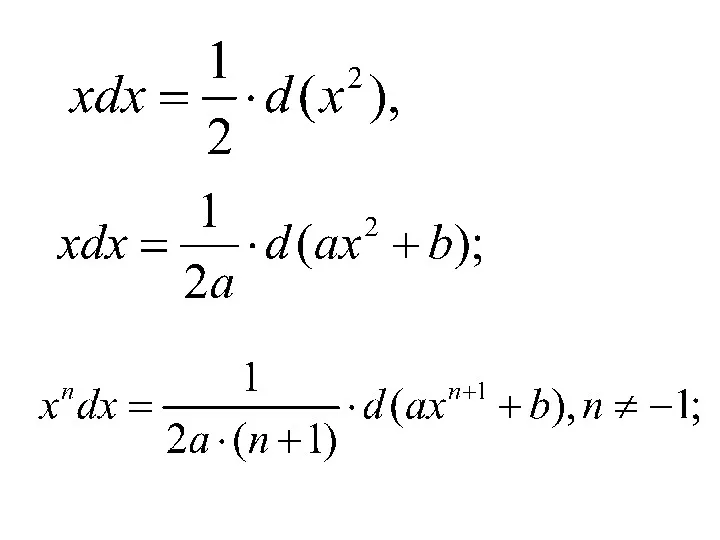
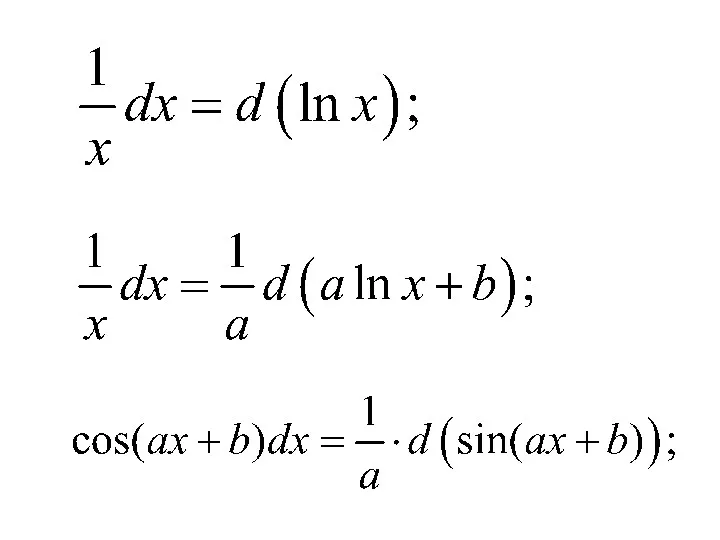
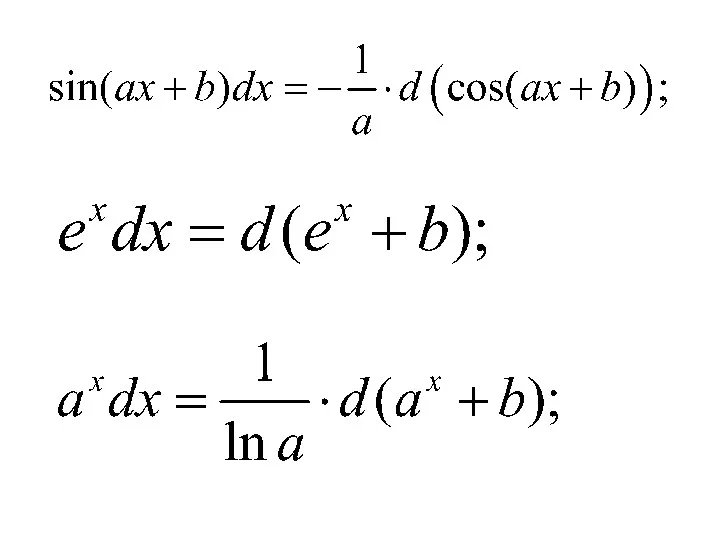
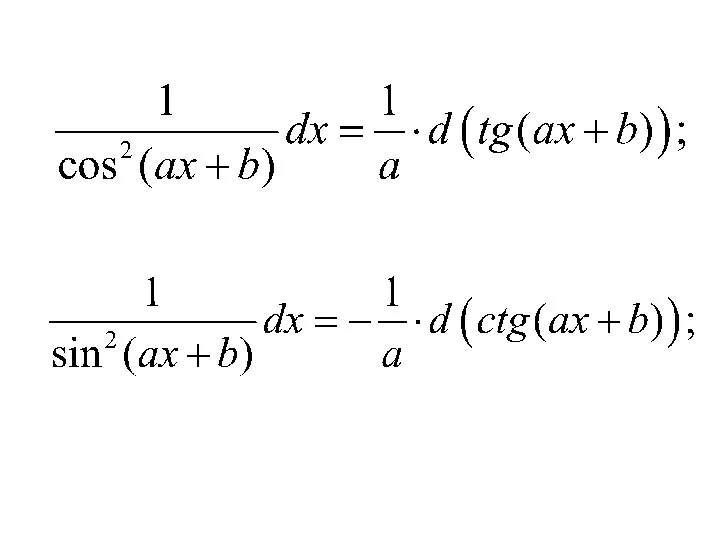
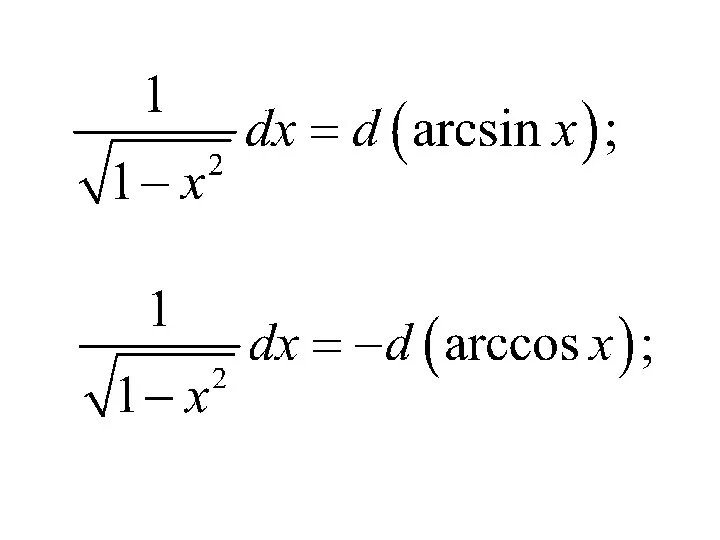
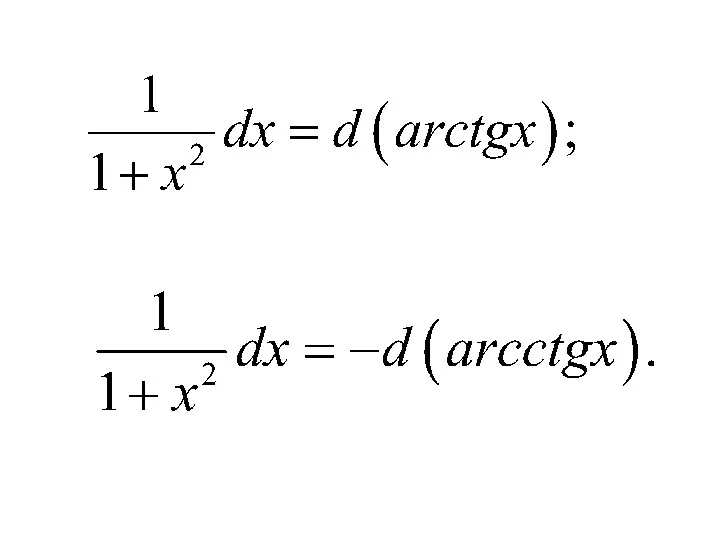
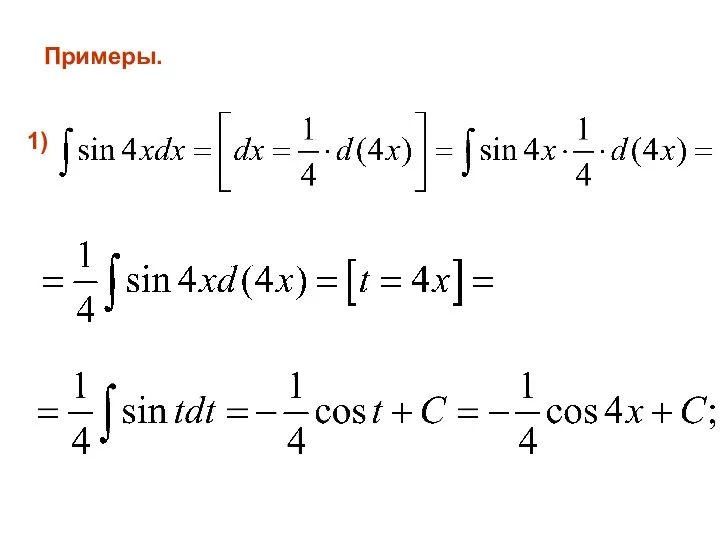
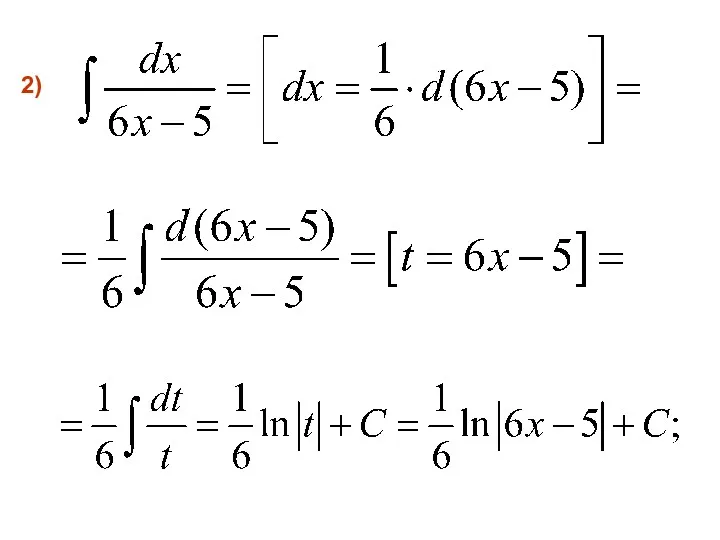
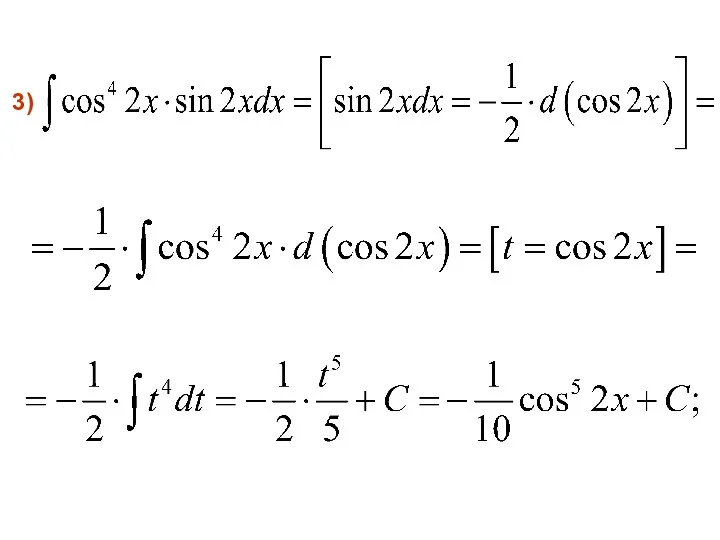
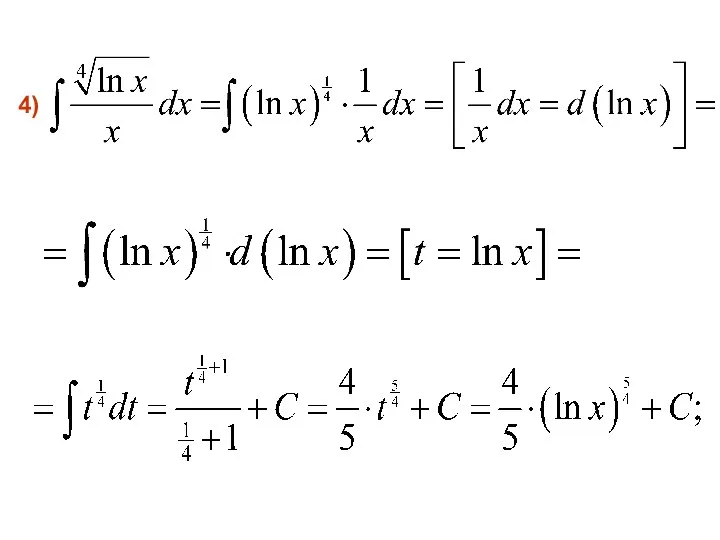
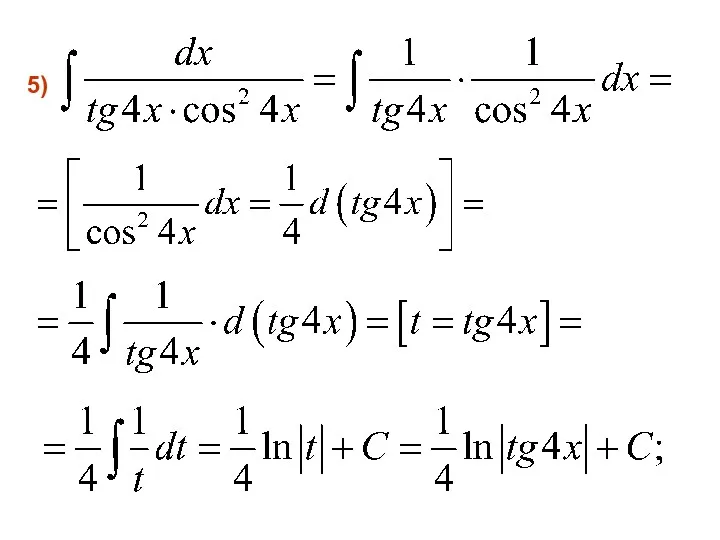

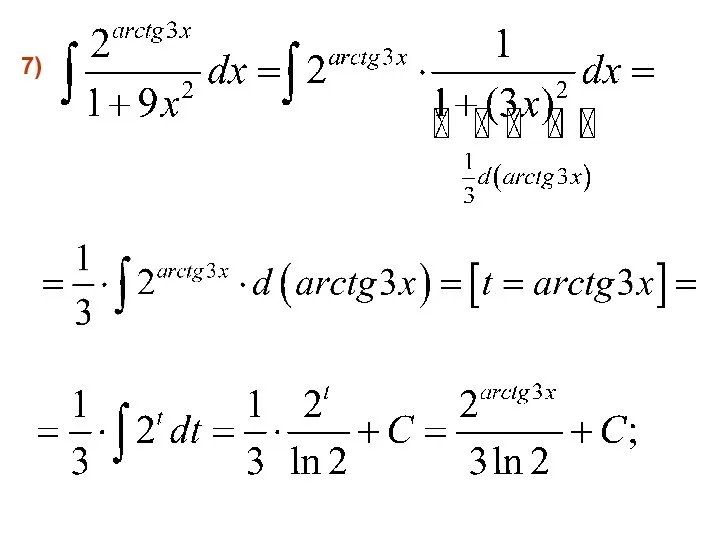
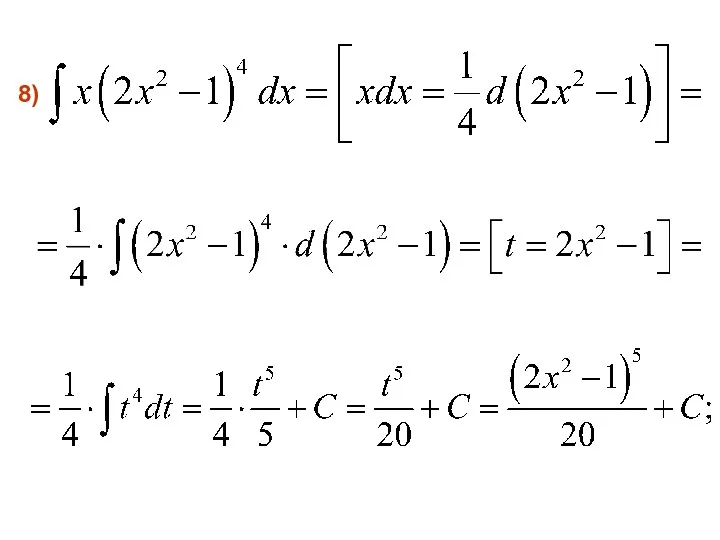
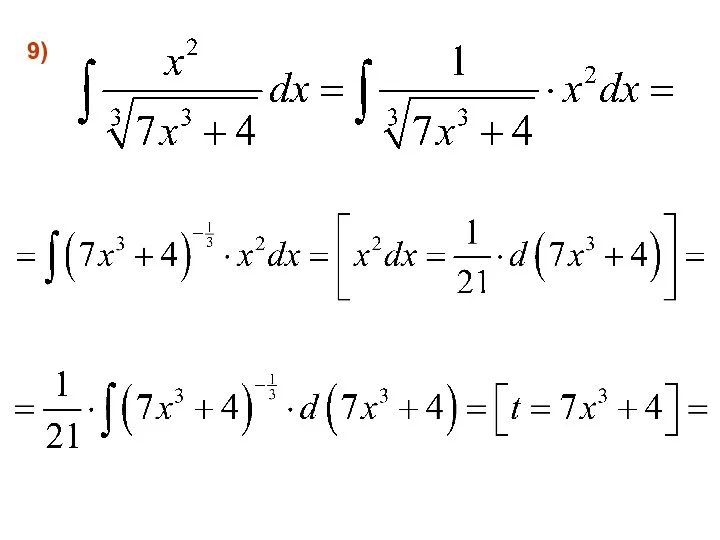
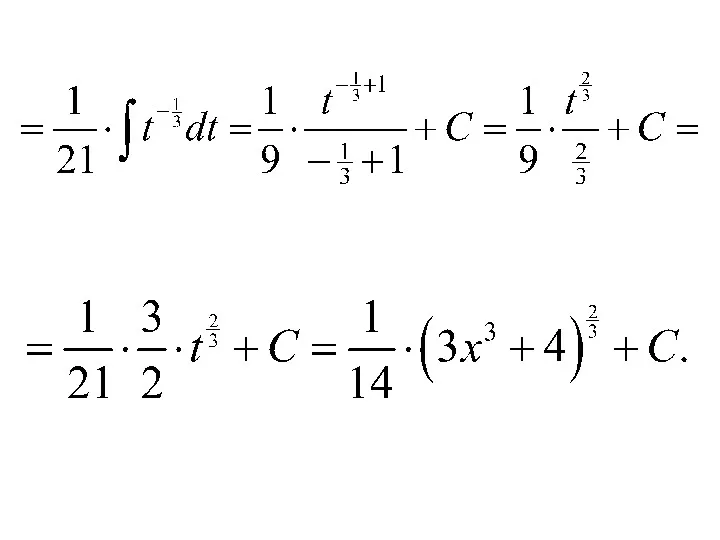




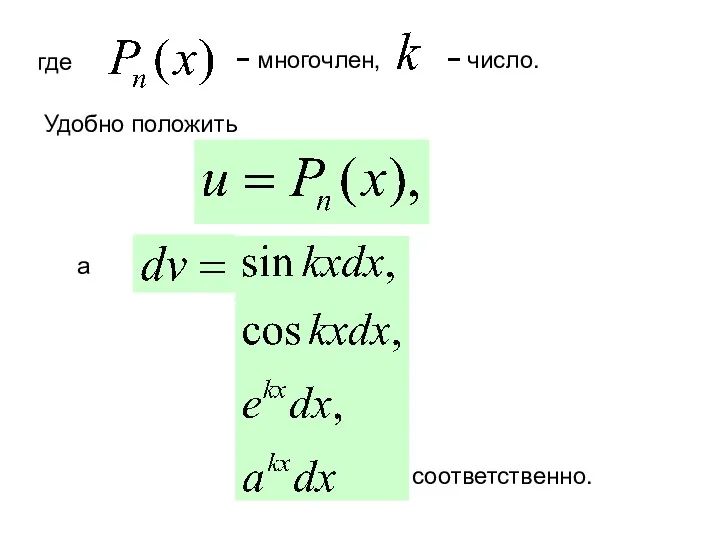





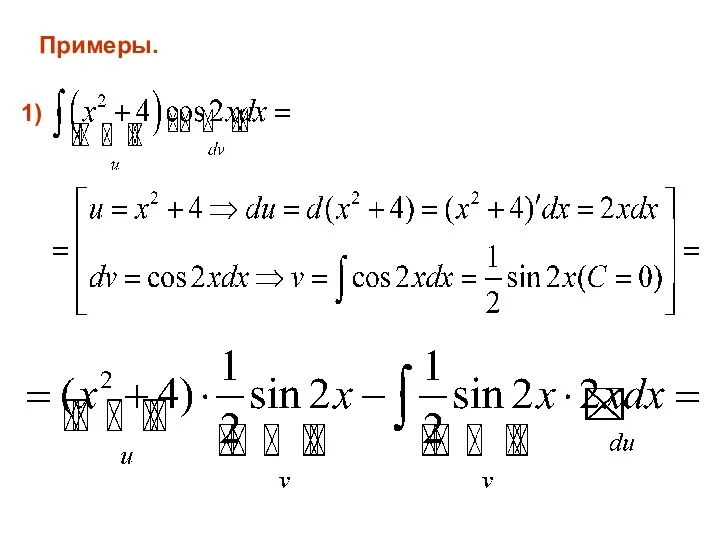
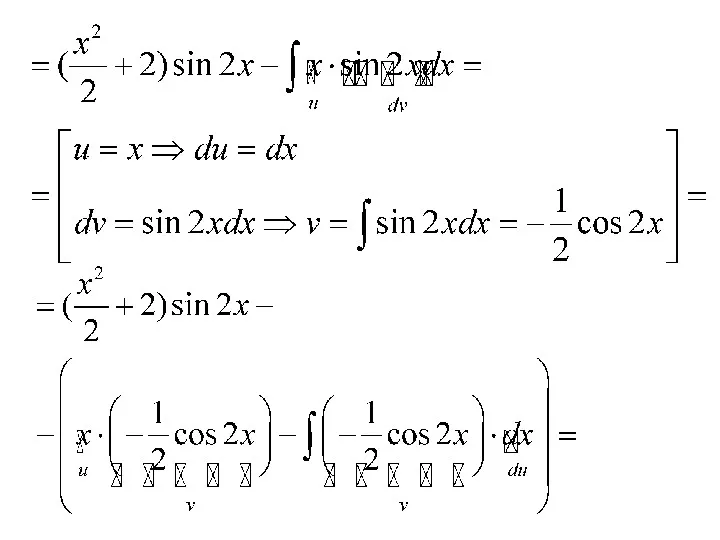
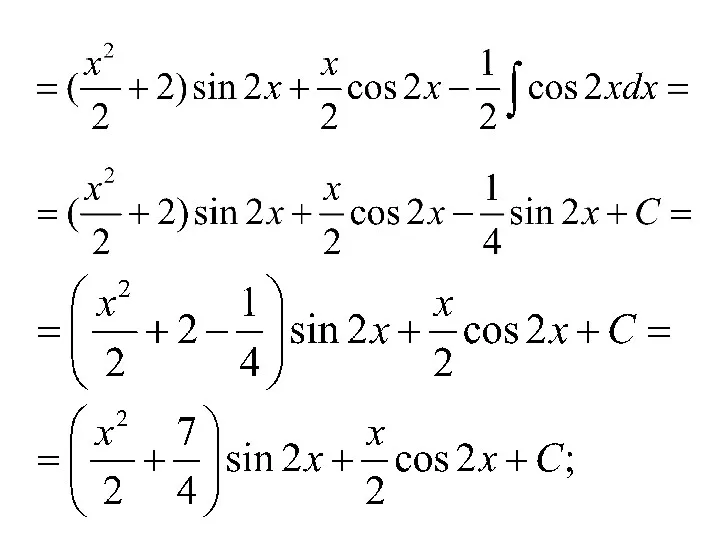
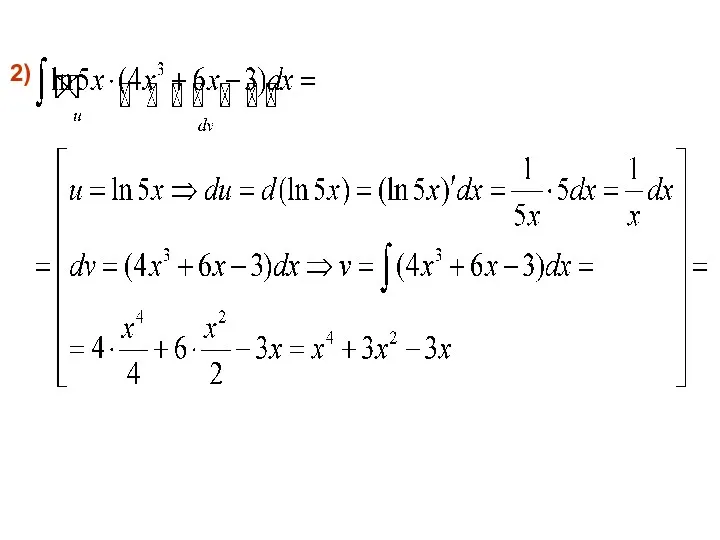




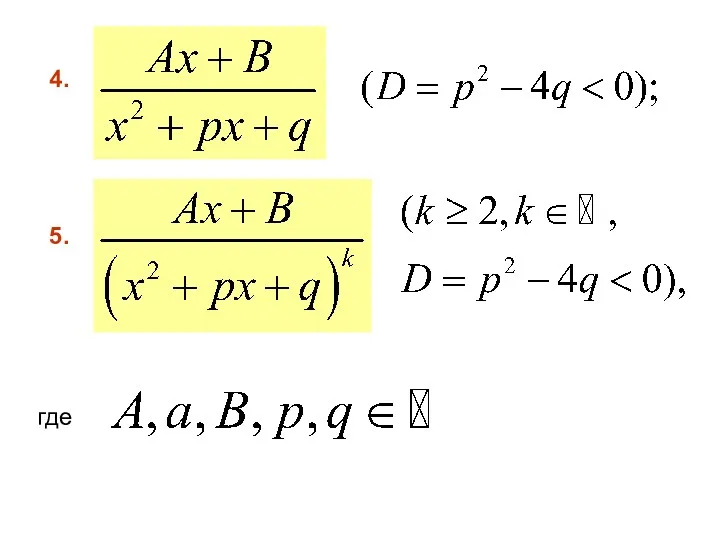

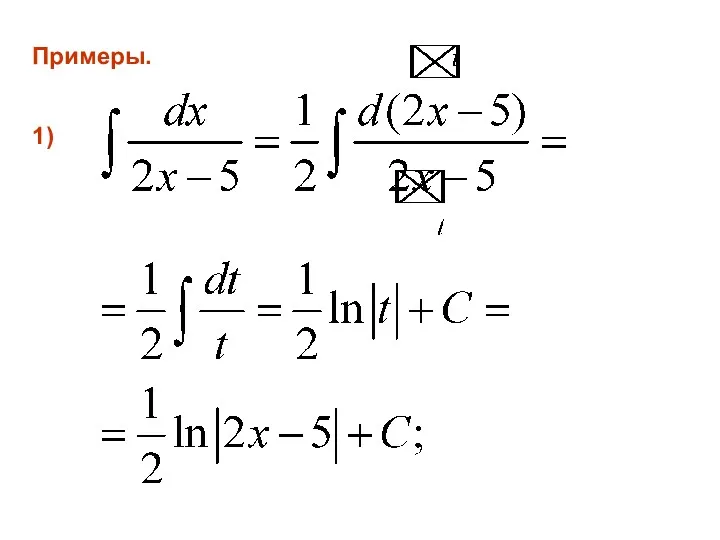
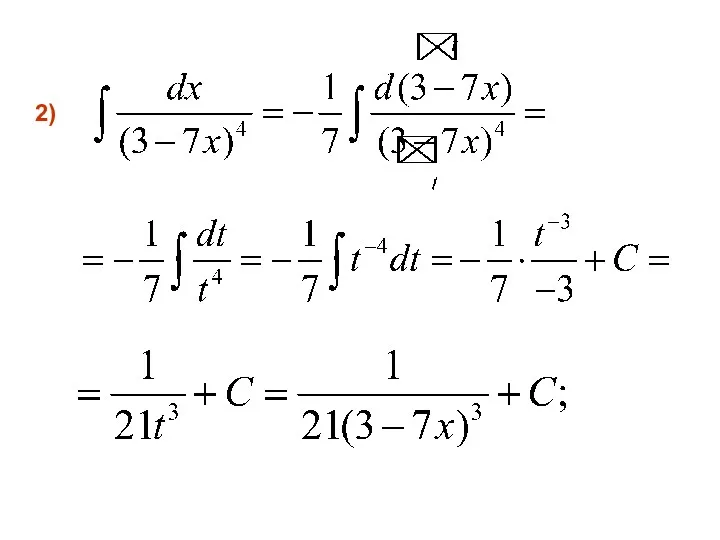

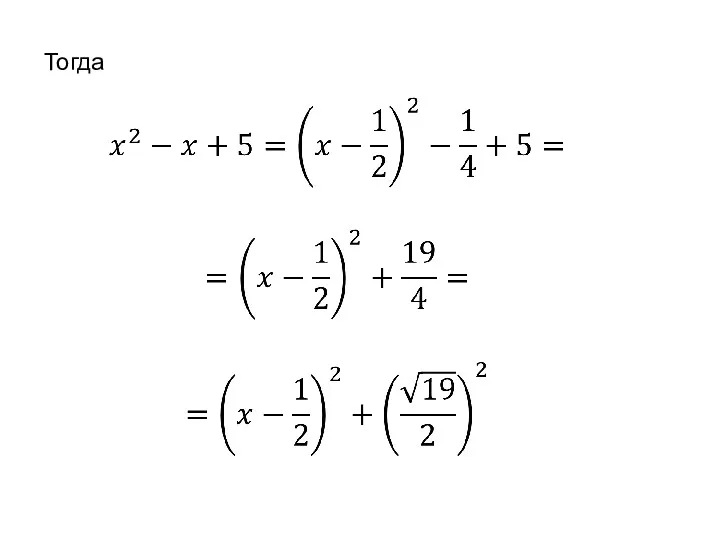
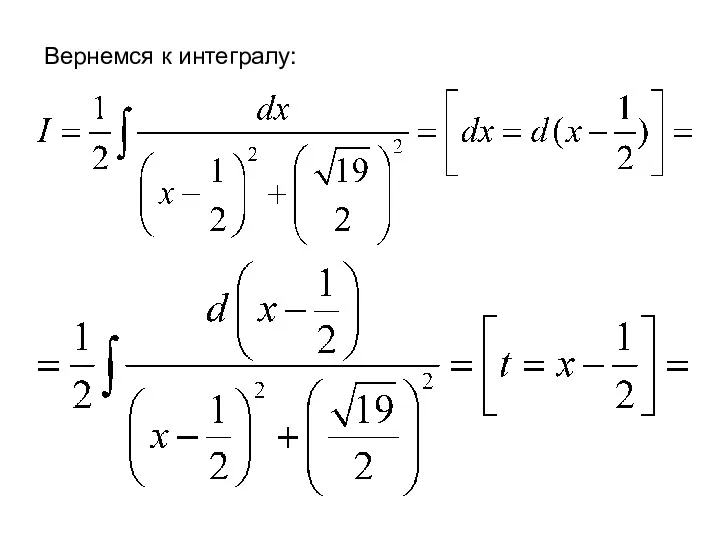
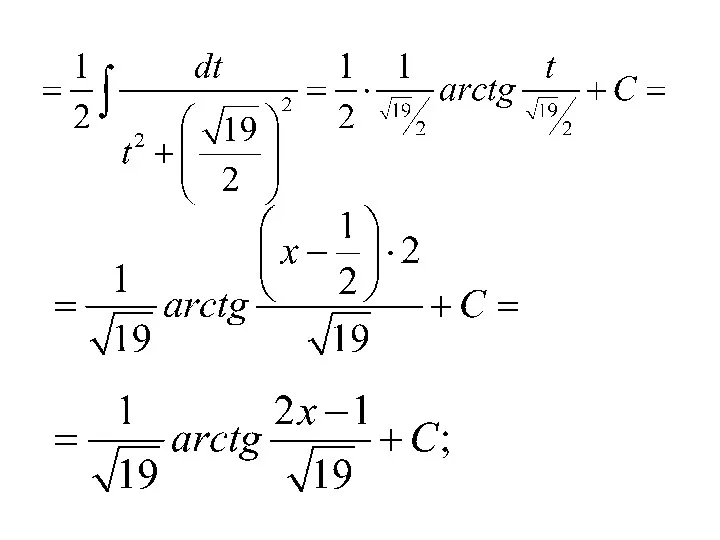

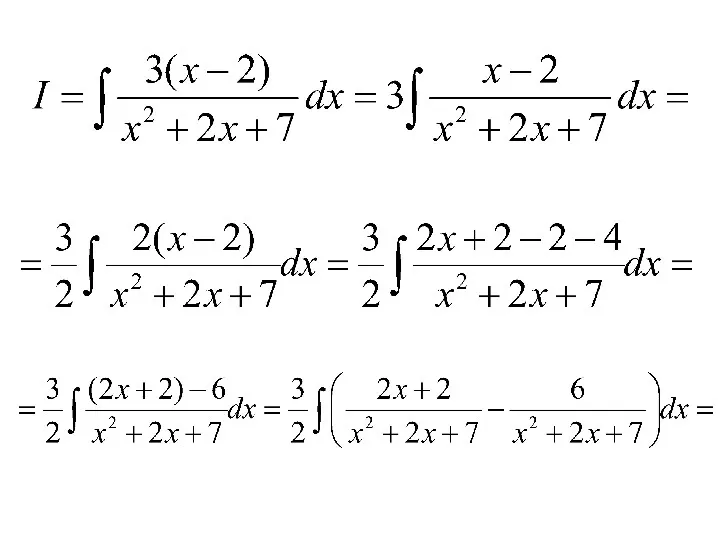

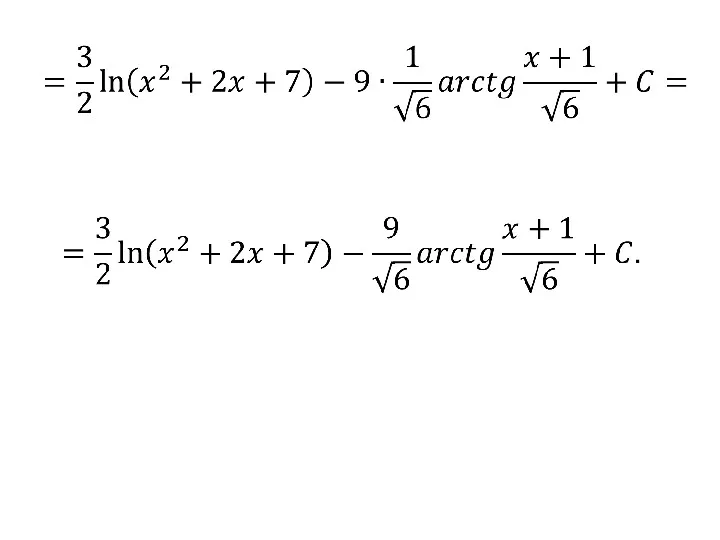








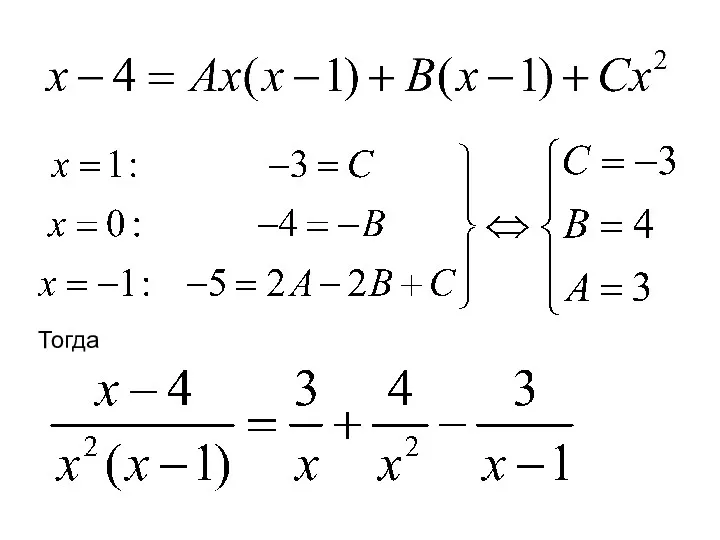
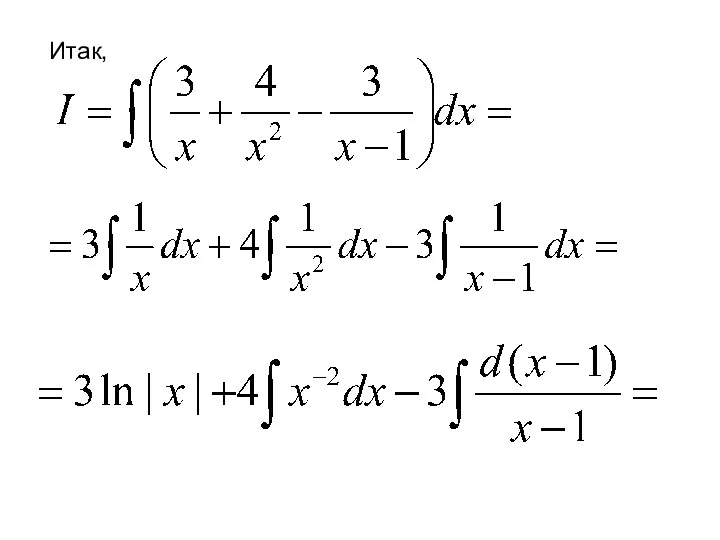
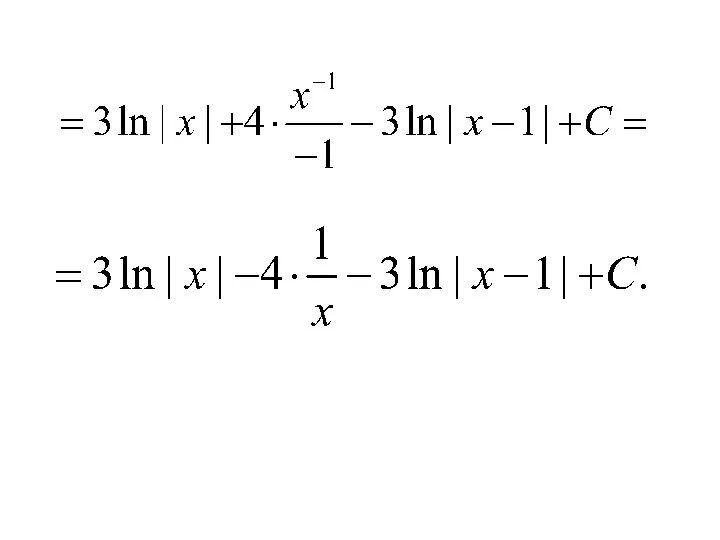
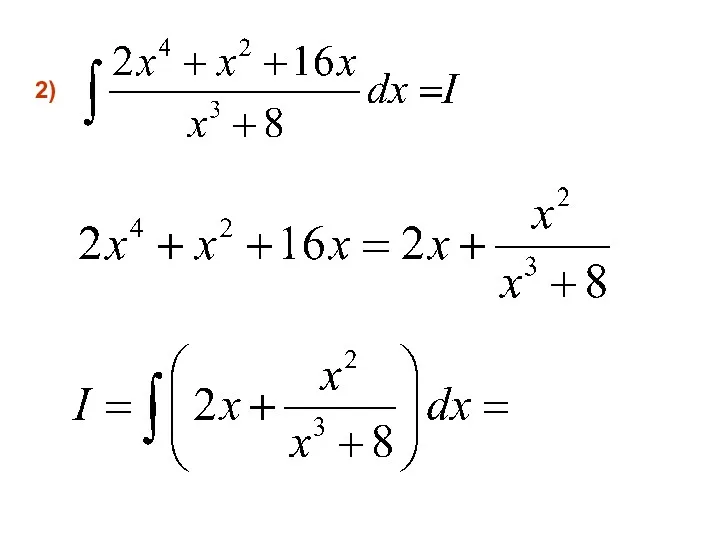

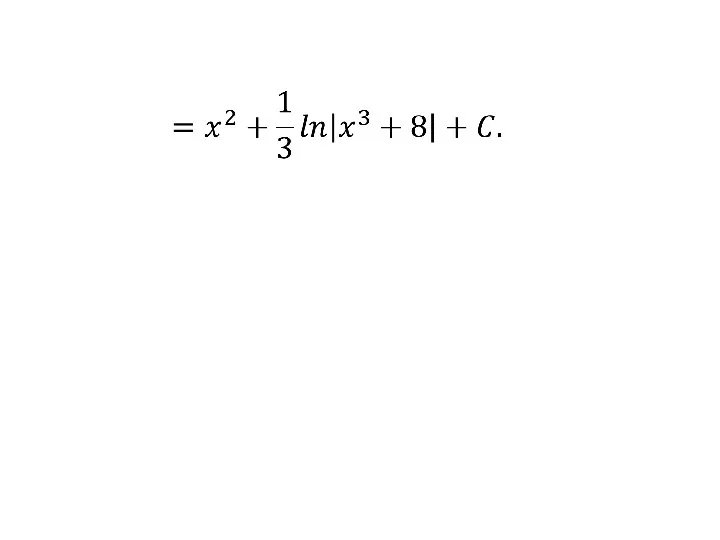
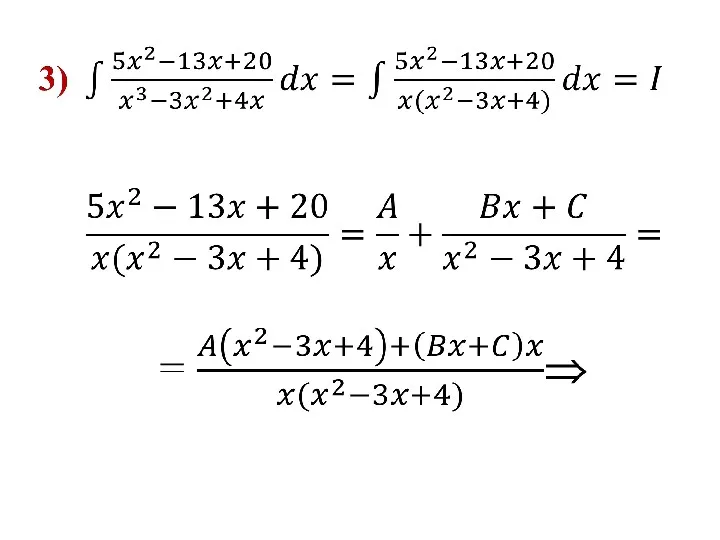
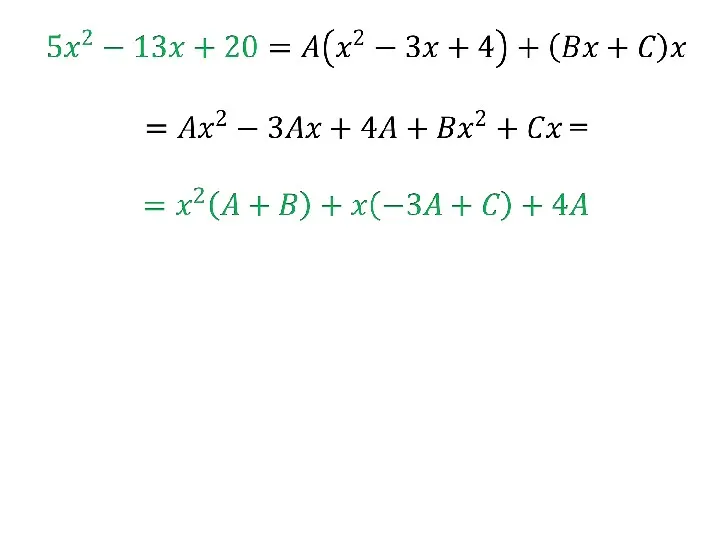


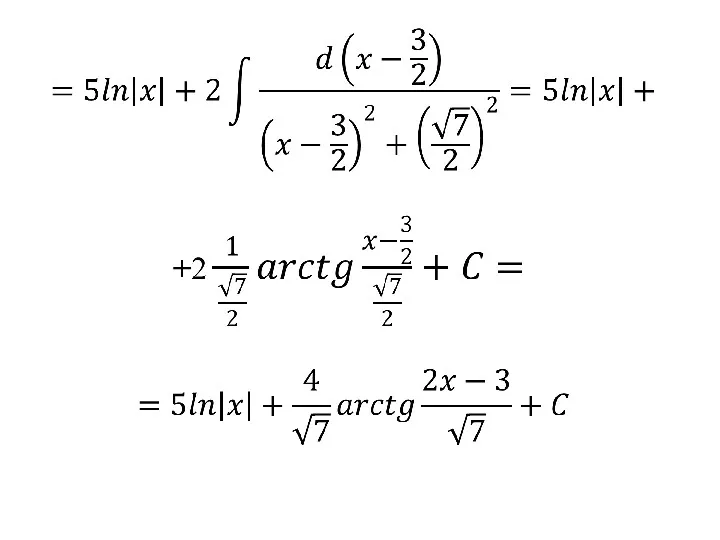


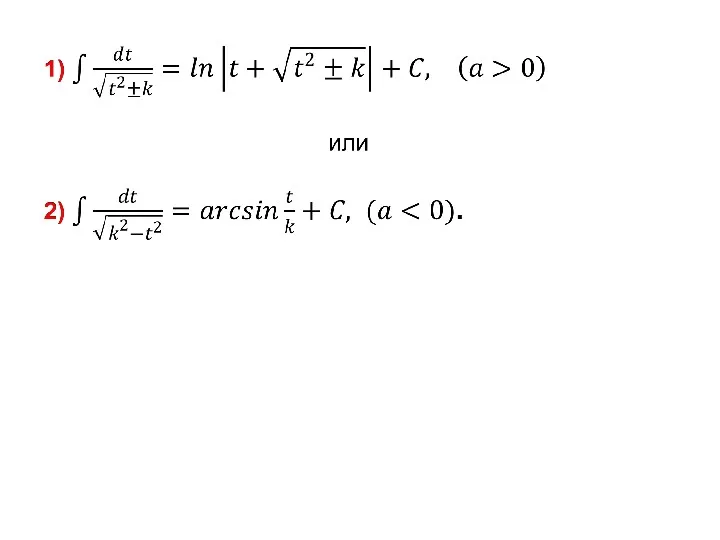




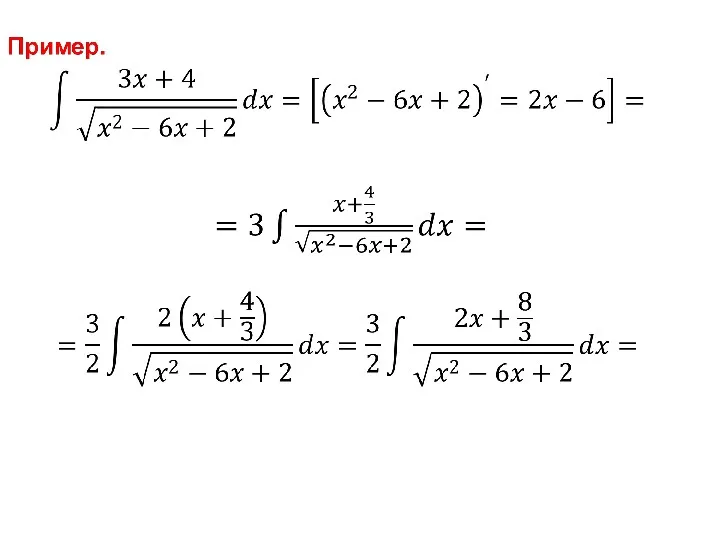

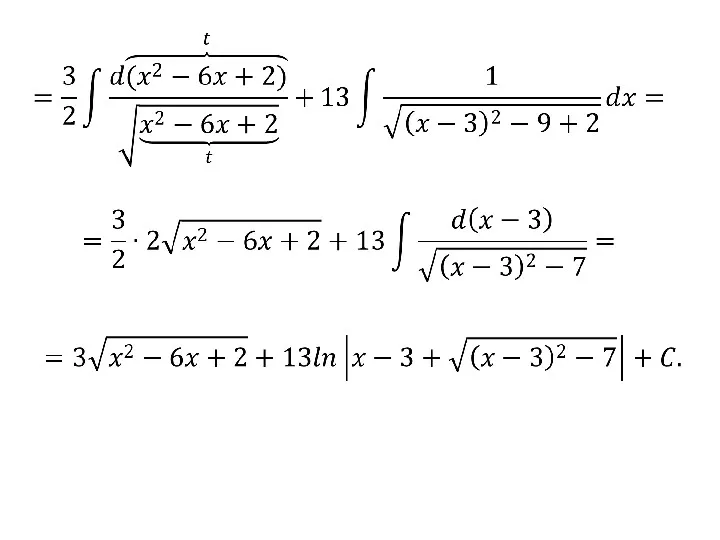

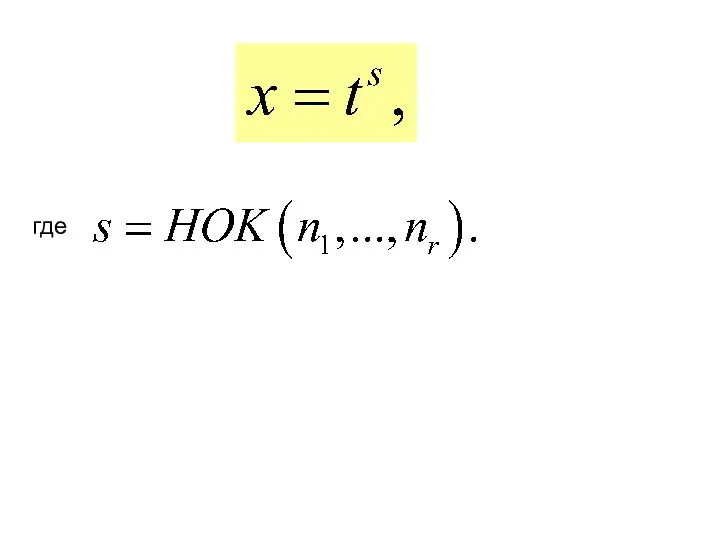
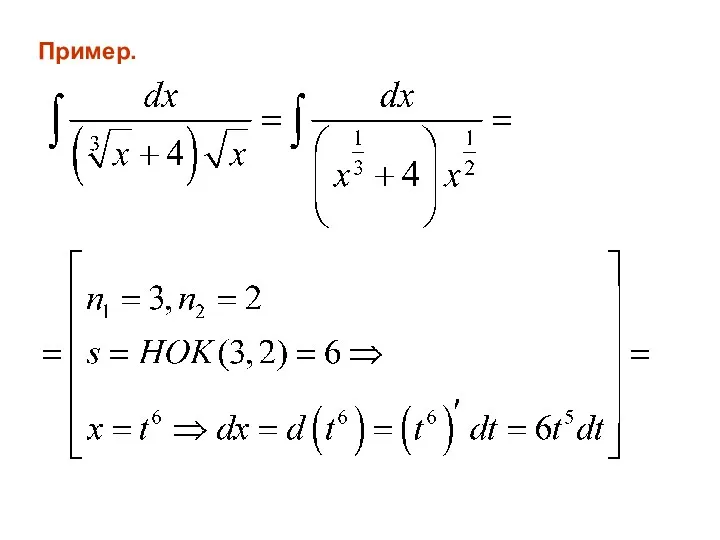
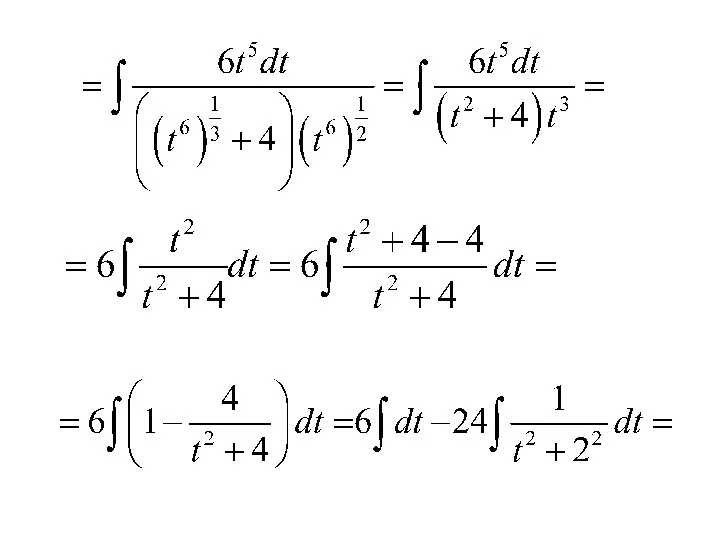
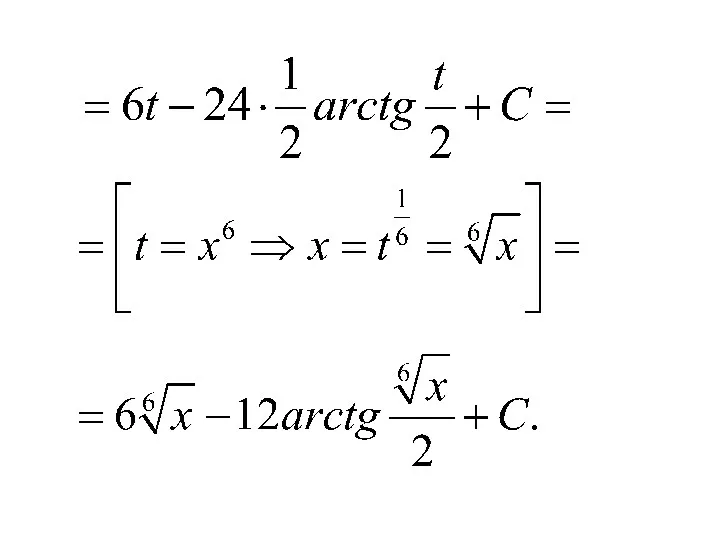

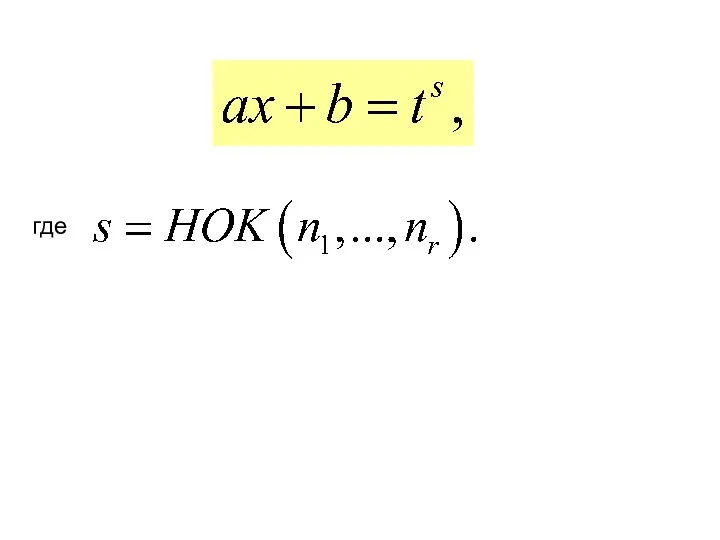
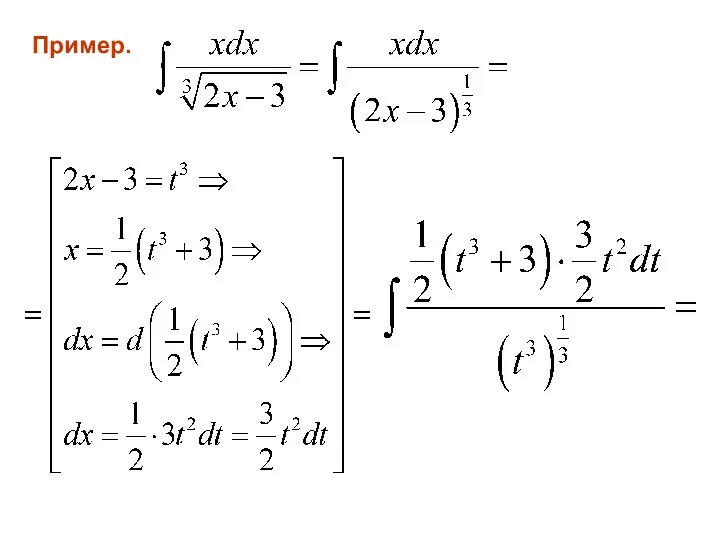
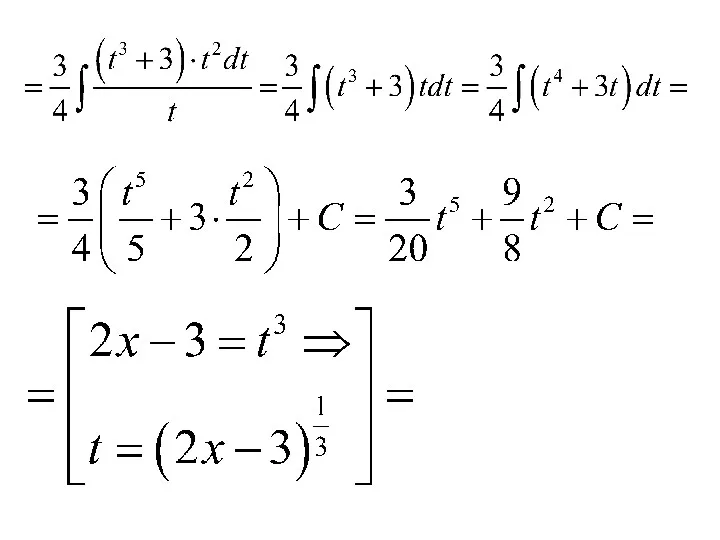
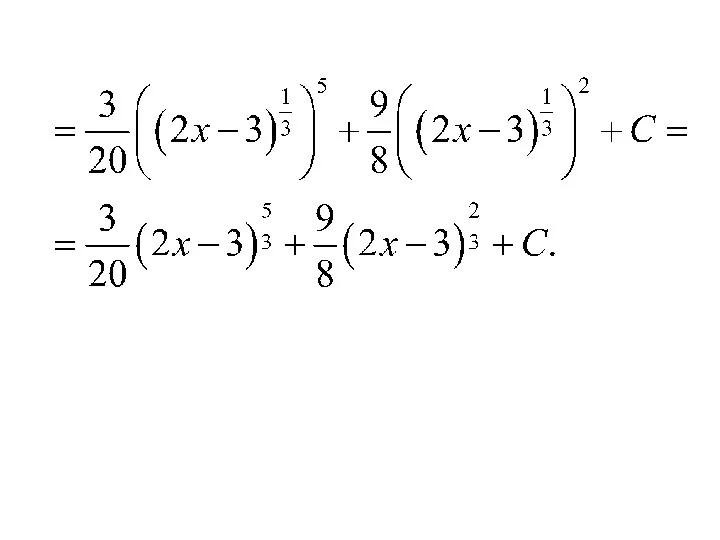

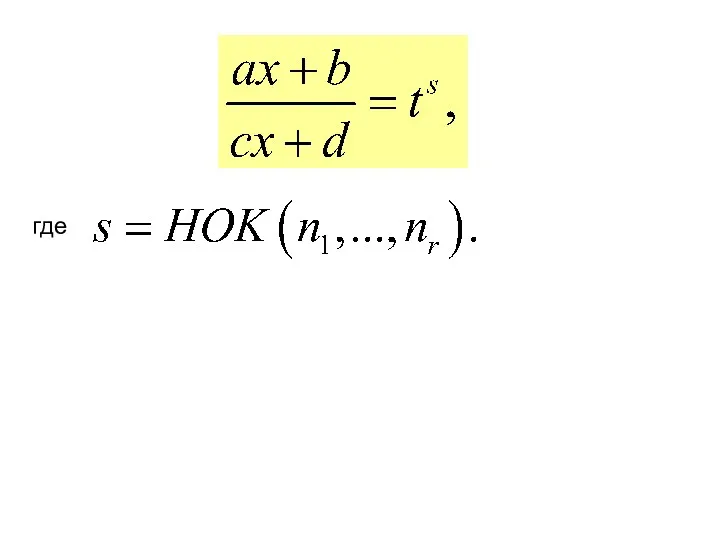













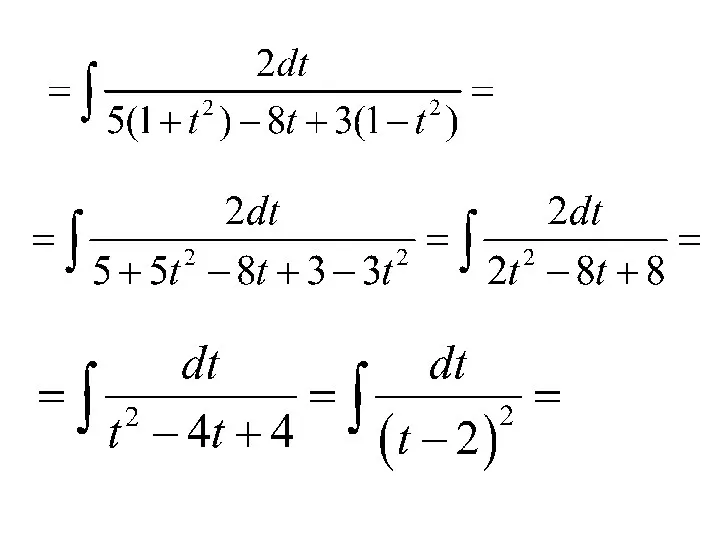



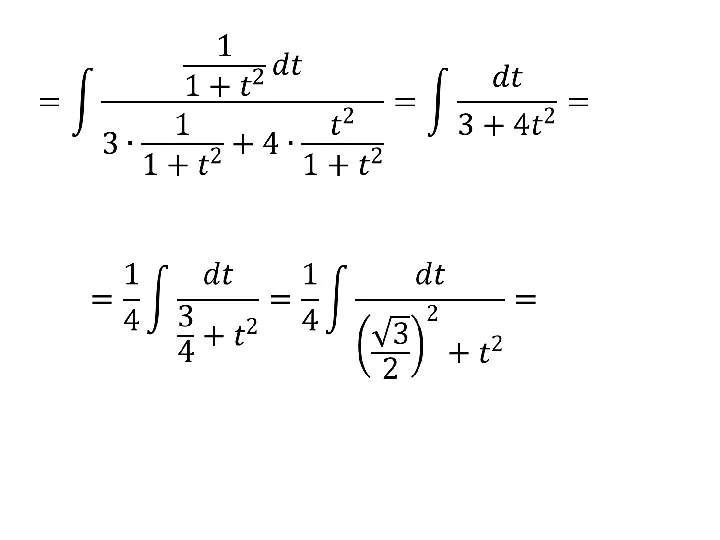
 Преобразование выражений с радикалами
Преобразование выражений с радикалами Возрастание и убывание функции
Возрастание и убывание функции Сумма углов треугольника. Внешний угол треугольника
Сумма углов треугольника. Внешний угол треугольника Сравнение величин углов. Классификация углов по градусной мере
Сравнение величин углов. Классификация углов по градусной мере Правильные многогранники в архитектуре
Правильные многогранники в архитектуре Интеллектуальная игра: Морской бой
Интеллектуальная игра: Морской бой Презентация +8, +9 с переходом через десяток
Презентация +8, +9 с переходом через десяток Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Развитие вычислительных навыков сложения и вычитания в пределах100.
Развитие вычислительных навыков сложения и вычитания в пределах100. Жай бөлшектерді бөлуді қайталау
Жай бөлшектерді бөлуді қайталау Устная работа к урокам. Умножение обыкновенных дробей 6 класс 1-3 часть
Устная работа к урокам. Умножение обыкновенных дробей 6 класс 1-3 часть Линейная функция, её свойства и график
Линейная функция, её свойства и график Кусочно-заданные функции. 9 класс
Кусочно-заданные функции. 9 класс Слагаемые, сумма
Слагаемые, сумма Устный счёт 4 класс
Устный счёт 4 класс Сравнение дробей
Сравнение дробей Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Закрепление сложения и вычитания 1,2 Тема: Закрепление сложения и вычитания 1,2 Цели: Закрепить знания случаев сложения и вычитания вида □±1,□±2,умение составлять и решать прямые и обратные задачи; закрепить знания состава
Закрепление сложения и вычитания 1,2 Тема: Закрепление сложения и вычитания 1,2 Цели: Закрепить знания случаев сложения и вычитания вида □±1,□±2,умение составлять и решать прямые и обратные задачи; закрепить знания состава Упрощение выражений
Упрощение выражений Построение треугольника по основанию, углу при вершине и высоте
Построение треугольника по основанию, углу при вершине и высоте Теорема Пифагора
Теорема Пифагора Раньше, позже, сначала, потом
Раньше, позже, сначала, потом Приёмы устных вычислений вида 450+30, 620-200
Приёмы устных вычислений вида 450+30, 620-200 Смешанные числа. Задачи
Смешанные числа. Задачи Квадрат суммы двух чисел
Квадрат суммы двух чисел Приемы устных вычислений. 3 класс
Приемы устных вычислений. 3 класс Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Сравнение дробей
Сравнение дробей