Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле презентация
Содержание
- 2. Математика ППИ Лекция 11. Неопределённый интеграл . Методы интегрирования: замена переменной.
- 3. Цели и задачи: Дать понятие первообразной и неопределенного интеграла. Изучить основные свойства интеграла.
- 4. Цели и задачи: Изучить основные методы интегрирования: интегрирование методом замены переменной, по частям.
- 5. Вопросы лекции 1. Первообразная и неопределенный интеграл. 2. Основные свойства неопределённого интегра. 3.Интегрирование разложением, внесением под
- 6. ЛИТЕРАТУРА [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004. с. 340-375; [3]
- 7. Интеграл (от лат. integer — целый), одно из важнейших понятий математики. Оно возникло в связи с
- 8. А с другой — измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и
- 9. Немецкий учёный Г. Лейбниц одновременно с английским учёным И. Ньютоном и независимо от него открыл основные
- 10. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование –
- 11. Лейбниц Готфрид Вильгельм (1646-1716) Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы
- 12. Огюстен Луи Коши (1789 – 1857) Карл Теодор Вильгельм Вейерштрасс (1815 -1897 ) Работы Коши и
- 13. Огюстен Луи Коши (1789 – 1857) Карл Теодор Вильгельм Вейерштрасс (1815 -1897 ) Работы Коши и
- 14. Учебный вопрос. Первообразная и неопределенный интеграл.
- 15. Первообразная и неопределённый интеграл. Определение. Функция F(x) называется первообразной для функции f(x) на отрезке [a; b]
- 16. Замечание. Задача отыскания функции по заданной производной этой функции решается, например, в инерциальных системах счисления пути
- 17. Пример. Рассмотрим функцию и найдём её первообразные. Решение. Первообразные
- 18. Теорема. Если F(x) – первообразная для функции f(x), то любая первообразная для f(x) имеет вид Ф(x)=F(x)+C,
- 19. Доказательство. В силу определения первообразной : F’(x)=f(x). Пусть Ф(x) – другая первообразная, тогда Ф’(x)=f(x). Рассмотрим функцию
- 20. Определение. Совокупность всех первообразных для функции f(x) на некотором интервале называется неопределённым интегралом от функции f(x)
- 21. Пример. Проверим результат: Отыскание всех первообразных для данной функции или одной из них называется интегрированием. Интегрирование
- 22. Естественно возникает вопрос: для всякой ли функции существуют первообразные, а значит и неопределённый интеграл? На этот
- 23. УЧЕБНЫЙ ВОПРОС, Основные свойства неопределённого интеграла.
- 24. Основные свойства неопределённого интеграла. 1. Производная от неопределённого интеграла равна подынтегральной функции: если , то 2.
- 25. 3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции, плюс произвольная постоянная Справедливость последующего равенства
- 26. 4. Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых
- 27. 5. Числовой множитель можно выносить за знак неопределенного интеграла: .
- 28. 6. Свойство инвариантности (постоянства) формул интегрирования. Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой
- 29. Доказательство. Возьмём функцию для её дифференциала в силу теоремы об инвариантности вида первого дифференциала имеем: отсюда
- 30. 7.
- 31. 1.f(x) = хn 2.f(x) = C 3.f(x)=sinx 4.f(x) = 6.f(x)= а. F(x) =Сх+С1 б. F(x) =
- 32. Таблица основных интегралов (через u(x)!) 1. 2. 3. 4. 5.
- 33. 6. 7. 8. 9. 10.
- 34. 11. 12. 13. 14.
- 35. 15. 16.
- 36. Замечание. Таблица основных интегралов в силу свойства инвариантности формул интегрирования оказывается справедливой независимо от того, является
- 37. Пример.
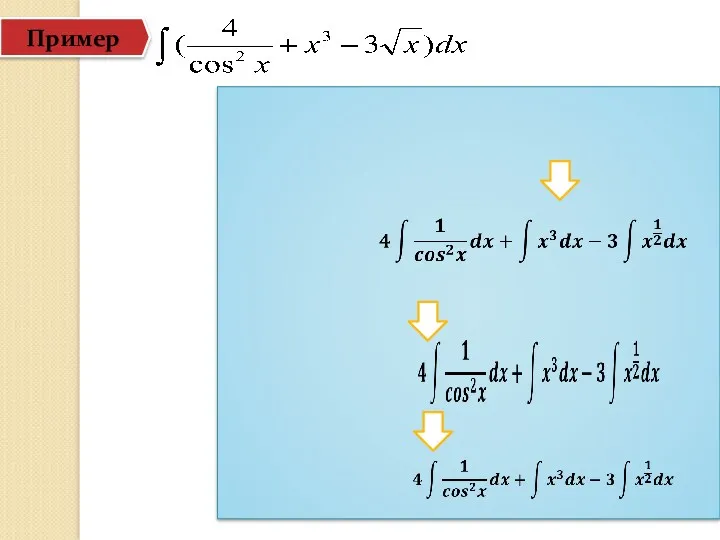
- 38. Пример
- 39. Найти интегралы для функций: F(x) = 5 х² + C F(x) = х³ + C F(x)
- 40. Верно ли что: а) в) б) г)
- 41. УЧЕБНЫЙ ВОПРОС Интегрирование разложением, внесением под знак дифференциала.
- 42. Непосредственное интегрирование - вычисление интеграла с помощью его свойств, тождественных преобразований подынтегральной функции, таблицы основных интегралов.
- 43. Таблица основных интегралов в силу свойства инвариантности формул интегрирования оказывается справедливой независимо от того, является ли
- 44. Найти интеграл Решение:
- 45. Интегрирование внесением под знак дифференциала. Известно, что дифференциал функции равен произведению производной этой функции и дифференциала
- 46. Таблица дифференциалов
- 47. Пусть требуется найти интеграл вида Подводя в этом интеграле множитель под знак дифференциала, а затем используя
- 48. Метод интегрирования введением под знак дифференциала используется для интегрирования сложных функций: аргумент сложной функции записывается под
- 49. Пример. Найти интеграл Здесь подынтегральное выражение разделено на 2, так как
- 50. Теперь используем свойство инвариантности и применим формулу 1 таблицы относительно переменной интегрирования 2х – 3. Таким
- 51. Примеры.
- 52. 1.f(x) = хn 2.f(x) = C 3.f(x)=sinx 4.f(x) = 6.f(x)= 1. F(x) =Сх+С1 2. F(x) =
- 53. УЧЕБНЫЙ ВОПРОС Метод замены переменной в неопределенном интеграле. Интегрирование функций, содержащих квадратный трехчлен.
- 54. Замена переменной или подстановка. Метод заключается во введении новой переменной интегрирования. При этом интеграл приводится к
- 55. Введём в интеграле новую переменную t, положив x=φ(t), где φ(t) – непрерывная, дифференцируемая функция. Тогда dx=φ’(t)
- 56. Доказательство. Находим производную от левой части равенства . Правую часть равенства будем дифференцировать по x как
- 57. Таким образом, имеем Следовательно, производные по х от правой и левой частей равенства равны, что и
- 58. Замечание 1. После интегрирования в правой части равенства вместо t необходимо подставить его выражение через x
- 61. Интегрирование функций, содержащих квадратный трехчлен.
- 64. Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004,
- 65. Математика ППИ Лекция 12. Метод интегрирования по частям в неопределенном интеграле. Интегрирование тригонометрических функций
- 66. Вопросы лекции 1. Интегрирование по частям в неопределенном интеграле. 2. Интегрирование тригонометрических функций.
- 67. УЧЕБНЫЙ ВОПРОС Интегрирование по частям.
- 68. Одной из причин сложности операции интегрирования является отсутствие формулы интегрирования произведения функций. Есть метод интегрирования произведения
- 69. Пусть u=u(x) и v=v(x) – дифференцируемые функции и Отсюда, интегрируя последнее равенство, получаем: или формулой интегрирования
- 70. Успех формулы интегрирования по частям зависит от умения правильно разбить подынтегральное выражение на множители u и
- 71. I. Интегралы вида: где P(x) – многочлен. Во всех случаях за u при интегрировании по частям
- 73. Решение. (опечатка в du) v
- 76. Скачать презентацию




![ЛИТЕРАТУРА [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/218812/slide-5.jpg)




















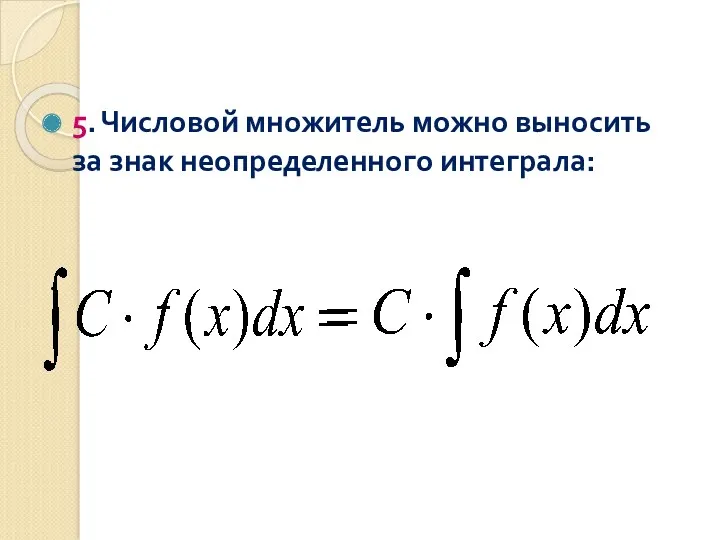


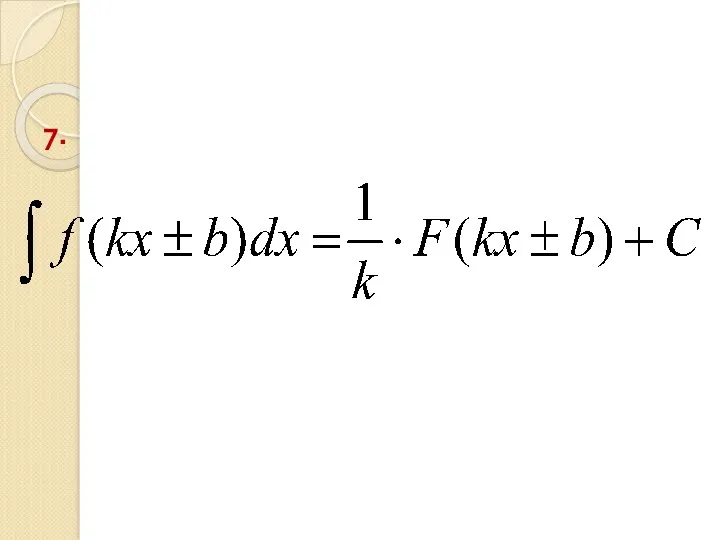


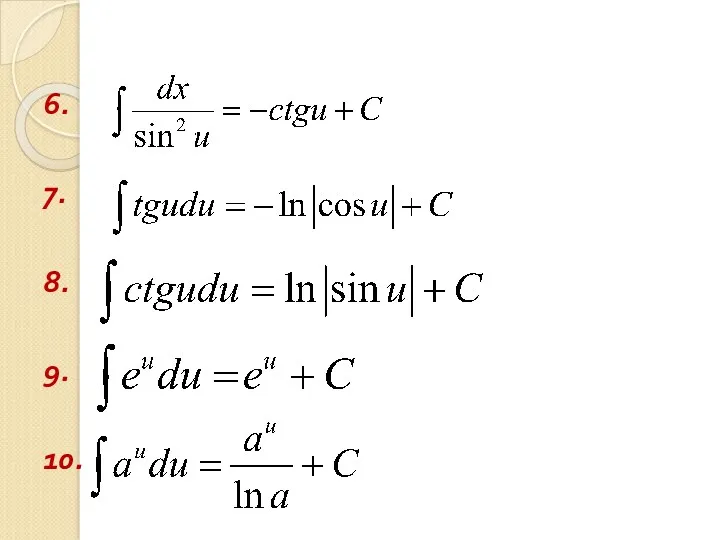
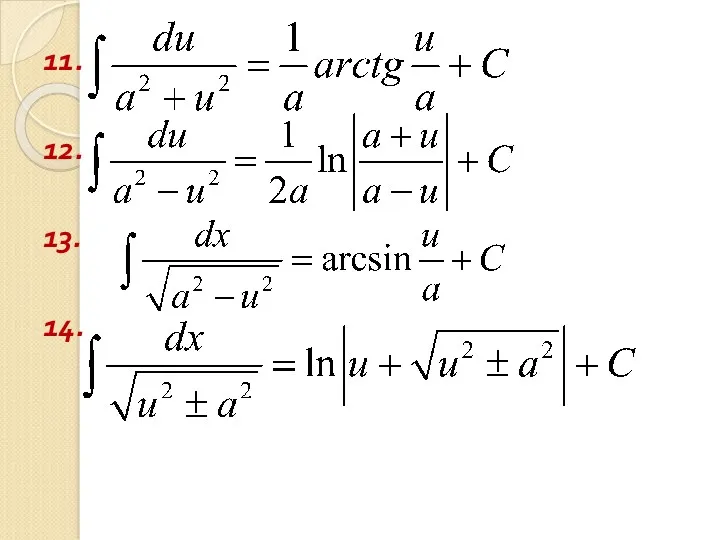
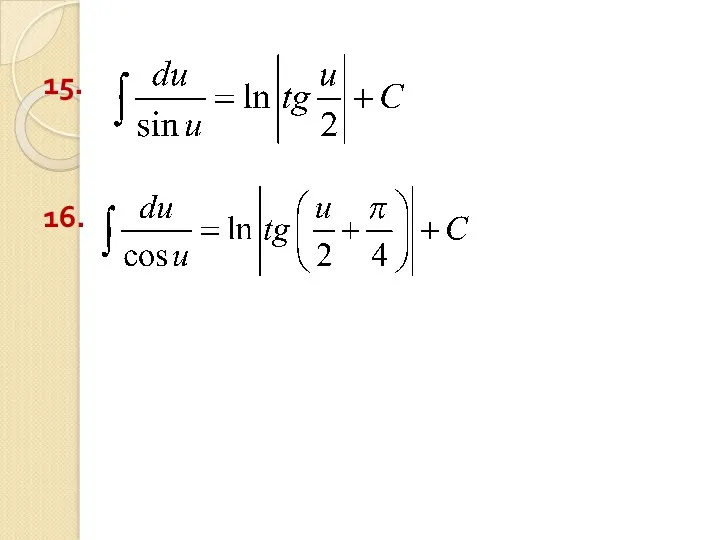

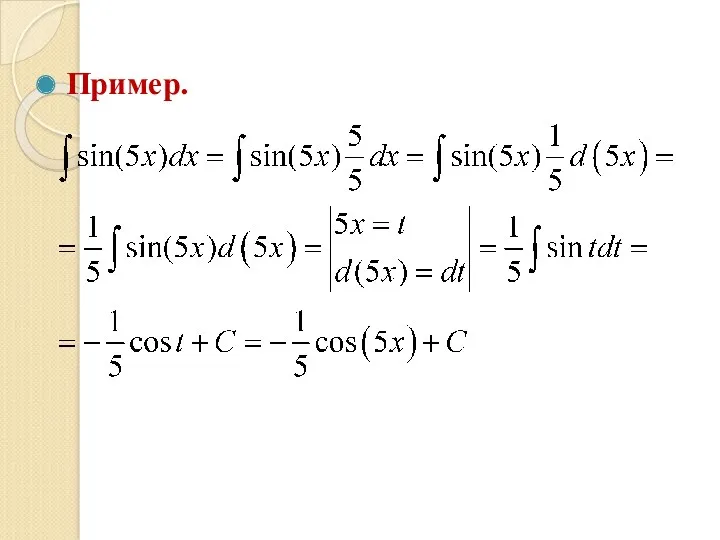




















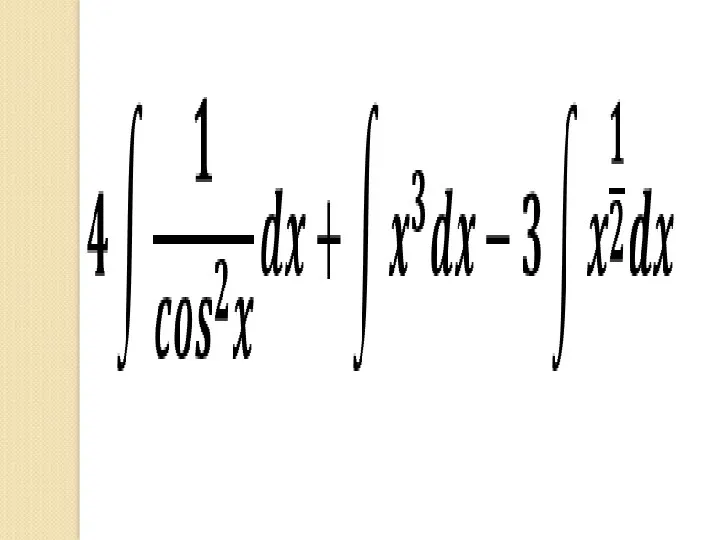
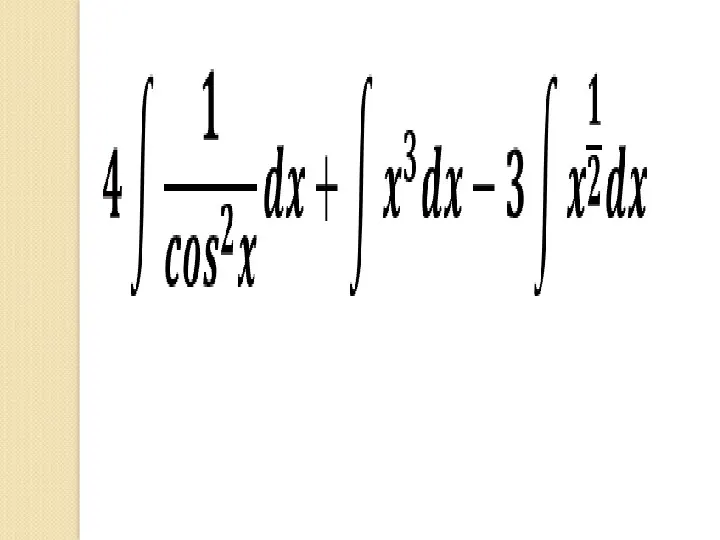



![Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/218812/slide-63.jpg)







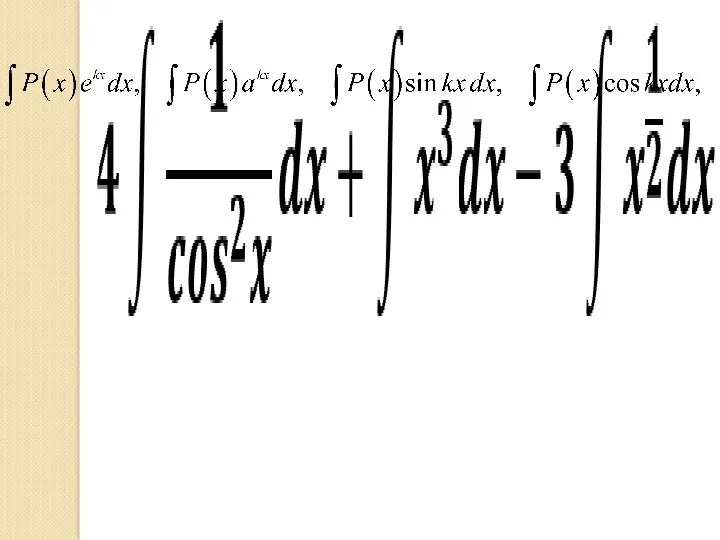

 Начертательная геометрия. Пересечение поверхности плоскостью общего положения. (Лекция 7)
Начертательная геометрия. Пересечение поверхности плоскостью общего положения. (Лекция 7) Omówienie sprawdzianu
Omówienie sprawdzianu Уравнение множественной регрессии
Уравнение множественной регрессии Алгебра логики. Контрольная работа
Алгебра логики. Контрольная работа Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств
Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств Готовимся к ГИА
Готовимся к ГИА Плоскость. Уравнения плоскости
Плоскость. Уравнения плоскости Геометрический турнир
Геометрический турнир Треугольник и его виды
Треугольник и его виды Тесты для интерактивной доски по УМК Школа России
Тесты для интерактивной доски по УМК Школа России Математика вокруг нас. Конкурс смекалки
Математика вокруг нас. Конкурс смекалки Центральные и вписанные углы
Центральные и вписанные углы Нахождение числа по его дроби
Нахождение числа по его дроби Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения)
Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения) Уравнение окружности. Урок геометрии в 9 классе
Уравнение окружности. Урок геометрии в 9 классе Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3)
Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3) Формирование УУД на уроках математики
Формирование УУД на уроках математики Статистическая обработка данных. Повторение
Статистическая обработка данных. Повторение Методы и модели линейного программирования. Лекция 4
Методы и модели линейного программирования. Лекция 4 Чисельні методи (ЧМ)
Чисельні методи (ЧМ) Делимость натуральных чисел
Делимость натуральных чисел Определение показательной функции
Определение показательной функции Презентация к уроку математики 2 кл
Презентация к уроку математики 2 кл Симметрия в природе
Симметрия в природе Формулы приведения, формулы сложения. Формулы удвоения. Формулы половинного угла
Формулы приведения, формулы сложения. Формулы удвоения. Формулы половинного угла Информатика в задачах теплоэнергетики
Информатика в задачах теплоэнергетики Презентация к уроку математики Решение задач с помощью уравнения
Презентация к уроку математики Решение задач с помощью уравнения Медиа-сопровождение к уроку математики Число 9. Цифра 9
Медиа-сопровождение к уроку математики Число 9. Цифра 9