Содержание
- 2. Непрерывная случайная величина (НСВ) может принимать все значения из некоторого конечного или бесконечного промежутка Функция распределения
- 3. Свойства функции распределения
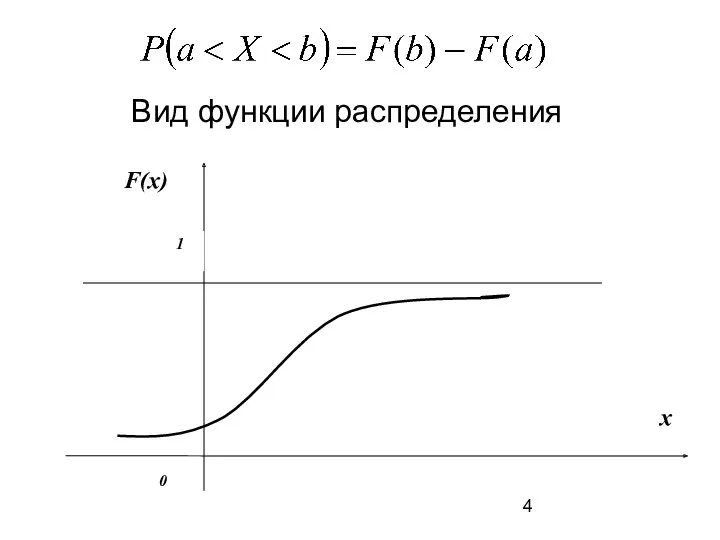
- 4. Вид функции распределения
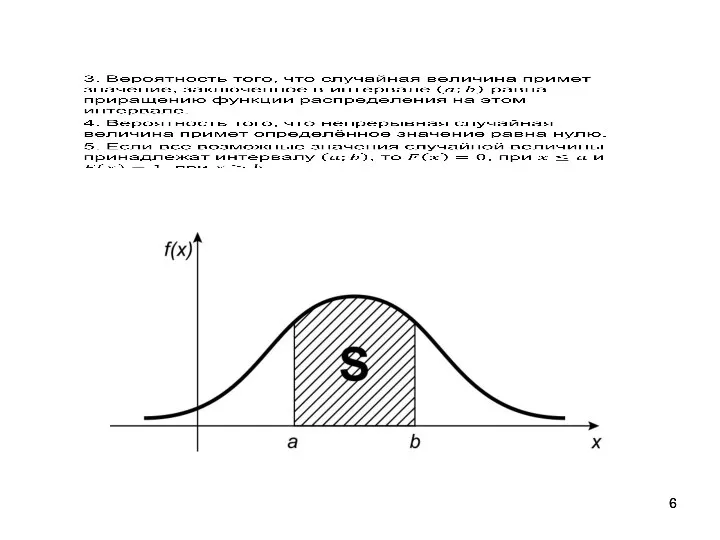
- 5. Функция плотности распределения вероятностей
- 7. Свойства функции плотности
- 8. Математическое ожидание
- 9. Дисперсия
- 10. Равномерное распределение НСВ задается равномерным законом распределения, если на интервале, которому принадлежат все ее возможные значения,
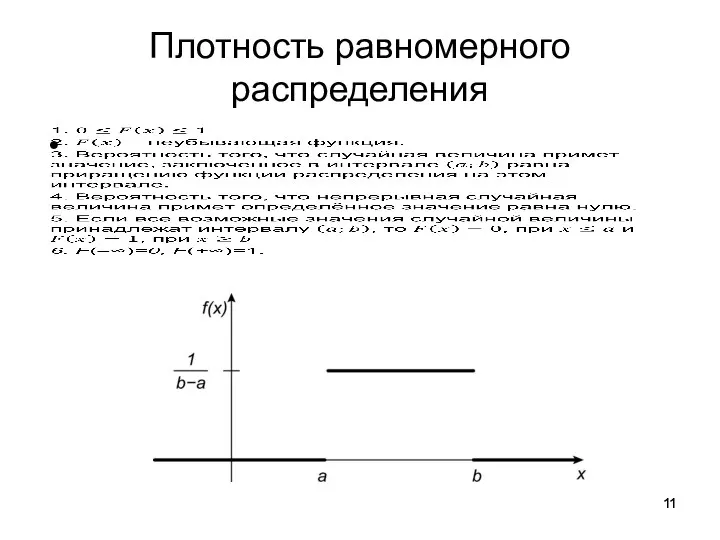
- 11. Плотность равномерного распределения
- 12. Функция распределения равномерного распределения Числовые характеристики равномерного распределения
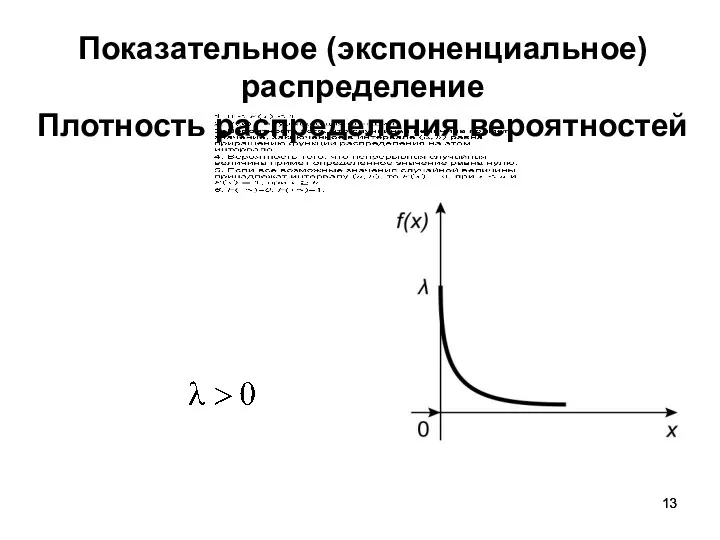
- 13. Показательное (экспоненциальное) распределение Плотность распределения вероятностей
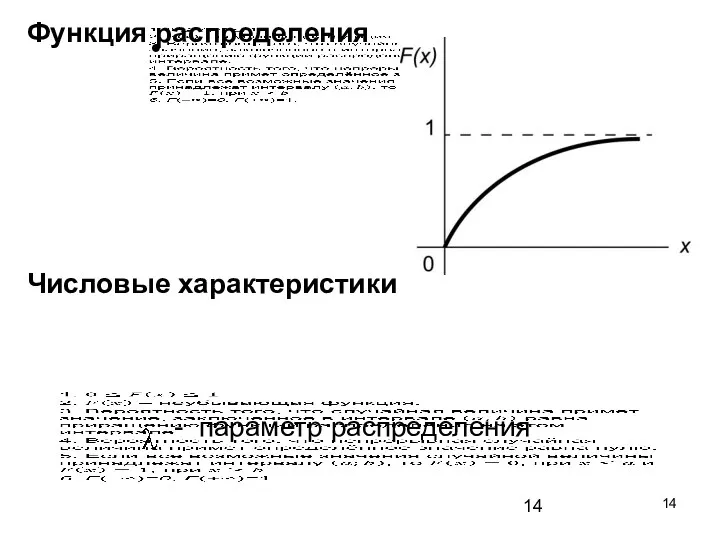
- 14. Функция распределения Числовые характеристики - параметр распределения
- 15. Применение показательного распределения. Функция надежности Время T между появлениями двух последовательных событий простейшего потока случайных событий
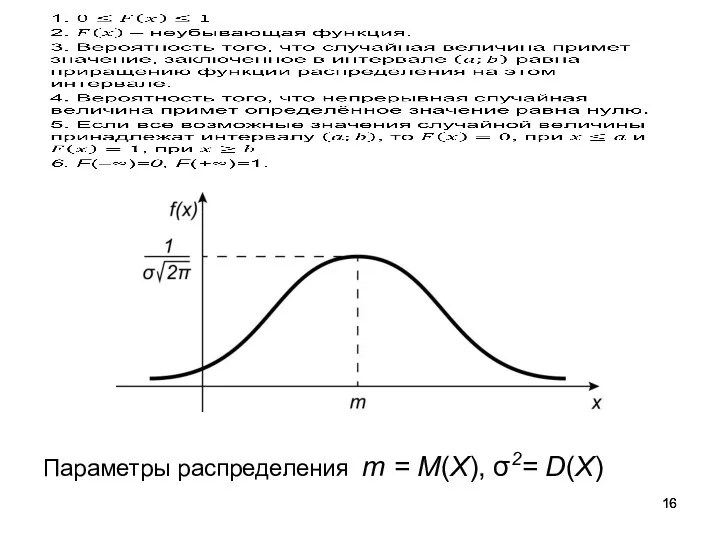
- 16. Параметры распределения m = M(X), σ2= D(X)
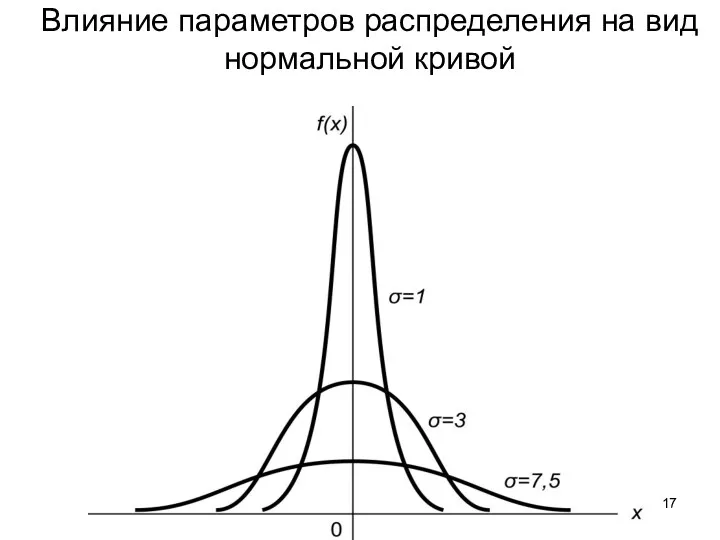
- 17. Влияние параметров распределения на вид нормальной кривой
- 18. Вероятность попадания в интервал Функция распределения
- 19. Правило трёх сигм Вероятность отклонения по абсолютной величине от среднего
- 20. Центральная предельная теорема Ляпунова (ЦПТ) Теорема утверждает, что если случайная величина образуется в результате сложения большого
- 21. Одна из формулировок ЦПТ Пусть СВ Х имеет конечное М(Х) и D(Х), тогда распределение среднего арифметического
- 22. Распределения, связанные с нормальным Распределение «хи-квадрат» Пусть Хi (i=1,2,…,n) нормированные, M(Хi)=0 D(Хi)=1, нормально распределенные СВ, тогда
- 23. Плотность распределения «хи-квадрат» Где - гамма- функция
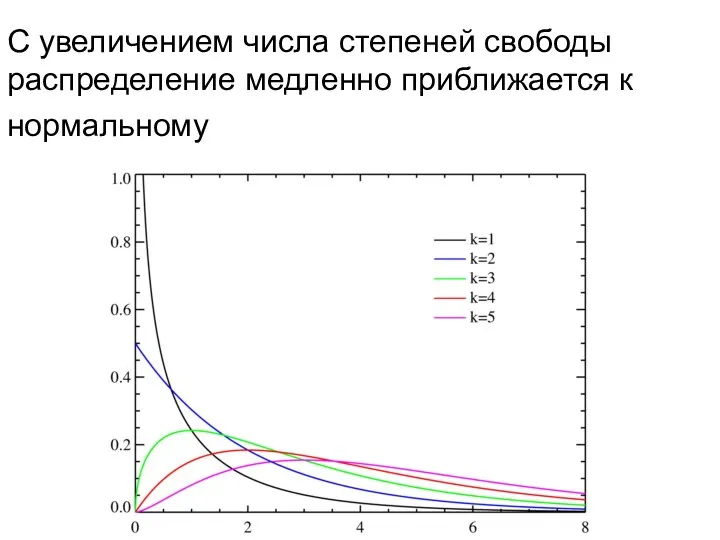
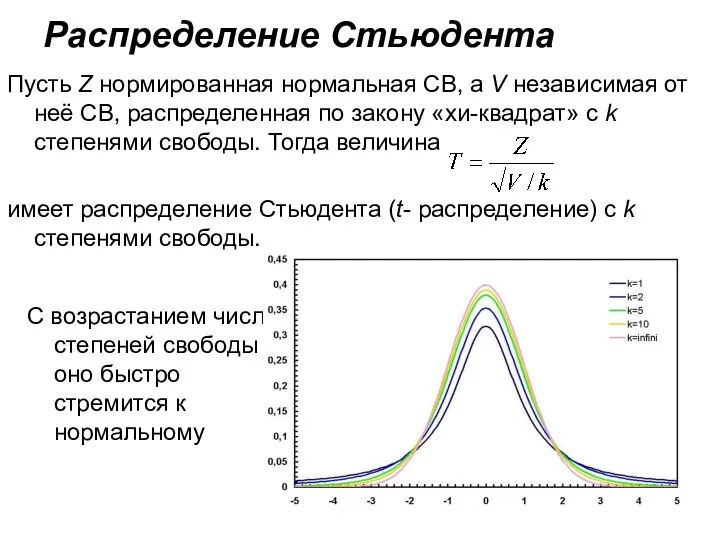
- 24. С увеличением числа степеней свободы распределение медленно приближается к нормальному
- 25. Распределение Стьюдента Пусть Z нормированная нормальная СВ, а V независимая от неё СВ, распределенная по закону
- 26. Контрольные вопросы по теме лекции 1. Непрерывная случайная величина. Функция распределения и ее свойства. 2. Плотность
- 28. Скачать презентацию
















 История возникновения нуля, его значение в жизни человека
История возникновения нуля, его значение в жизни человека Зручний спосіб обчислення. Віднімання двоцифрових чисел. Задача на різницеве порівняння. Урок №127
Зручний спосіб обчислення. Віднімання двоцифрових чисел. Задача на різницеве порівняння. Урок №127 Выборочное наблюдение
Выборочное наблюдение Математический квест
Математический квест Математические законы в творчестве Пушкина
Математические законы в творчестве Пушкина Сфера и шар
Сфера и шар Презентация Открытые задачи
Презентация Открытые задачи Формирование вычислительной культуры обучающихся основной школы
Формирование вычислительной культуры обучающихся основной школы Умножение и деление натуральных чисел и их свойства. 5 класс
Умножение и деление натуральных чисел и их свойства. 5 класс Теорема Пифагора
Теорема Пифагора Математичні хвилинки
Математичні хвилинки Презентация к уроку математики на тему Арифметические действия над числами
Презентация к уроку математики на тему Арифметические действия над числами Случайные события. Вероятность случайного события
Случайные события. Вероятность случайного события Сумма углов треугольника. Тренировочные упражнения
Сумма углов треугольника. Тренировочные упражнения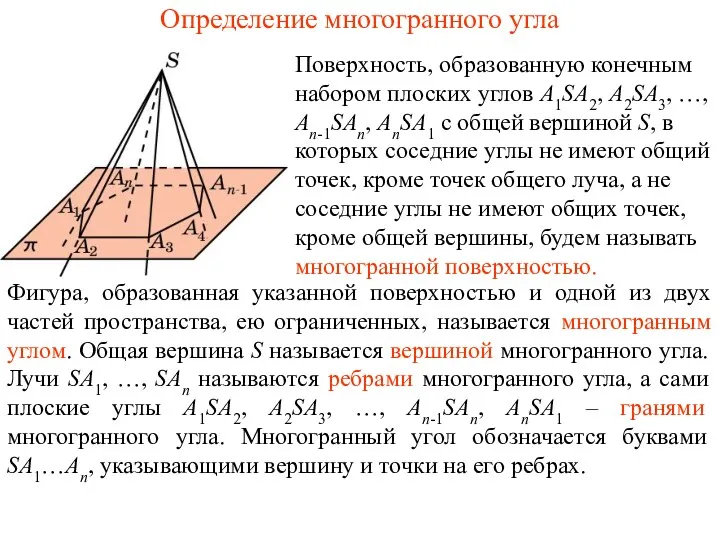 Определение многогранного угла
Определение многогранного угла Решение текстовых задач при подготовке к ГИА
Решение текстовых задач при подготовке к ГИА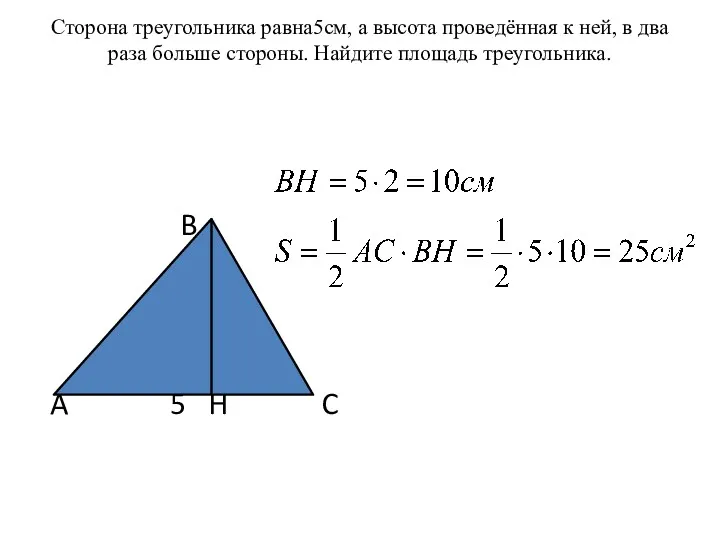 Решение задач. Площадь треугольника
Решение задач. Площадь треугольника Смежные и вертикальные углы
Смежные и вертикальные углы Види трикутників
Види трикутників Цилиндр. Площадь его поверхности
Цилиндр. Площадь его поверхности Квадрат и куб числа
Квадрат и куб числа Метод множителей Лагранжа
Метод множителей Лагранжа Аттракторы динамических систем
Аттракторы динамических систем Число 4. Цифра4.
Число 4. Цифра4. Площадь многоугольников. Теорема Пифагора. Решение задач
Площадь многоугольников. Теорема Пифагора. Решение задач Признаки параллельности прямых
Признаки параллельности прямых Алгебраические дроби. Сокращение алгебраических дробей
Алгебраические дроби. Сокращение алгебраических дробей Подготовка к ОГЭ. Модуль геометрия
Подготовка к ОГЭ. Модуль геометрия