Слайд 2

определена
Пример : в точке x = 0 не определена , но
Предел
Слайд 3

Бесконечно малые, бесконечно большие функции Неопределенности
.
Повтор лекции 2
Повтор лекции 2
Слайд 4

.
Два замечательных предела
Рассмотренные свойства функций, имеющих предел в точке
a ∈ ℜ расширенной числовой прямой, дают возможность проанализировать их поведение в окрестности этой точки a . Однако в ряде случаев этих свойств и установленных правил предельного перехода недостаточно. Одним из классических примеров подобного случая является поведение функции
(sin x) / x в окрестности точки a = 0 .
Пусть х - центральный угол окружности единичного радиуса , причем 0 < x < π/2 (см. следующий слайд).
Слайд 5
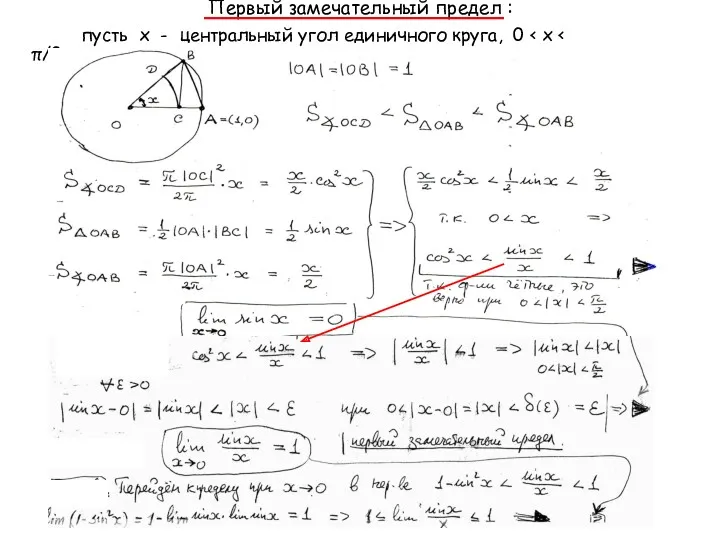
Первый замечательный предел :
пусть х - центральный угол единичного
круга, 0 < x < π/2.
Слайд 6

.
При этом , т.е. последовательность
возрастает и она ограничена :
Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Определение Пусть f(x) и g(x) определены в Ú(a) .
Если ,
то функции f(x) и g(x) называются эквивалентными (асимптотически равными) при х → a . Обозначение: f ~ g , х → a .
Пример : sin x ~ x , х → 0 .
Теорема (критерий эквивалентности функций)
Слайд 12

Слайд 13

Слайд 14

Слайд 15
Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

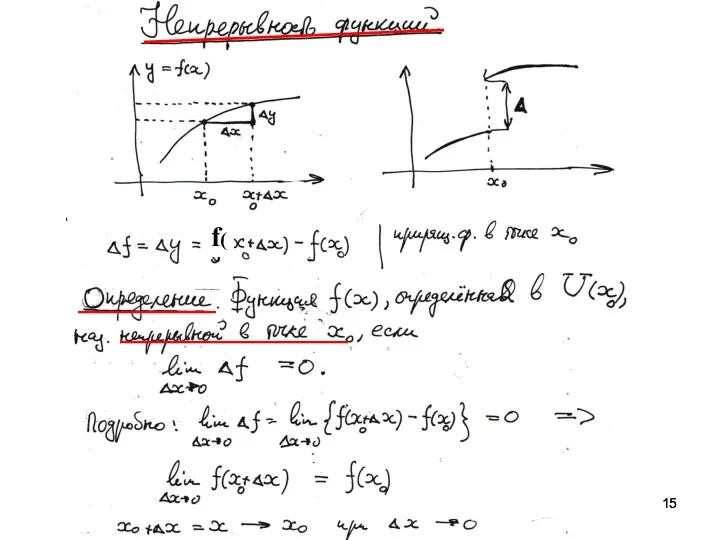
Свойства функций, непрерывных в точке
Если функция f(x) непрерывна в
точке α ∈ ℜ , то она имеет конечный предел в ней, ограничена в окрестности т. α и при условии f(x) ≠ 0 знакопостоянна. Из правил предельного перехода при арифметических операциях следуют свойства непрерывности:
Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

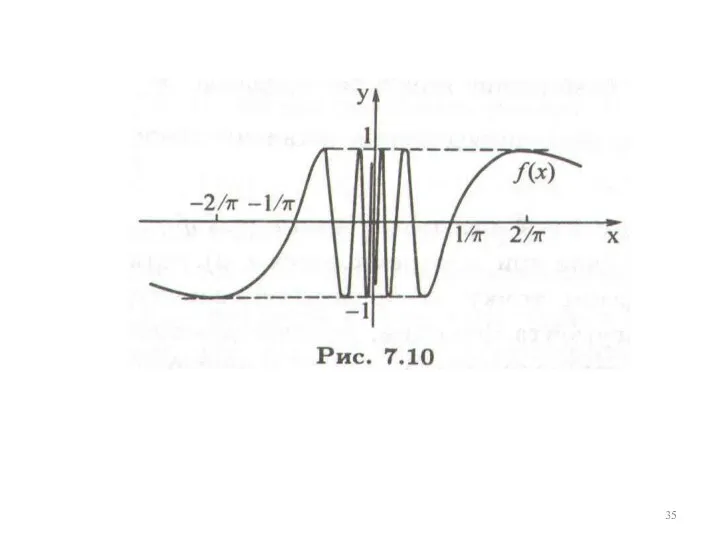
Точка разрыва первого рода – существование обоих односторонних конечных пределов
≡≡≡≡
≡≡≡≡
Рис. 9.4
Слайд 32

Слайд 33

Точка разрыва первого рода – существование обоих односторонних . конечных пределов
.
Слайд 34

Слайд 35
Слайд 36

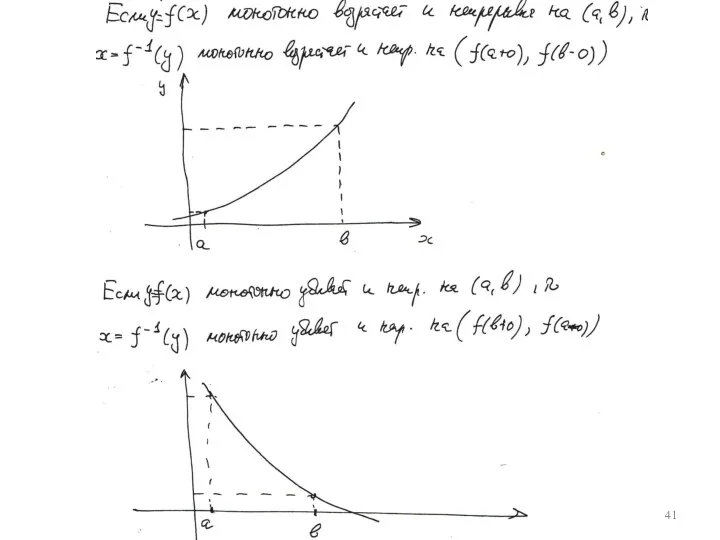
Свойства непрерывных функций
Рис. 9.6
Слайд 37

Теорема о промежуточном значении непрерывной функции
Слайд 38

Слайд 39

Слайд 40

Слайд 41
Слайд 42

Слайд 43

Слайд 44












































 Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их числовые характеристики
Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их числовые характеристики Арифметическая прогрессия
Арифметическая прогрессия Уроки математики по теме Точка. Прямая линия. Кривая линия. Отрезок. Луч. Ломаная линия (3 часа), 1 класс, УМК Гармония
Уроки математики по теме Точка. Прямая линия. Кривая линия. Отрезок. Луч. Ломаная линия (3 часа), 1 класс, УМК Гармония МароваСН конкурс презент подготовка ОГЭ
МароваСН конкурс презент подготовка ОГЭ Анализ результатов выполнения экзаменационной работы по математике в 2019 году
Анализ результатов выполнения экзаменационной работы по математике в 2019 году Обыкновенные дроби
Обыкновенные дроби Решение метрологических задач
Решение метрологических задач Методика подготовки учащихся к решению задач раздела Реальная математика (ОГЭ и ЕГЭ)
Методика подготовки учащихся к решению задач раздела Реальная математика (ОГЭ и ЕГЭ) Круг. Площадь круга
Круг. Площадь круга Основы комбинаторного анализа. Формулы простого перечисления. (Лекции 16-18)
Основы комбинаторного анализа. Формулы простого перечисления. (Лекции 16-18)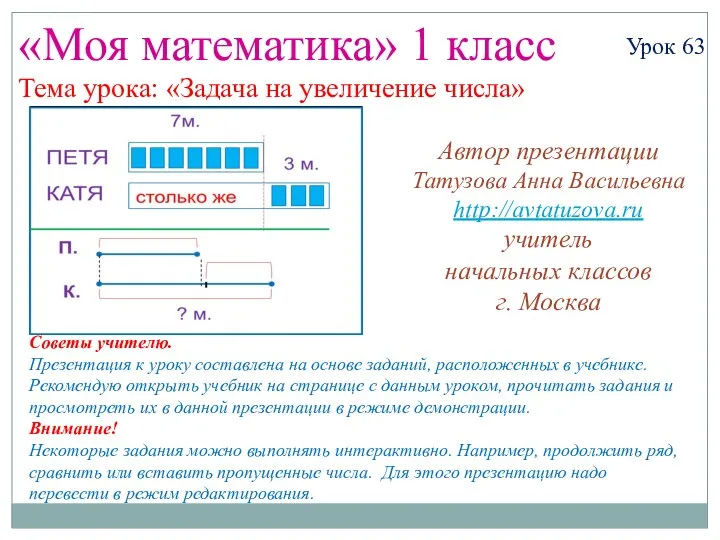 Математика. 1 класс. Урок 63. Задача на увеличение числа - Презентация
Математика. 1 класс. Урок 63. Задача на увеличение числа - Презентация Час ,минута. Определение времени по часам
Час ,минута. Определение времени по часам Математический диктант № 8. 2 класс
Математический диктант № 8. 2 класс Деление десятичных дробей
Деление десятичных дробей По дороге к Деду Морозу. Урок-сказка
По дороге к Деду Морозу. Урок-сказка Сопровождение исследовательской деятельности обучающихся как условие реализации ФГОС
Сопровождение исследовательской деятельности обучающихся как условие реализации ФГОС Сравнение дробей
Сравнение дробей Шкала. Координатный луч
Шкала. Координатный луч Четыре замечательные точки треугольника. 8 класс
Четыре замечательные точки треугольника. 8 класс Олимпиада национальной технологической инициативы. Технологии беспроводной связи. Информатика. Математика
Олимпиада национальной технологической инициативы. Технологии беспроводной связи. Информатика. Математика Урок-путешествие в страну отрицательных чисел для 6 класса
Урок-путешествие в страну отрицательных чисел для 6 класса Новое свойство квадратных уравнений
Новое свойство квадратных уравнений ОГЭ по математике. Задание 16
ОГЭ по математике. Задание 16 Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Образование чисел из одного десятка и нескольких единиц. 1 класс
Образование чисел из одного десятка и нескольких единиц. 1 класс Algorytmy ewolucyjne
Algorytmy ewolucyjne Задачи на проценты. Площадь фигуры
Задачи на проценты. Площадь фигуры Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса