Содержание
- 2. 1. Несобственные интегралы с бесконечными пределами интегрирования (1 рода) Пусть функция y=f(x) определена и интегрируема на
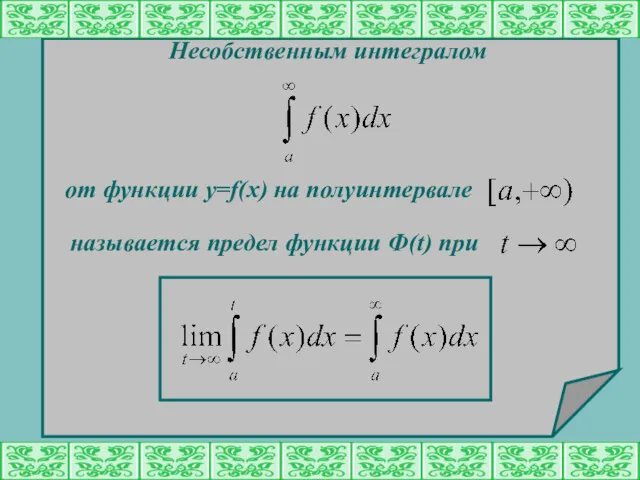
- 3. Несобственным интегралом от функции y=f(x) на полуинтервале называется предел функции Ф(t) при
- 4. Если такой предел существует и конечен, то несобственный интеграл называется сходящимся к данному пределу. Если конечного
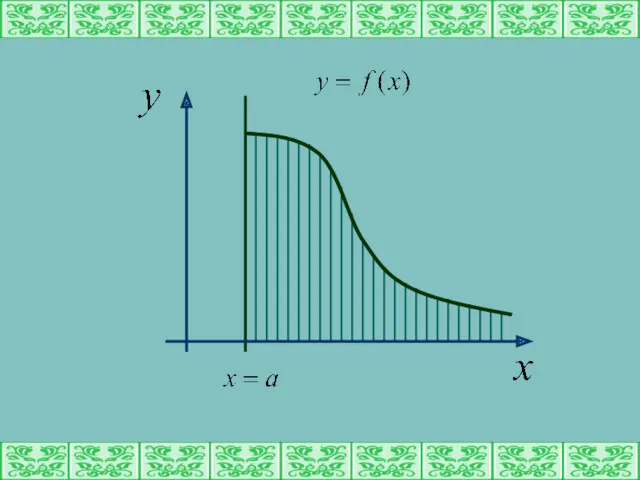
- 5. Геометрический смысл несобственного интеграла основан на геометрической интерпретации определенного интеграла на отрезке [a,t]. Это площадь бесконечной
- 7. Пример. Вычислить интеграл
- 8. Решение.
- 9. Аналогично можно определить несобственный интеграл на промежутке Рассмотрим несобственный интеграл на интервале Пусть для некоторого числа
- 10. - сходятся. Тогда положим и интеграл тоже сходится. Если хотя бы один из интегралов в левой
- 11. Пример. Вычислить интеграл
- 12. Решение. Исследуем на сходимость интегралы - сходится. - расходится. - расходится.
- 13. В рассмотренных примерах сначала с помощью первообразной вычислялся интеграл по конечному промежутку, а затем осуществлялся переход
- 14. Отсюда следует, что несобственный интеграл существует только в том случае, если существует конечный предел И тогда
- 15. Аналогично:
- 16. Пример. Вычислить интеграл
- 17. Решение.
- 18. 2. Несобственные интегралы от неограниченных функций (2 рода) Пусть функция y=f(x) непрерывна, но неограничена на полуинтервале
- 19. Несобственным интегралом от функции y=f(x) на полуинтервале называется предел где
- 20. Если такой предел существует и конечен, то несобственный интеграл называется сходящимся. Если конечного предела не существует,
- 21. Аналогично можно ввести понятие несобственного интеграла от функции y=f(x) непрерывной но неограниченой на полуинтервале (a,b]:
- 22. Пример. Вычислить интеграл
- 23. Решение. Особая точка х=0.
- 24. ЗАМЕЧАНИЕ 1. Если функция y=f(x) неограничена при х=С, где то интеграл тоже называется несобственным:
- 25. ЗАМЕЧАНИЕ 2. Если a и b – особые точки, т.е. функция y=f(x) неограничена и интегрируема на
- 26. Пример. Вычислить интеграл
- 27. Решение. Особые точки: х=-1, х=1.
- 28. Пусть функция y=f(x) интегрируема на всем промежутке [a,b], причем b – особая точка. Если существует первообразная
- 29. Пример. Вычислить интеграл
- 31. Скачать презентацию




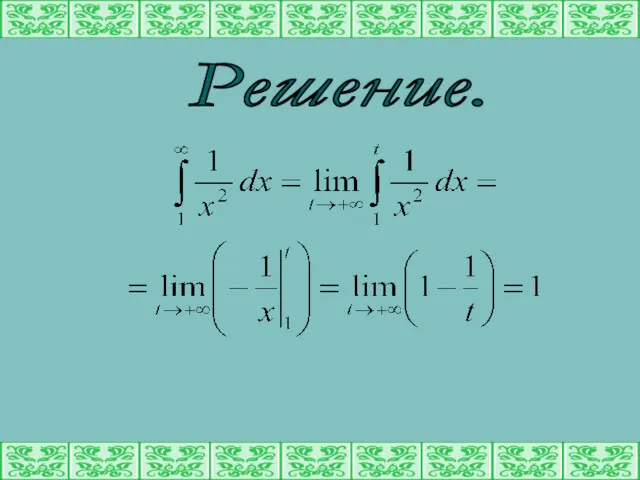












![Аналогично можно ввести понятие несобственного интеграла от функции y=f(x) непрерывной но неограниченой на полуинтервале (a,b]:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/132161/slide-20.jpg)






![Пусть функция y=f(x) интегрируема на всем промежутке [a,b], причем b](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/132161/slide-27.jpg)

 Презентация по математике Периметр и Площадь прямоугольника
Презентация по математике Периметр и Площадь прямоугольника Возникновение и развитие алгебры
Возникновение и развитие алгебры Освобождение от иррациональности в знаменателе дроби
Освобождение от иррациональности в знаменателе дроби Внешнее сопряжение двух окружностей
Внешнее сопряжение двух окружностей Самостоятельная работа учащихся на уроках математики
Самостоятельная работа учащихся на уроках математики методическая разработка Деление нацело и деление с остатком
методическая разработка Деление нацело и деление с остатком Формулы приведения. Тригонометрия-10 класс
Формулы приведения. Тригонометрия-10 класс математика +1,-1
математика +1,-1 Решение неравенств методом интервалов. 9 класс
Решение неравенств методом интервалов. 9 класс Математика. Дополни примеры цифрами Устный счет.
Математика. Дополни примеры цифрами Устный счет. Координатная плоскость
Координатная плоскость Основні поняття планіметрії
Основні поняття планіметрії Тіктөртбұрыш пен шаршының ауданы
Тіктөртбұрыш пен шаршының ауданы Движение вдогонку
Движение вдогонку Показательные уравнения и их системы
Показательные уравнения и их системы Уравнение окружности
Уравнение окружности Построение треугольников. Математика. 5 класс
Построение треугольников. Математика. 5 класс Способы решения уравнения sinX - cosX = 1
Способы решения уравнения sinX - cosX = 1 Трапеція. Середня лінія трапеції, трикутника
Трапеція. Середня лінія трапеції, трикутника Смешанные числа. Теоретический материал
Смешанные числа. Теоретический материал Коло, описане навколо трикутника. 7 клас
Коло, описане навколо трикутника. 7 клас Додавання і віднімання дробів з однаковими знаменниками
Додавання і віднімання дробів з однаковими знаменниками Двугранный угол
Двугранный угол Сравнение чисел
Сравнение чисел Умножение десятичных дробей
Умножение десятичных дробей Цікаві факти з історії геометрії
Цікаві факти з історії геометрії Расшифровка ребусов
Расшифровка ребусов Применение производной в различных областях естественных наук
Применение производной в различных областях естественных наук