Содержание
- 2. Из студенческого фольклора 27.11.2014 Студента после первой сессии спрашивают: - У вас в программе интегралы были?
- 3. Давайте вспомним! 1) неопределённый интеграл – это множество первообразных функций 2) определённый интеграл – это число
- 4. План 1. Несобственные интегралы I рода определение геометрическая интерпретация вычисление 2. Признаки сходимости несобственных интегралов I
- 5. задачи, приводящие к несобственным интегралам, рассматривались в геометрической форме Э. Торричелли и П. Ферма в 1644.
- 6. Точные определения Несобственных интегралов даны О. Коши в 1823. 27.11.2014
- 7. Несобственные интегралы I рода Определение 1: несобственным интегралом от функции в интервале называется предел интеграла при
- 8. Определение 2: несобственным интегралом от функции в интервале называется предел интеграла при , то есть Если
- 9. Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции
- 10. ЗАМЕЧАНИЕ Несобственный интеграл называют сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если
- 11. Несобственные интегралы (или интегралы Римана) I рода - это интегралы с бесконечными пределами интегрирования 27.11.2014
- 12. 27.11.2014 Вычисление несобственных интегралов
- 13. Примеры. Исследовать на сходимость интегралы: 1) Ответ: несобственный интеграл сходится и равен 1(или сходится к 1)
- 14. 2) Ответ: несобственный интеграл стремится к бесконечности или расходится 27.11.2014
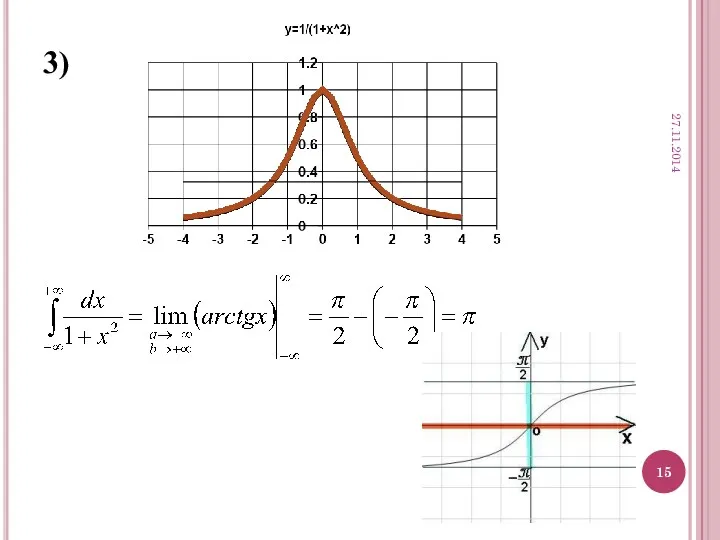
- 15. 3) 27.11.2014
- 16. Геометрический смысл несобственного интеграла I рода Несобственный интеграл выражает площадь БЕСКОНЕЧНО ДЛИННОЙ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ. 27.11.2014
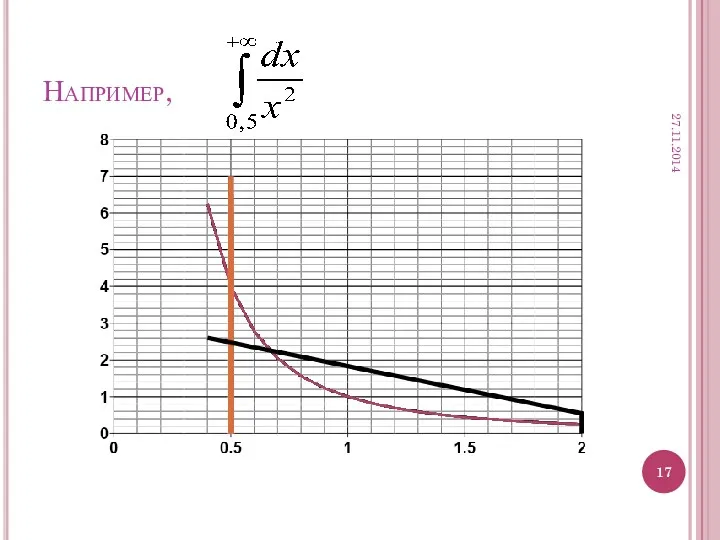
- 17. Например, 27.11.2014
- 18. Вычислим эту площадь: По определению получаем: 1) вычислим интеграл 27.11.2014
- 19. 2) Вычислим предел Ответ: несобственный интеграл т.е. сходится. Площадь бесконечно длинной криволинейной трапеции равна 2 27.11.2014
- 20. Признаки сходимости несобственных интегралов I рода Вопрос о сходимости несобственных интегралов усложняется, если первообразная функция неизвестна.
- 21. Признак сравнения 1. Пусть подынтегральная функция во всех точках интервала неотрицательна: и для всех значений выполняется
- 22. Пример Решить вопрос о сходимости интеграла Решение Так как при и интеграл сходится, то сходится и
- 23. Замечание Интеграл называется интегралом Пуассона и играет очень большую роль в теории вероятностей. 2. Сформулированный признак
- 24. Исследование интегралов от функций, не сохраняющих постоянный знак, например таких, как 27.11.2014
- 25. Признак сравнения 2. Если сходиться интеграл - интеграл от абсолютной величины функции , то сходится и
- 26. Замечание 1) Если сходится интеграл , то абсолютно сходятся и интегралы и , так как модули
- 27. Пример Интеграл Дирихле сходится, а интеграл (от модуля подынтегральной функции) расходится. Следовательно, интеграл Дирихле сходится условно.
- 28. Различие условно и абсолютно сходящихся несобственных интегралов установлено Дж. Стоксом и П. Г. Л. Дирихле в
- 29. Несобственные интегралы II рода Пусть функция имеет разрыв в точке Определение 1: несобственным интегралом от функции
- 30. Пусть функция имеет разрыв в точке Определение 2: несобственным интегралом от функции непрерывной в интервале и
- 31. Замечание Если первообразная функция известна, то в обоих случаях можно записать, что Где (или ) -
- 32. Точка разрыва функции находится внутри отрезка интегрирования Определение 3. Несобственным интегралом от функции , имеющей разрыв
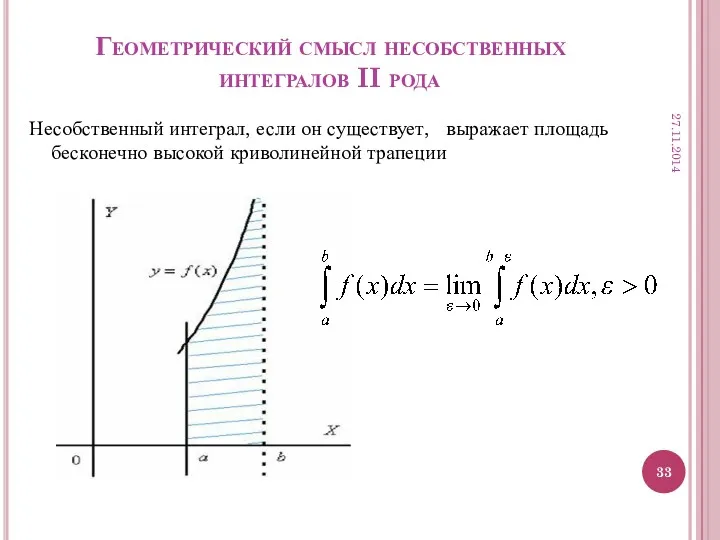
- 33. Геометрический смысл несобственных интегралов II рода Несобственный интеграл, если он существует, выражает площадь бесконечно высокой криволинейной
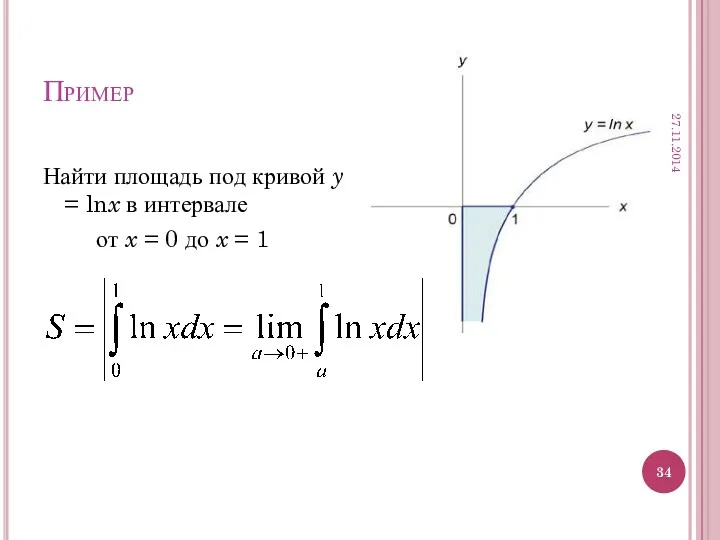
- 34. Пример Найти площадь под кривой y = lnx в интервале от x = 0 до x
- 35. Решение Преобразуем неопределённость вида Применим правило Лопиталя: Ответ: искомая площадь равна 27.11.2014
- 36. Замечание Признаки сходимости интегралов от функций с бесконечными разрывами подобны признакам сходимости несобственных интегралов I рода
- 37. Дополнение 1. На несобственные интегралы без всяких изменений переносятся простейшие свойства определённых интегралов 2. Основные приемы
- 38. 3. ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ Несобственные интегралы имеют большое значение во многих областях математического анализа и его приложений.
- 39. К несобственным интегралам относится и интеграл Фурье, а также интегралы, встречающиеся в др. интегральных преобразованиях. Решения
- 41. Скачать презентацию




















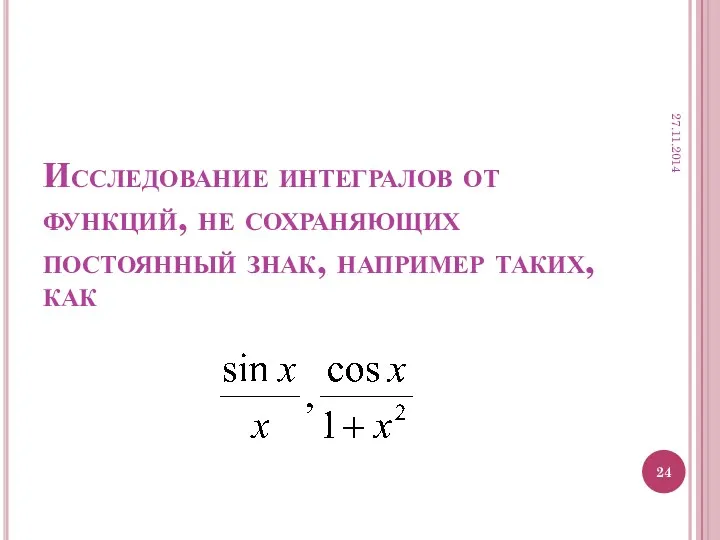













 Мультимедийная презентация урока по математике во 2 классе по учебнику М.И.Моро, М.А.Бантова Математика (система Школа России)(урок проведён в технологии деятельностного метода) тема: Письменный приём сложения двузначных чисе
Мультимедийная презентация урока по математике во 2 классе по учебнику М.И.Моро, М.А.Бантова Математика (система Школа России)(урок проведён в технологии деятельностного метода) тема: Письменный приём сложения двузначных чисе Дәрес планы
Дәрес планы 6.9
6.9 Геометрические фигуры, плоские и объемные
Геометрические фигуры, плоские и объемные Перпендикуляр и наклонная. Расстояние от точки до плоскости
Перпендикуляр и наклонная. Расстояние от точки до плоскости Золотий переріз
Золотий переріз Квадратный трёхчлен. 8 класс
Квадратный трёхчлен. 8 класс Сравнение чисел
Сравнение чисел Презентация Знакомимся с цифрами
Презентация Знакомимся с цифрами Параллельное проектирование. Изображение пространственных фигур
Параллельное проектирование. Изображение пространственных фигур Корень n-й степени. Упражнение 9
Корень n-й степени. Упражнение 9 Признаки делимости
Признаки делимости Математика о вреде курения (3). 6 класс
Математика о вреде курения (3). 6 класс Математический кружок Пифагор
Математический кружок Пифагор Тест по теме: Параллельность плоскостей
Тест по теме: Параллельность плоскостей Погрешности измерений. Классификация погрешностей
Погрешности измерений. Классификация погрешностей Математика вокруг нас
Математика вокруг нас Решение показательных неравенств
Решение показательных неравенств Математика вокруг нас для детей подготовительной к школе группы
Математика вокруг нас для детей подготовительной к школе группы Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Делители и кратные
Делители и кратные Интегрированный урок математики и информатики во 2 классе 1. Чугунова С. Учимся решать уравнения. М.: Эксмо. – 2011, 48 стр. 2. http://www.zachetka.ru/referat/preview.aspx?docid=26050&page=23 3. http://www.school2100.ru/upload/ib
Интегрированный урок математики и информатики во 2 классе 1. Чугунова С. Учимся решать уравнения. М.: Эксмо. – 2011, 48 стр. 2. http://www.zachetka.ru/referat/preview.aspx?docid=26050&page=23 3. http://www.school2100.ru/upload/ib Сложение и вычитание дробей с разными знаменателями. 6 класс
Сложение и вычитание дробей с разными знаменателями. 6 класс Усеченная пирамида
Усеченная пирамида Решение задач. Треугольники, часть 2
Решение задач. Треугольники, часть 2 Задачи, приводящие к понятию определенного интеграла
Задачи, приводящие к понятию определенного интеграла Учебно - методическое пособие Математический коврик
Учебно - методическое пособие Математический коврик Угол между векторами. Скалярное произведение
Угол между векторами. Скалярное произведение