Содержание
- 2. Лекция Обратные тригонометрические функции
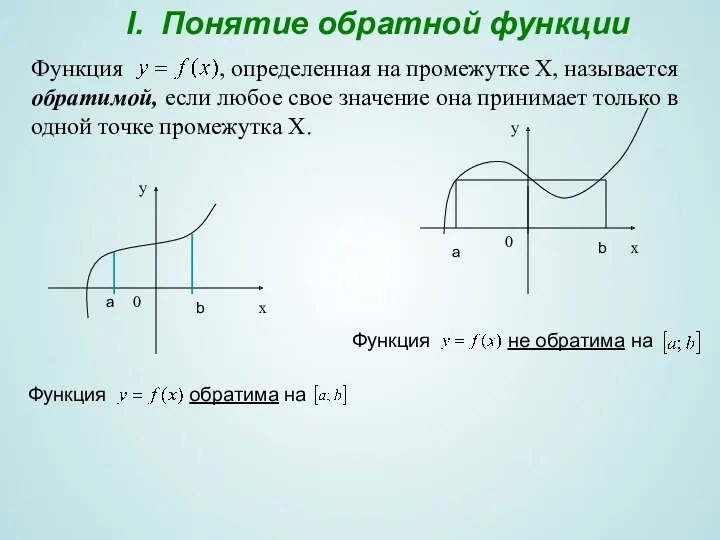
- 3. I. Понятие обратной функции Функция , определенная на промежутке Х, называется обратимой, если любое свое значение
- 4. Теорема. Если функция строго монотонна на промежутке Х, то она обратима на этом промежутке. Доказательство. Пусть
- 5. Пусть обратимая функция определена на промежутке Х, а областью значений ее является промежуток Y. Поставим в
- 6. Алгоритм получения обратной функции 1) Убедиться в том, что функция обратима на Х. 2) Из уравнения
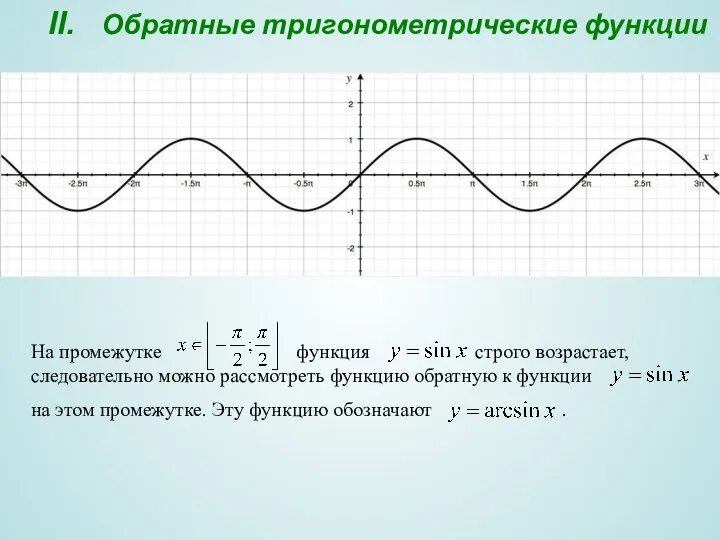
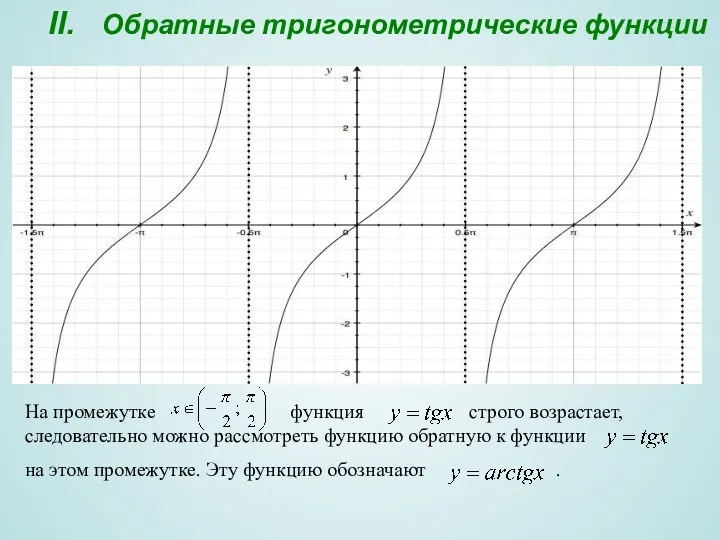
- 7. II. Обратные тригонометрические функции На промежутке функция строго возрастает, следовательно можно рассмотреть функцию обратную к функции
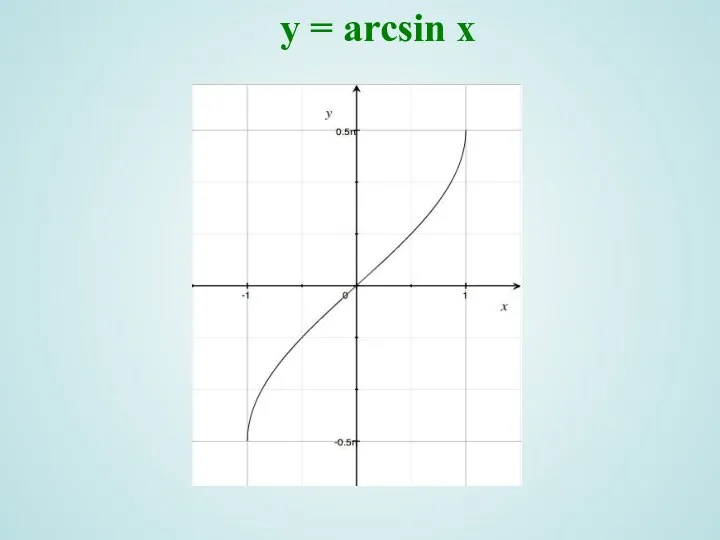
- 8. y = arcsin x
- 9. y = arcsin x Область определения ; , 2) Область значений ; 3) Функция нечетная arcsin
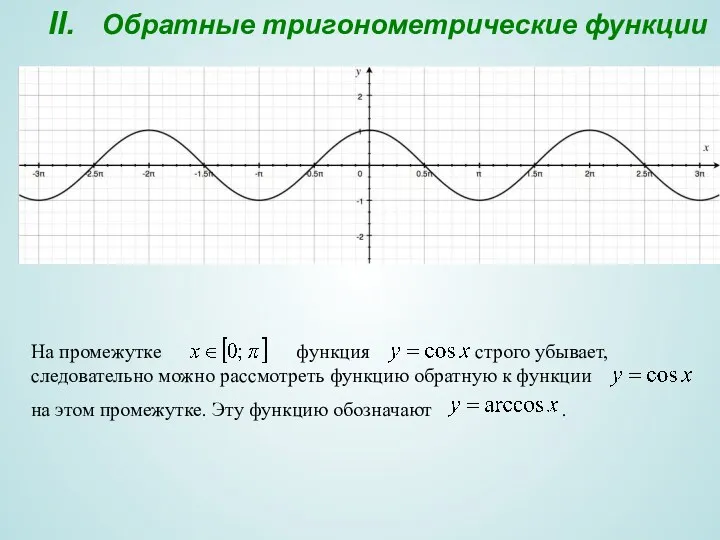
- 10. II. Обратные тригонометрические функции На промежутке функция строго убывает, следовательно можно рассмотреть функцию обратную к функции
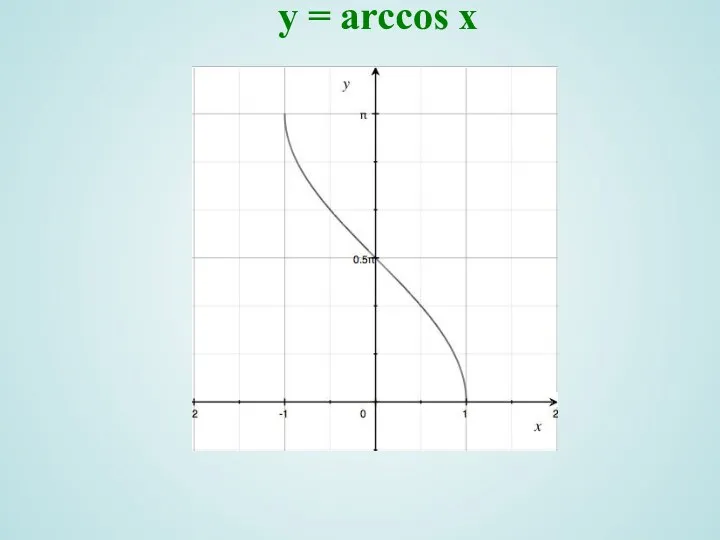
- 11. y = arccos x
- 12. y = arccos x Область определения ; , 2) Область значений ; 3) Функция не обладает
- 13. II. Обратные тригонометрические функции На промежутке функция строго возрастает, следовательно можно рассмотреть функцию обратную к функции
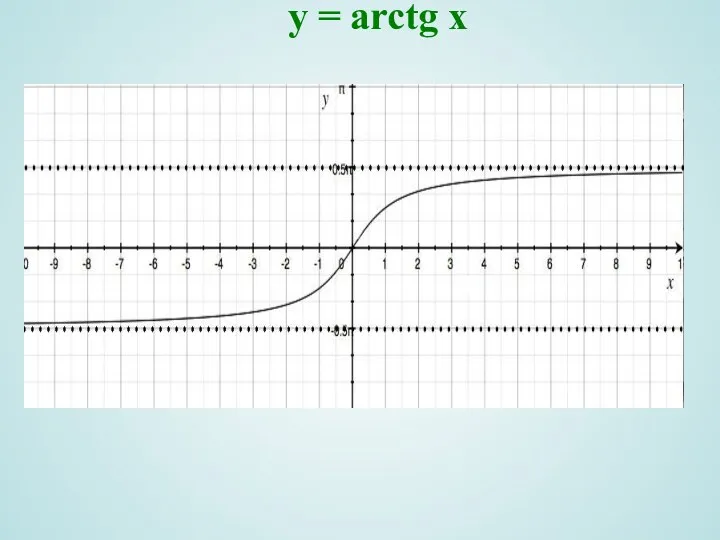
- 14. y = arctg x
- 15. y = arctg x Область определения D(y)=R ; , 2) Область значений ; 4) Функция непериодическая
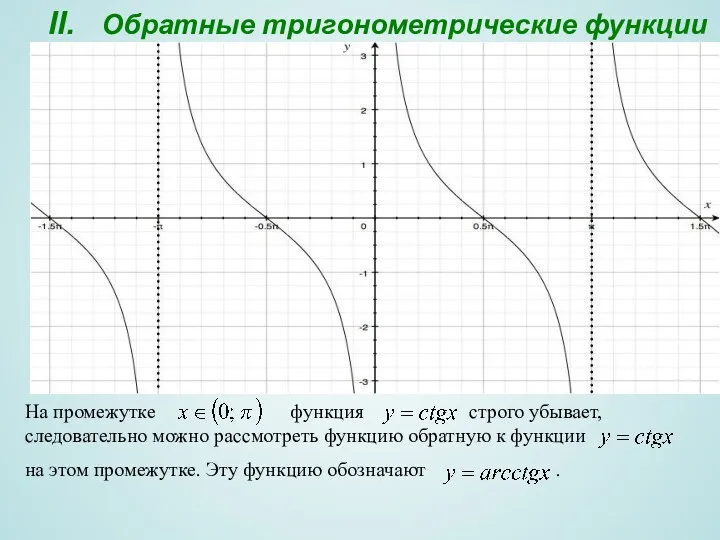
- 16. II. Обратные тригонометрические функции На промежутке функция строго убывает, следовательно можно рассмотреть функцию обратную к функции
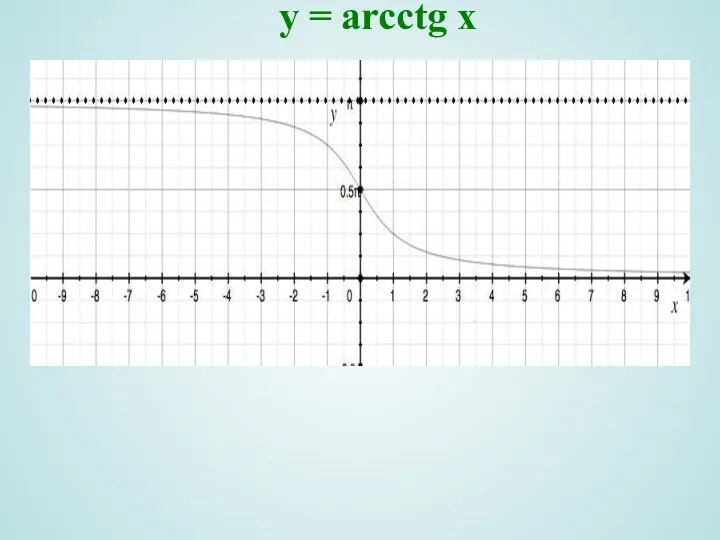
- 17. y = arcctg x
- 18. y = arcсtg x Область определения D(y)=R ; , 2) Область значений ; 4) Функция непериодическая
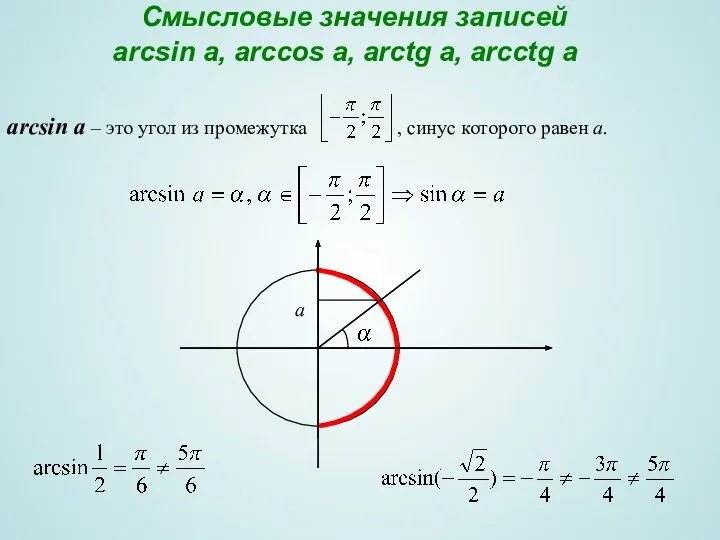
- 19. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrcsin a – это угол
- 20. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrccos a – это угол
- 21. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrctg a – это угол
- 22. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrcсtg a – это угол
- 24. Скачать презентацию











 Угол между плоскостями
Угол между плоскостями Презентация к уроку математики в 4 классе.
Презентация к уроку математики в 4 классе. Измерение углов. Транспортир
Измерение углов. Транспортир Краткие теоретические сведения. Планиметрия
Краткие теоретические сведения. Планиметрия Решение показательных уравнений
Решение показательных уравнений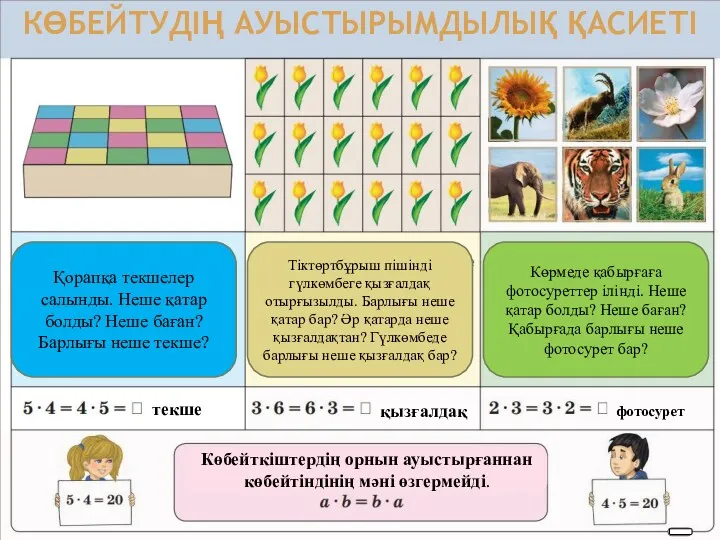 Көбейтудің ауыстырымдылық қасиеті
Көбейтудің ауыстырымдылық қасиеті Определение числовой функции и способы её задания
Определение числовой функции и способы её задания Векторы в пространстве
Векторы в пространстве Насекомые
Насекомые Численное решение систем линейных алгебраических уравнений СЛАУ
Численное решение систем линейных алгебраических уравнений СЛАУ Вероятность и статистика. 7 класс
Вероятность и статистика. 7 класс Тригонометрия. Углы
Тригонометрия. Углы Деление натуральных чисел. 5 класс
Деление натуральных чисел. 5 класс Сумма углов треугольника
Сумма углов треугольника Математическая статистика
Математическая статистика Свойства корня n-й степени
Свойства корня n-й степени Умножение и деление на 3. Треть числа.
Умножение и деление на 3. Треть числа. Dreapta. Matematică
Dreapta. Matematică Теория вероятностей в заданиях ЕГЭ
Теория вероятностей в заданиях ЕГЭ Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Устный счет в пределах 10
Устный счет в пределах 10 Первый признак равенства треугольников
Первый признак равенства треугольников Вычитание вида 1718-
Вычитание вида 1718- Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Смешанные числа. Математика — царица наук
Смешанные числа. Математика — царица наук Единицы измерения площадей
Единицы измерения площадей Совместные действия с рациональными числами
Совместные действия с рациональными числами Колмогоров - Смирнов келісім критерийі
Колмогоров - Смирнов келісім критерийі