Содержание
- 2. Определенный интеграл, как предел интегральной суммы Пусть функция y = f(x) определена на отрезке [a; b].
- 3. Составим сумму всех таких произведений Если при этом интегральная сумма Sn имеет предел I, который не
- 4. Теорема (существования определенного интеграла) [a; b] - область (отрезок) интегрирования Непрерывность функции является достаточным условием ее
- 5. Геометрический смысл определенного интеграла Пусть непрерывная неотрицательная функция y = f(x) задана на отрезке [a; b].
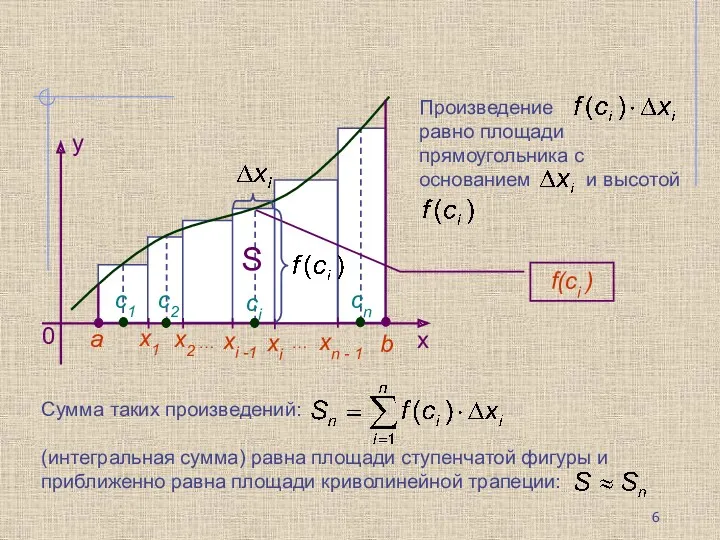
- 6. … … f(ci ) S
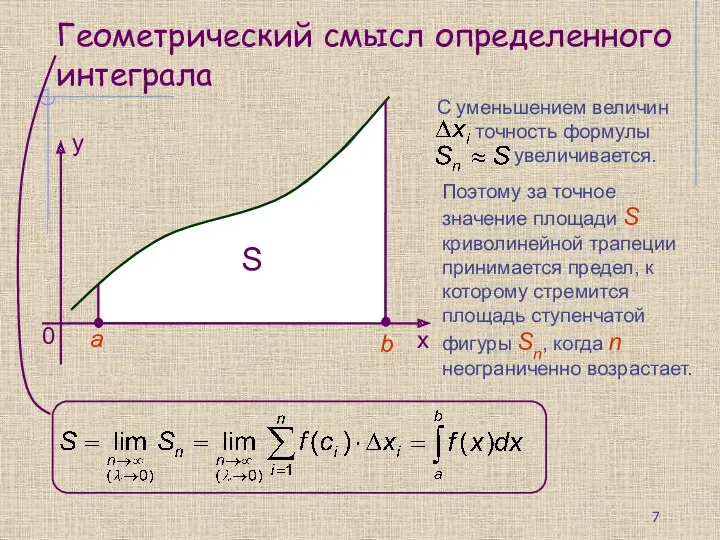
- 7. Геометрический смысл определенного интеграла Поэтому за точное значение площади S криволинейной трапеции принимается предел, к которому
- 8. Физический смысл определенного интеграла … … Сила, действующая на отрезке [xi - 1; xi] меняется от
- 9. Точное значение работы А : Аналогично можно показать, что путь S, пройденный точкой за промежуток времени
- 10. Формула Ньютона - Лейбница Теорема Если функция y = f(x) непрерывна на отрезке [a; b] и
- 11. Свойства определенного интеграла Если функция f интегрируема на каждом из отрезков [a, c] и [c, b]
- 12. Теорема о среднем Это свойство имеет при f(x) > 0 следующий геометрический смысл: Значение определенного интеграла
- 13. Если функция f сохраняет знак на отрезке [a, b] то интеграл на этом отрезке имеет тот
- 14. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим
- 15. Замена переменной в определенном интеграле Теорема Если: Замечания: 1) при вычислении определенного интеграла методом подстановки возвращаться
- 16. Пример.
- 18. Скачать презентацию


![Теорема (существования определенного интеграла) [a; b] - область (отрезок) интегрирования](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/198905/slide-3.jpg)






![Если функция f сохраняет знак на отрезке [a, b] то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/198905/slide-12.jpg)



 Презентация: Развитие познавательных и творческих способностей через систему логических и математических игр
Презентация: Развитие познавательных и творческих способностей через систему логических и математических игр Элементы теории вероятности и математической статистики
Элементы теории вероятности и математической статистики Статистические оценки параметров распределения. Доверительные интервалы
Статистические оценки параметров распределения. Доверительные интервалы Симметрия вокруг нас
Симметрия вокруг нас Точки, прямые, отрезки. 7 класс
Точки, прямые, отрезки. 7 класс Начальные сведения стереометрии
Начальные сведения стереометрии Скалярное произведение векторов
Скалярное произведение векторов Using first derivative. Using second derivative
Using first derivative. Using second derivative Вычисление площадей многоугольников с использованием формулы Пика
Вычисление площадей многоугольников с использованием формулы Пика Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников Средства измерений. Метрологические характеристики. Метрологические характеристики средств измерений
Средства измерений. Метрологические характеристики. Метрологические характеристики средств измерений Презентация к уроку математикиАрифметические Действия над числами урок 19 программа Школа 2100
Презентация к уроку математикиАрифметические Действия над числами урок 19 программа Школа 2100 Математика в ребусах, загадках и кроссвордах
Математика в ребусах, загадках и кроссвордах Ряды
Ряды Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Смежные и вертикальные углы, их свойства
Смежные и вертикальные углы, их свойства Арксинус. Решение уравнения sin t = a
Арксинус. Решение уравнения sin t = a Теория вероятностей; геометрическая вероятность; неравенство Чебышева
Теория вероятностей; геометрическая вероятность; неравенство Чебышева Правильные многоугольники
Правильные многоугольники Единицы длины. Закрепление пройденного материала
Единицы длины. Закрепление пройденного материала Сфера. Шар. Части сферы и шара
Сфера. Шар. Части сферы и шара Подобие треугольников. Признаки подобия треугольников (8 класс)
Подобие треугольников. Признаки подобия треугольников (8 класс) Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Графический диктант 6. 5 класс
Графический диктант 6. 5 класс Вектор - направленный отрезок
Вектор - направленный отрезок Функции в математике и в жизни. Математика вокруг нас
Функции в математике и в жизни. Математика вокруг нас Математик кичә
Математик кичә Формулы корней квадратных уравнений
Формулы корней квадратных уравнений