Содержание
- 2. Lecture Outline Using first derivative Increasing/ decreasing intervals Critical points Stationary points First derivative test Using
- 3. Introduction The purpose of this lecture is to develop mathematical tools that can be used to
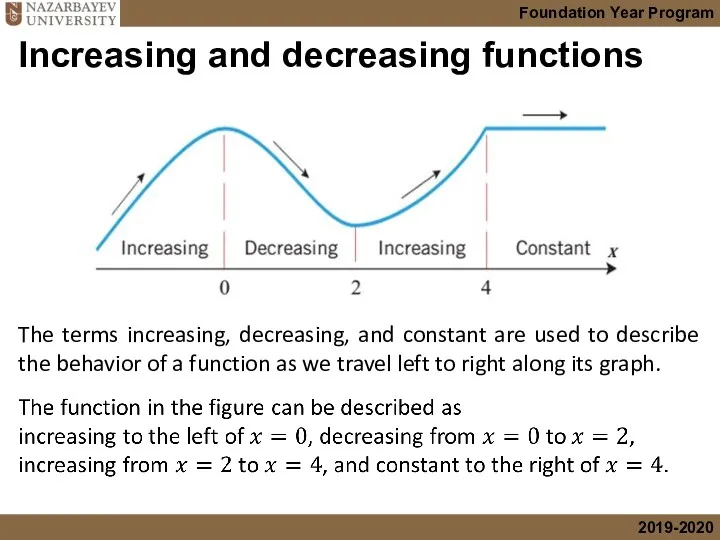
- 4. Increasing and decreasing functions The terms increasing, decreasing, and constant are used to describe the behavior
- 5. Increasing and decreasing functions
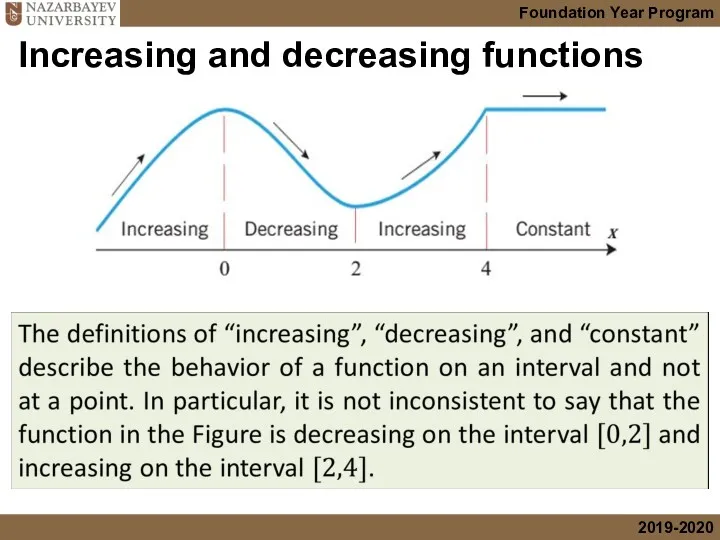
- 6. Increasing and decreasing functions
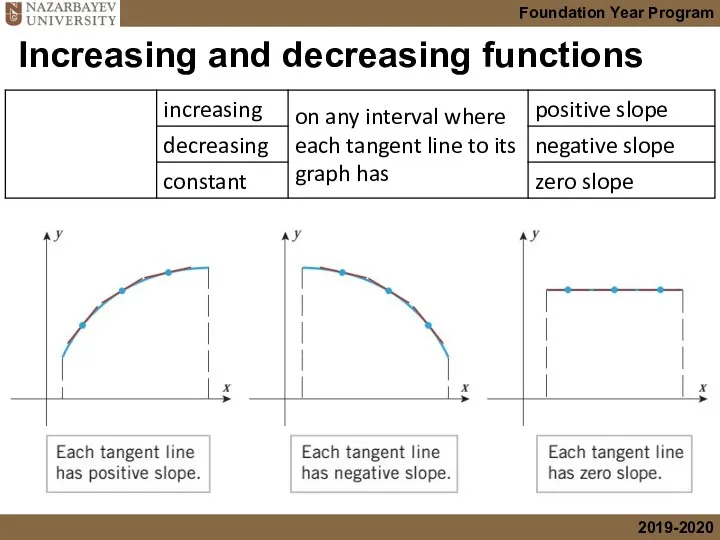
- 7. Increasing and decreasing functions
- 8. Increasing and decreasing functions
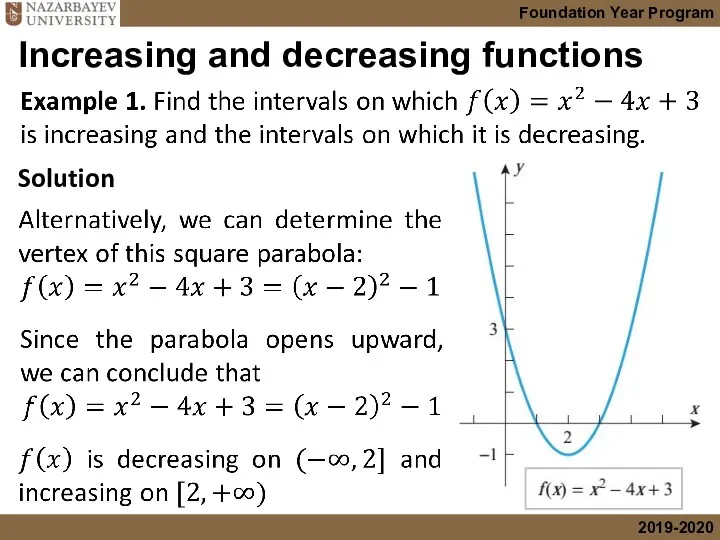
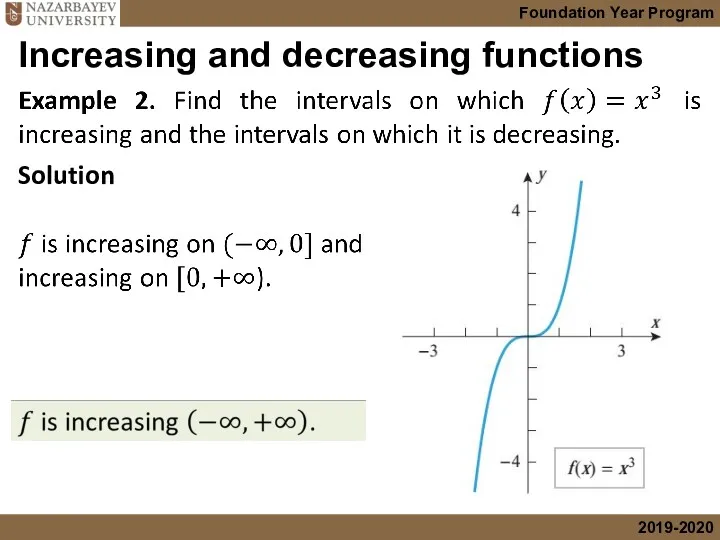
- 9. Increasing and decreasing functions Solution
- 10. Increasing and decreasing functions Solution
- 11. Increasing and decreasing functions Solution
- 12. Increasing and decreasing functions Solution
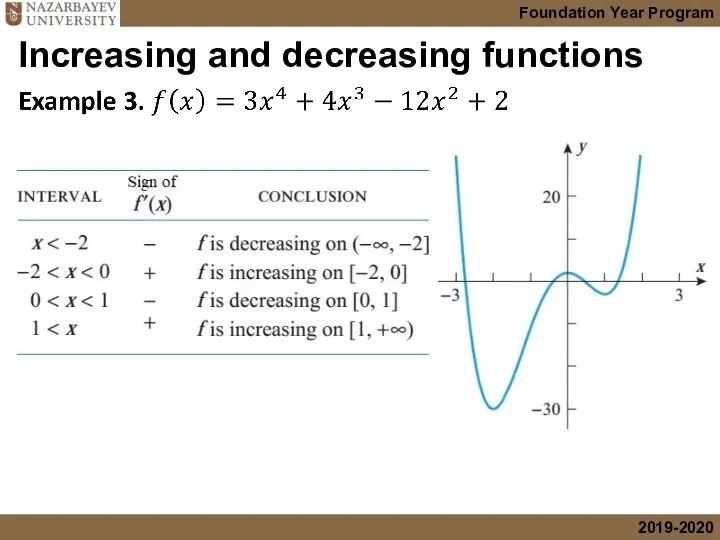
- 13. Increasing and decreasing functions Solution Differentiating f we obtain
- 14. Increasing and decreasing functions Solution Constructing a following table we conclude:
- 15. Increasing and decreasing functions
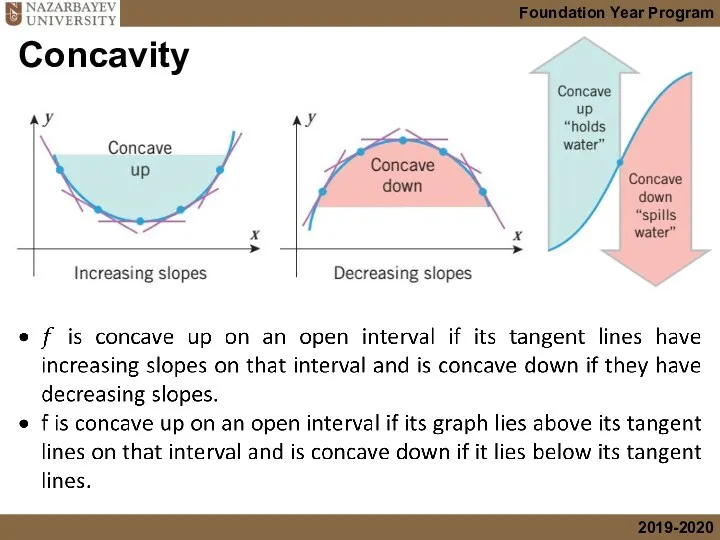
- 16. Concavity
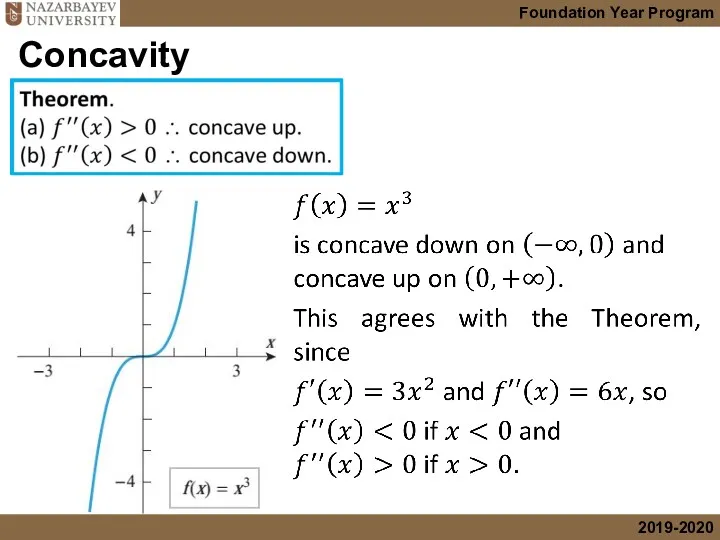
- 17. Concavity
- 18. Concavity
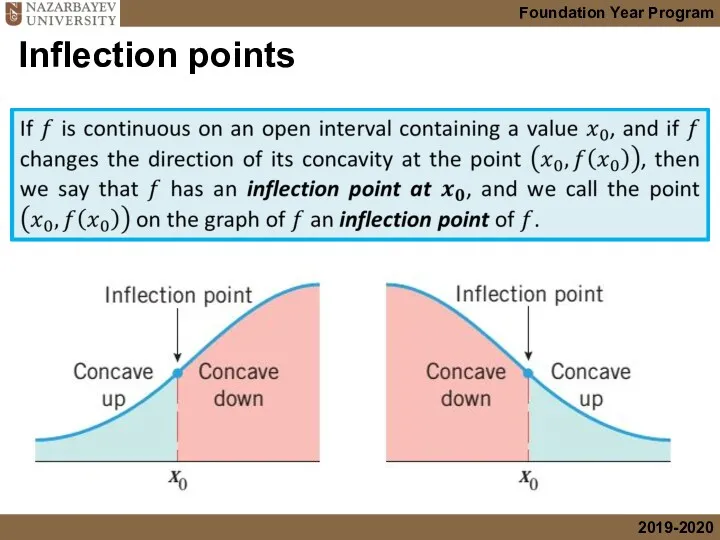
- 19. Inflection points
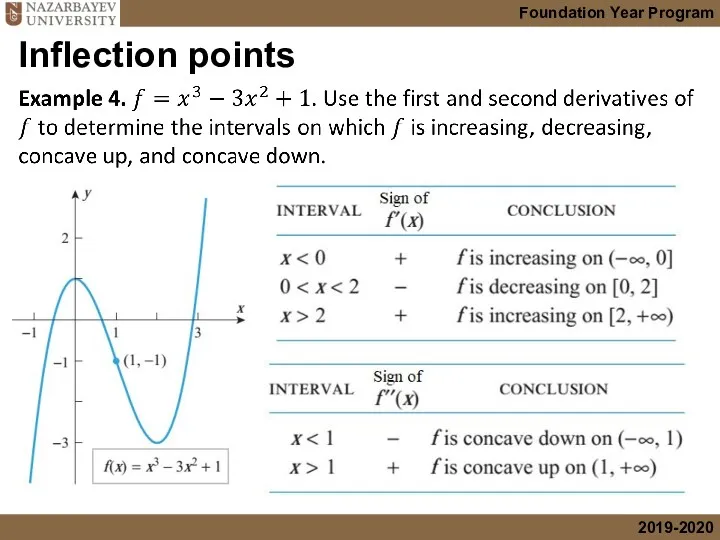
- 20. Inflection points Solution
- 21. Inflection points Solution
- 22. Inflection points
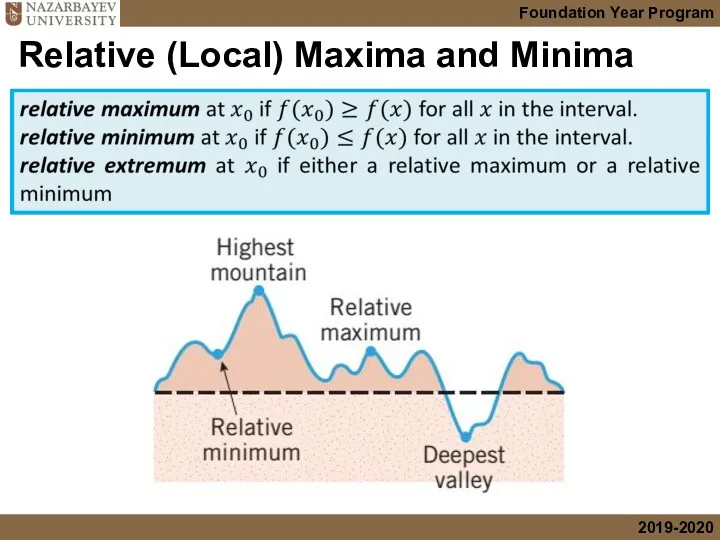
- 23. Relative (Local) Maxima and Minima
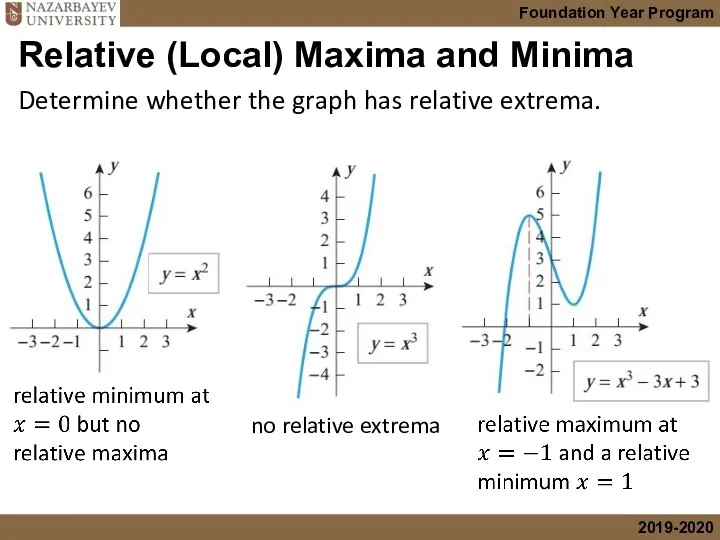
- 24. Relative (Local) Maxima and Minima
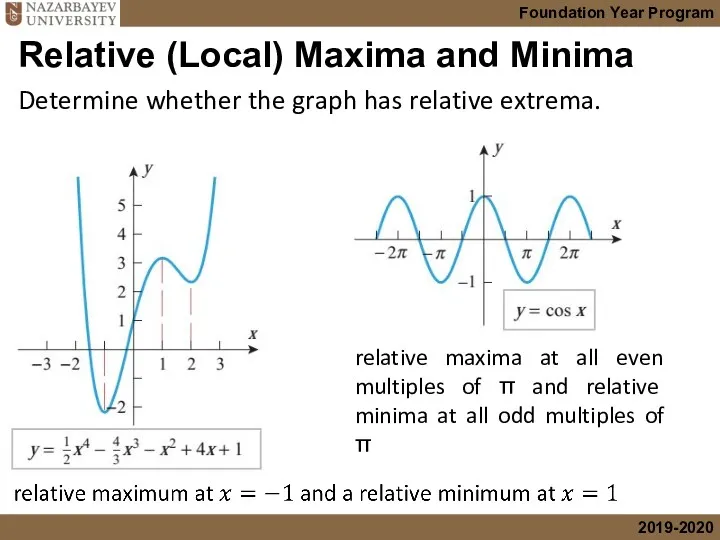
- 25. no relative extrema Relative (Local) Maxima and Minima Determine whether the graph has relative extrema.
- 26. relative maxima at all even multiples of π and relative minima at all odd multiples of
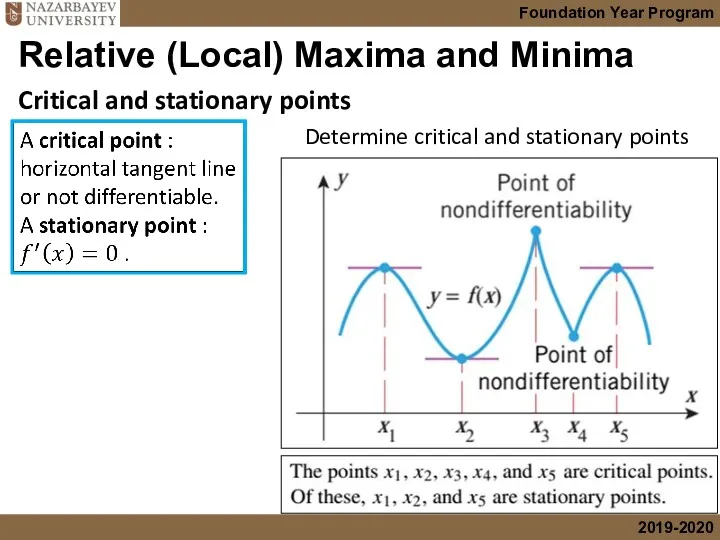
- 27. Critical and stationary points Relative (Local) Maxima and Minima
- 28. Critical and stationary points Relative (Local) Maxima and Minima Determine critical and stationary points
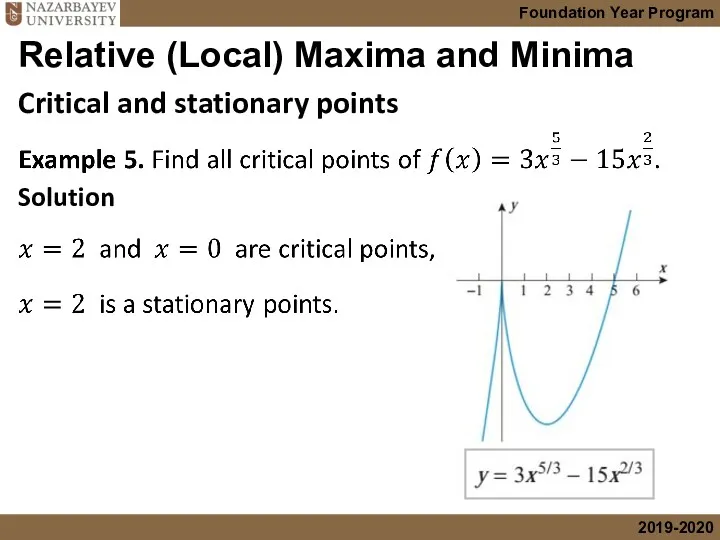
- 29. Relative (Local) Maxima and Minima Critical and stationary points
- 30. Relative (Local) Maxima and Minima Critical and stationary points Solution The function f is continuous everywhere
- 31. Relative (Local) Maxima and Minima Critical and stationary points Solution
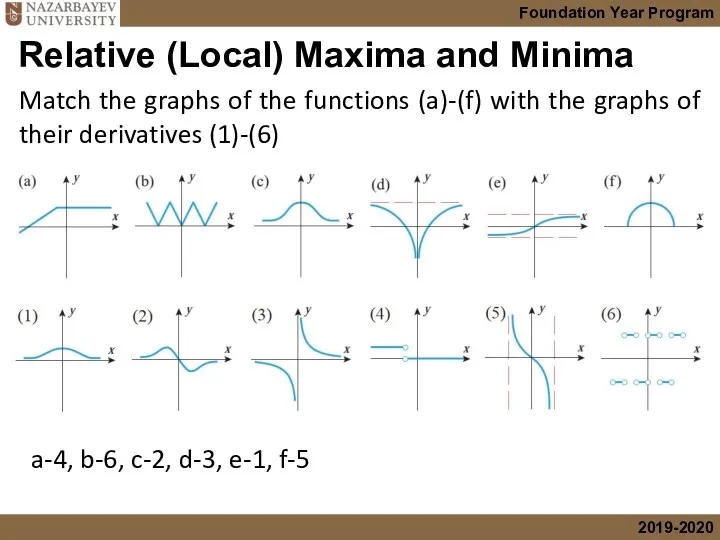
- 32. Relative (Local) Maxima and Minima Match the graphs of the functions (a)-(f) with the graphs of
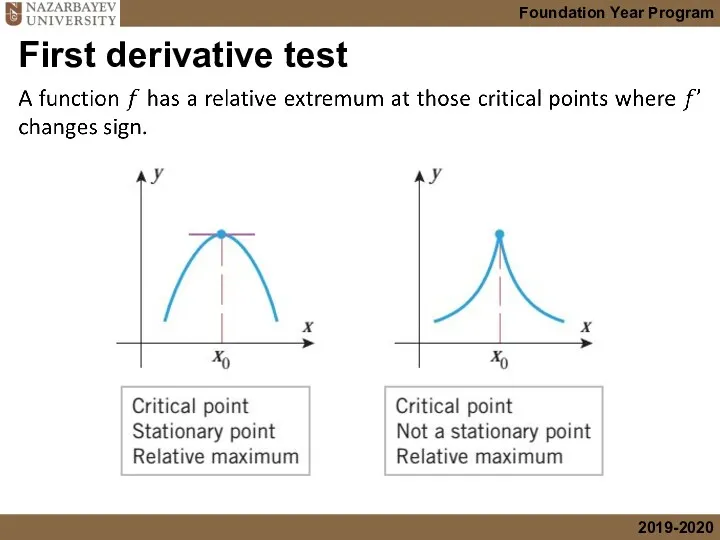
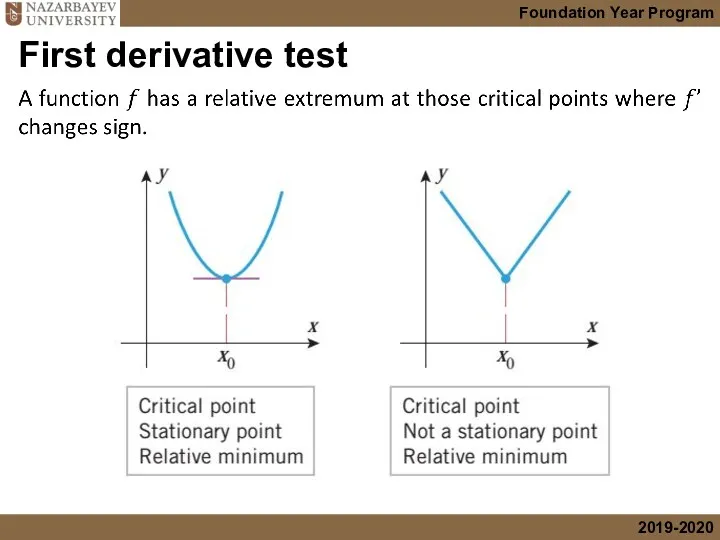
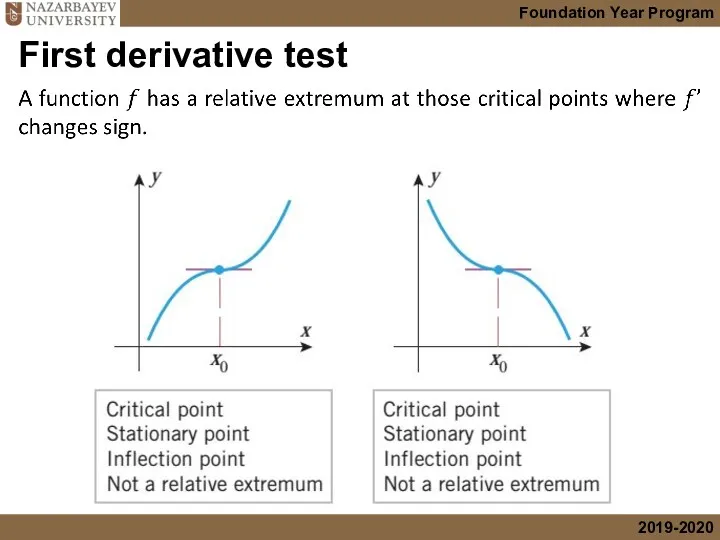
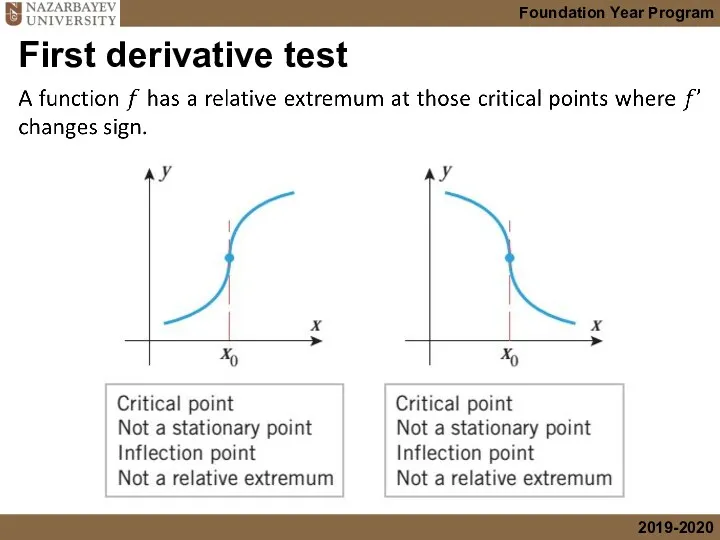
- 33. First derivative test
- 34. First derivative test
- 35. First derivative test
- 36. First derivative test
- 37. First derivative test
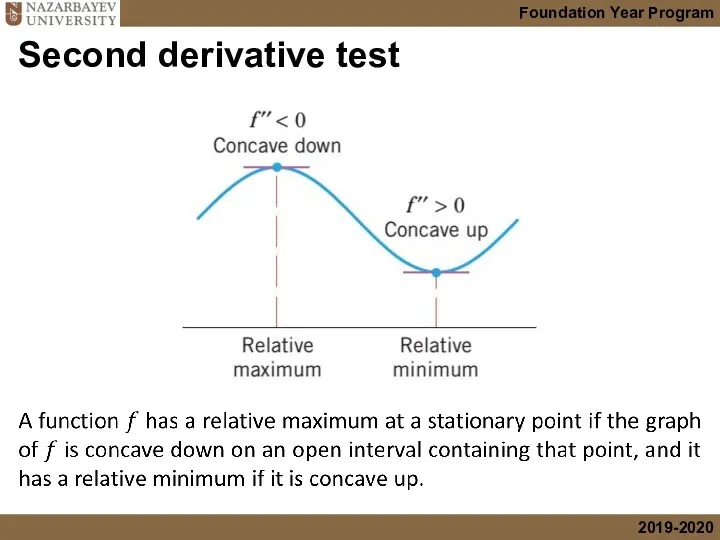
- 38. Second derivative test
- 39. Second derivative test
- 40. Second derivative test Solution We have Implement the Second derivative test:
- 41. Second derivative test Solution
- 42. Second derivative test Solution
- 43. Learning outcomes 5.3.1. Define stationary points of a function. 5.3.2. Define intervals on which a function
- 44. Formulae
- 45. Formulae
- 47. Скачать презентацию























 Преобразования графиков функций
Преобразования графиков функций Прогрессии вокруг нас
Прогрессии вокруг нас Математические методы и модели исследования операций. Этапы математического моделирования
Математические методы и модели исследования операций. Этапы математического моделирования Решение заданий ЕГЭ В6 (часть 1)
Решение заданий ЕГЭ В6 (часть 1) Арксинус, арккосинус, арктангенс и арккотангенс. Алгебра и начало анализа 10 класс
Арксинус, арккосинус, арктангенс и арккотангенс. Алгебра и начало анализа 10 класс Производная и ее применения
Производная и ее применения Большая математическая мастерская
Большая математическая мастерская Уравнение и его корни. Алгебра 7 класс
Уравнение и его корни. Алгебра 7 класс Объемы. Соотношения между единицами объема
Объемы. Соотношения между единицами объема Площадь круга и кругового сектора
Площадь круга и кругового сектора Произведение многочленов
Произведение многочленов Способы решения задачи
Способы решения задачи Соотношение между углами и сторонами треугольника
Соотношение между углами и сторонами треугольника Понятие положительной скалярной величины и ее измерения
Понятие положительной скалярной величины и ее измерения Элементы теории графов. Тема 2
Элементы теории графов. Тема 2 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Простые дроби
Простые дроби Нахождение расстояния между двумя точками на координатной прямой
Нахождение расстояния между двумя точками на координатной прямой Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы
Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы Тренажер по математике для учащихся 1 класса Приключение богатырей
Тренажер по математике для учащихся 1 класса Приключение богатырей Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов Интерактивный плакат Геометрические фигуры. 1-4 класс
Интерактивный плакат Геометрические фигуры. 1-4 класс Натуральные числа и шкалы
Натуральные числа и шкалы Vectors and the geometry of space
Vectors and the geometry of space Формирование знаний и умений вычисления периметра многоугольников.
Формирование знаний и умений вычисления периметра многоугольников. Название компонентов и результата действия деления. 2 класс
Название компонентов и результата действия деления. 2 класс Десятичные дроби. 5 класс
Десятичные дроби. 5 класс