Слайд 2
![ОПРЕДЕЛЕНИЕ Пусть на отрезке [a,b] задана функция y = f(x).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/176796/slide-1.jpg)
ОПРЕДЕЛЕНИЕ
Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 ,x2], …,
[xi-1 , xi], …, [xn-1 , xn]; длину i-го отрезка обозначим : ; максимальную из длин отрезков обозначим . На каждом из отрезков[xi-1 , xi] выберем произвольную точку и составим сумму .
Сумма называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм при , не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек , то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функцииf(x) по отрезку [a,b] и обозначается .
Слайд 3
![ГЕОМЕТРИЧЕСКИЙ СМЫСЛ если f(x) >0 на отрезке [a,b], то равен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/176796/slide-2.jpg)
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
если f(x) >0 на отрезке [a,b], то равен площади криволинейной трапецииABCD, ограниченной снизу отрезком [a,b], слева
и справа - прямыми x = a и x = b, сверху – функцией y = f(x).
Слайд 4
![ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА Если f(x) непрерывна на отрезке [a, b], и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/176796/slide-3.jpg)
ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то .
Док-во. Мы установили, что
функция - первообразная непрерывной f(x). Так как F(x) - тоже первообразная, то Ф(x) = F(x) + C. Положим в этом равенстве x =a. Так как , то . В равенстве переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x , верхний предел x обозначим b. Окончательно, .
Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом: (здесь читается как “ подстановка от a до b"), поэтому формулу Ньютона-Лейбница обычно записывают так: .
Слайд 5

Если u(x), v(x) - непрерывно дифференцируемые функции, то
Док-во. Интегрируем равенство в пределах от a до b: . Функция в
левом интеграле имеет первообразную uv, по формуле Ньютона-Лейбница ,
откуда и следует доказываемое равенство.
Пример:
Слайд 6

ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЁННОМ ИНТЕГРАЛЕ.
Пусть функция
определена, непрерывно дифференцируема и монотонна на
отрезке ,
,
функция непрерывна на отрезке [a, b].
Тогда
![ОПРЕДЕЛЕНИЕ Пусть на отрезке [a,b] задана функция y = f(x).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/176796/slide-1.jpg)
![ГЕОМЕТРИЧЕСКИЙ СМЫСЛ если f(x) >0 на отрезке [a,b], то равен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/176796/slide-2.jpg)
![ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА Если f(x) непрерывна на отрезке [a, b], и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/176796/slide-3.jpg)


 Математика. 1 класс. Урок 88. Табличное сложение - Презентация
Математика. 1 класс. Урок 88. Табличное сложение - Презентация Функции в жизни человека
Функции в жизни человека Функция y=f (x)
Функция y=f (x) Фигуры: плоские и объёмные
Фигуры: плоские и объёмные Дециметр
Дециметр Подобные треугольники (8 класс)
Подобные треугольники (8 класс)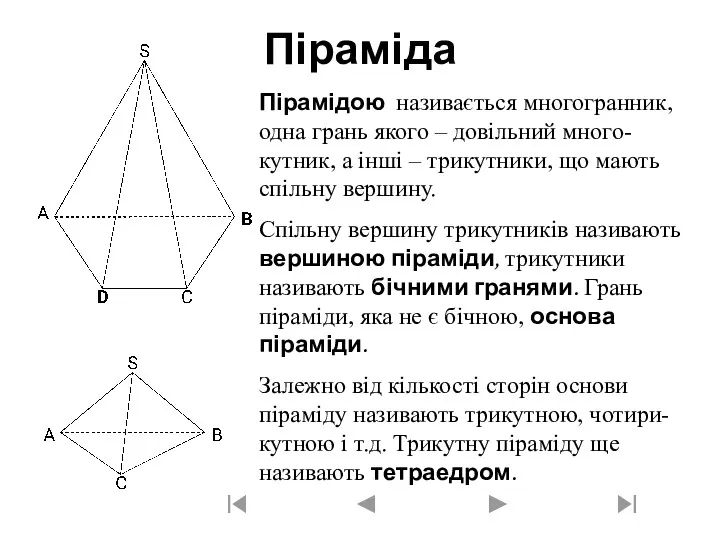 Многогранник піраміда
Многогранник піраміда Своя игра. Внеклассное мероприятие по математике
Своя игра. Внеклассное мероприятие по математике Математика. 2 класс. Школа России. Тема Закрепление. Решение задач
Математика. 2 класс. Школа России. Тема Закрепление. Решение задач Прямоугольник. Квадрат 2 класс
Прямоугольник. Квадрат 2 класс Приемы устных вычислений вида 450+30, 620-200
Приемы устных вычислений вида 450+30, 620-200 Тригонометрические формулы
Тригонометрические формулы Путешествие на планету математика
Путешествие на планету математика Взаимное расположение прямой и окружности. 8 класс
Взаимное расположение прямой и окружности. 8 класс презентация единицы времени
презентация единицы времени Сложение чисел с разными знаками. 6 класс
Сложение чисел с разными знаками. 6 класс Многочлены
Многочлены Штей сызылған бұрыш туралы теорема
Штей сызылған бұрыш туралы теорема Уравнения
Уравнения Динамическое программирование. (Лекция 3)
Динамическое программирование. (Лекция 3) Параллельность прямых, прямой и плоскости
Параллельность прямых, прямой и плоскости История происхождения дробей в разных странах
История происхождения дробей в разных странах Урок математики в 1 классе. Уменьшаемое. Вычитаемое. Разность
Урок математики в 1 классе. Уменьшаемое. Вычитаемое. Разность Логарифмические неравенства
Логарифмические неравенства Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел Основы квалиметрии. Общие сведения о методологии квалиметрии
Основы квалиметрии. Общие сведения о методологии квалиметрии Перестановки, размещения, сочетания
Перестановки, размещения, сочетания Математика в школе и жизни. Элементы статистики
Математика в школе и жизни. Элементы статистики