Содержание
- 2. Содержание РАЗДЕЛ 1. Основания математики (задача 1) РАЗДЕЛ 2. Элементы линейной алгебры и аналитической геометрии (задачи
- 3. § 1. Элементы теории графов Раздел 1. Основания математики
- 4. Определение. Граф - это упорядоченная пара G = G(V, E), где V ≠ ∅ - непустое
- 5. Примеры графов:
- 6. ОТНОШЕНИЯ МЕЖДУ ВЕРШИНАМИ И РЕБРАМИ 1) Две вершины графа называются смежными, если существует соединяющее их ребро.
- 7. Определение. Число рёбер, инцидентных вершине v, называется степенью этой вершины и обозначается Если степень вершины равна
- 8. На рисунке вершина А имеет степень, равную 1, вершина С – 4, вершина D – 2.
- 9. Способы задания графа 1) Матрица инцидентности - таблица, состоящая из n строк (вершины) и т столбцов
- 10. 2) Матрица смежности графа - квадратная таблица А порядка n, в которой: равно количеству ребер, соединяющих
- 11. Пример. Граф, имеет матрицу инциденций. Построить граф и найти матрицу смежности Решение .
- 12. Раздел 2. Элементы линейной алгебры и аналитической геометрии § 1. Матрицы. Операции над ними. § 2.
- 13. ОПРЕДЕЛЕНИЕ. Матрицей называется прямоугольная таблица из m строк и n столбцов, содержащая числа или иные математические
- 14. ВИДЫ МАТРИЦ
- 15. 4) Квадратная матрица называется единичной, если ее элементы, расположенные на главной диагонали, равны единице, остальные –
- 16. 6) Квадратная матрица называется диагональной, если элементы, стоящие вне главной диагонали равны нулю 7) Квадратная матрица
- 17. Действия над матрицами Равенство матриц Сложение (вычитание) матриц Сумма и разность матриц существуют только для матриц
- 18. Умножение матрицы на число Найти значение выражения: При умножении матрицы A на число k получается матрица
- 19. Умножение матриц Произведение матриц A * B определено только тогда, когда число столбцов матрицы А равно
- 20. Пример. Найти С = A * B 6 9 1 14 24 4
- 21. 2) Определитель 2 - го порядка. § 2. Определители. Определитель (обозначается )– это числовая характеристика квадратных
- 22. a11a22a33+a12a23a31+ a13a21a32- - a13a22a31- a21a12a33- a32a23a11 «+» «-» 3) Определитель 3 - го порядка. Правило треугольников.
- 23. Метод треугольника применим только для определителей 3 порядка Пример.
- 24. Правило Лапласа (разложение по элементам строки (столбца) 3) Определитель n - го порядка. Определитель n-го порядка
- 25. Пример.
- 26. Свойства определителя n-го порядка: 1. Определитель матрицы А равен определителю транспонированной матрицы, т.е. 2. Если все
- 27. 7. Значение определителя не изменится, если к элементам его некоторой строки прибавить соответствующие элементы другой строки,
- 28. §3. Обратная матрица Теорема. Обратная матрица существует и единственна тогда и только тогда, когда . Определение.
- 29. §4. Метод обратной матрицы решения систем линейных уравнений Метод обратной матрицы рассмотрим на примере решения квадратной
- 30. Тогда систему можно записать так: Найдем решение системы в матричном виде. Предположим, что det A отличен
- 31. Метод обратной матрицы решения систем линейных уравнений Решить систему методом обратной матрицы. -0,5 2 -5
- 32. §5. Метод Крамера. Рассмотрим систему из трех уравнений с тремя неизвестными: Δ- главный определитель системы. Рассмотрим
- 33. Теорема (правило Крамера). Тогда, если , система линейных уравнение имеет единственное решение, определяемое по формулам Крамера:
- 34. Пример: Решить систему уравнений по формулам Крамера. значит система имеет единственное решение, определяемое формулами Крамера
- 35. Рассмотрим систему линейных уравнений где числа а11, а12,…а33 – коэффициенты системы, b1, b2,b3 - свободные члены
- 36. Метод Гаусса решения систем линейных уравнений Следующие действия над расширенной матрицей системы называются элементарными преобразованиями. Умножение
- 37. Пример: Решить систему уравнений методом Гаусса. Расширенная матрица системы имеет вид: Переставим строки (для удобства): От
- 39. Скачать презентацию
 Кути. Трикутники. Підготовка до ЗНО
Кути. Трикутники. Підготовка до ЗНО Промысловые рыбы (математика, 3 класс, УМК Планета знаний)
Промысловые рыбы (математика, 3 класс, УМК Планета знаний) Тесты для интерактивной доски по УМК Школа России
Тесты для интерактивной доски по УМК Школа России Решение квадратных уравнений
Решение квадратных уравнений Правильные многогранники. Геометрия 10 класс
Правильные многогранники. Геометрия 10 класс математика. Деление.
математика. Деление. 7 способов решения тригонометрического уравнения, или еще раз о красоте математики
7 способов решения тригонометрического уравнения, или еще раз о красоте математики Метод математических моделей в экономике
Метод математических моделей в экономике Конспект урока по математике по теме Урок- путешествие в космос. Закрепление знаний таблицы сложения с переходом через десяток.1 класс.
Конспект урока по математике по теме Урок- путешествие в космос. Закрепление знаний таблицы сложения с переходом через десяток.1 класс. Метод интервалов в решении рациональных неравенств
Метод интервалов в решении рациональных неравенств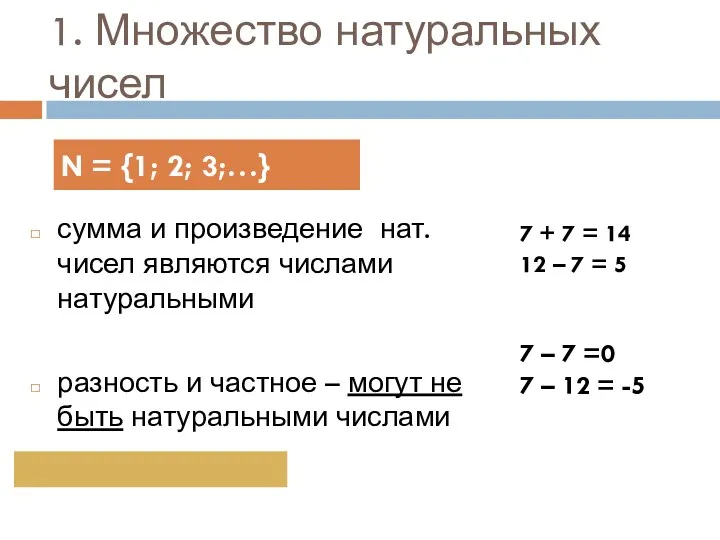 Множество натуральных чисел
Множество натуральных чисел Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Приёмы устных вычислений типа 560-90, 470+80
Приёмы устных вычислений типа 560-90, 470+80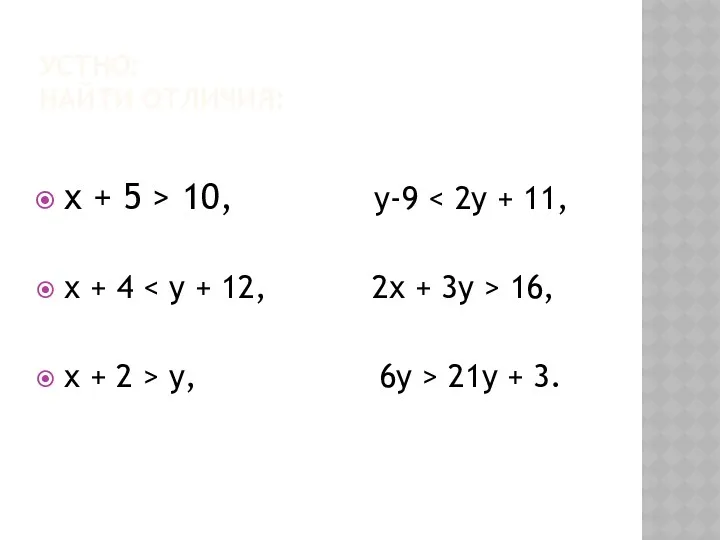 Решение неравенств с двумя переменными
Решение неравенств с двумя переменными Решение прикладных задач с использованием основных свойств вероятности
Решение прикладных задач с использованием основных свойств вероятности Вычитание из чисел 6 и 7. Состав чисел 6 и 7
Вычитание из чисел 6 и 7. Состав чисел 6 и 7 конкурс по математике Эврика
конкурс по математике Эврика Десятичные дроби. Округление чисел
Десятичные дроби. Округление чисел Устный счёт Сложение трёхзначных чисел Диск
Устный счёт Сложение трёхзначных чисел Диск Увеличить, уменьшить в несколько раз урок математики для 3 класса по программе Гармония
Увеличить, уменьшить в несколько раз урок математики для 3 класса по программе Гармония Сумма углов треугольника
Сумма углов треугольника Математика. 5 класс. Найди правильный ответ:
Математика. 5 класс. Найди правильный ответ: Решение треугольников. 9 класс
Решение треугольников. 9 класс Метод наименьших квадратов
Метод наименьших квадратов Презентация к уроку математики во 2классе.
Презентация к уроку математики во 2классе. Функции. Их свойства и графики
Функции. Их свойства и графики Лекция 6 по статистике. Изучение вариации
Лекция 6 по статистике. Изучение вариации Четырехугольники
Четырехугольники