Содержание
- 2. Истинная модель парной линейной регрессии Y = а + b*X + e. Для ее оценки используется
- 3. Для элемента (Yi, Xi) выборки, i = 1, …, n, можно записать:
- 4. Как оцениваются по выборке коэффициенты регрессии?
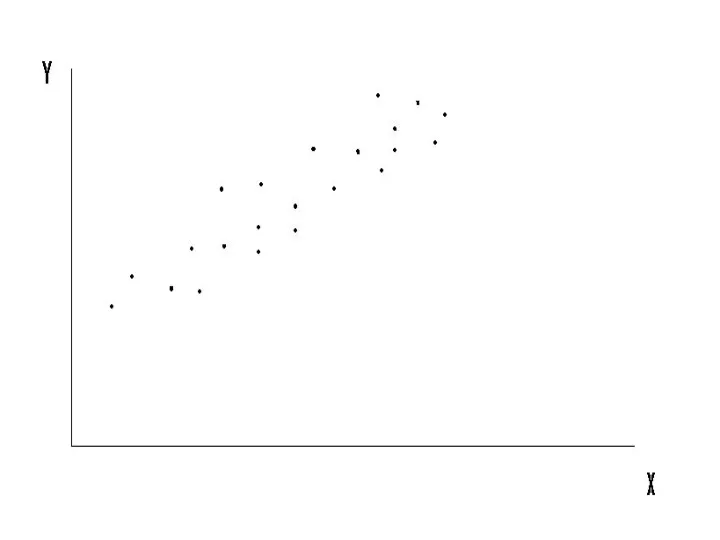
- 5. Выборка (Yi, Xi), по которой мы должны оценить теоретическую модель Y = a + b*X +
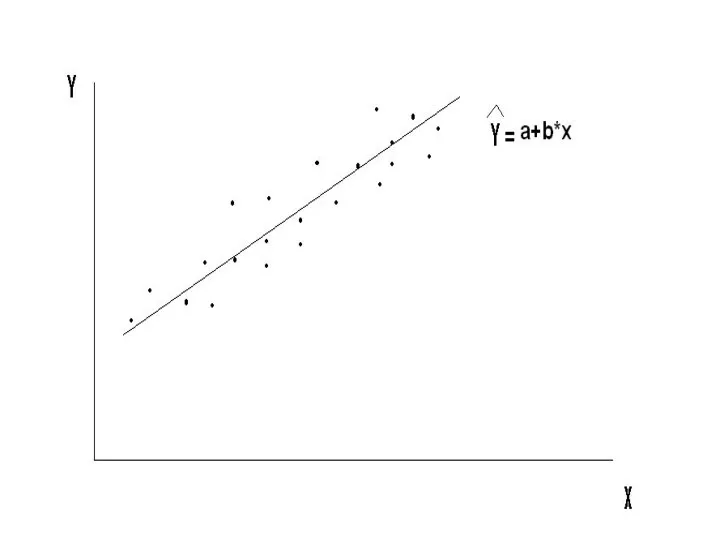
- 7. По этим точкам мы хотим получить такое выборочное уравнение (т. е. оценки a и b), которое
- 8. Интуиция подсказывает: Чем лучше оцененная прямая регрессии представляет выборку, тем точнее она приближает истинную прямую регрессии.
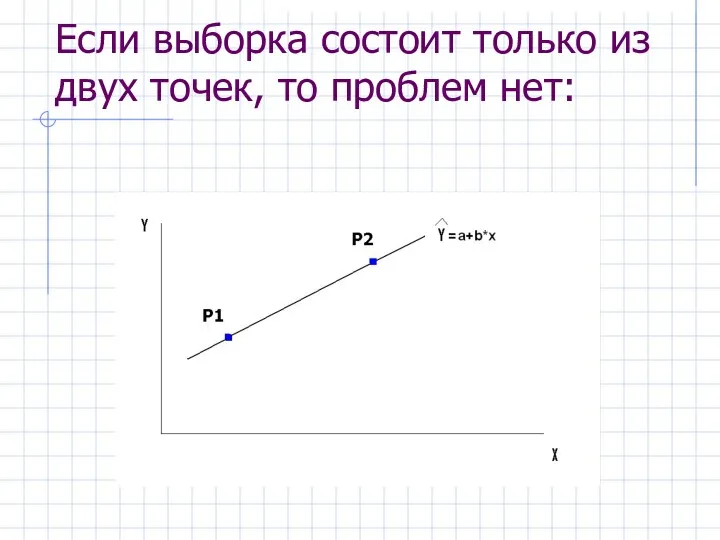
- 10. Если выборка состоит только из двух точек, то проблем нет:
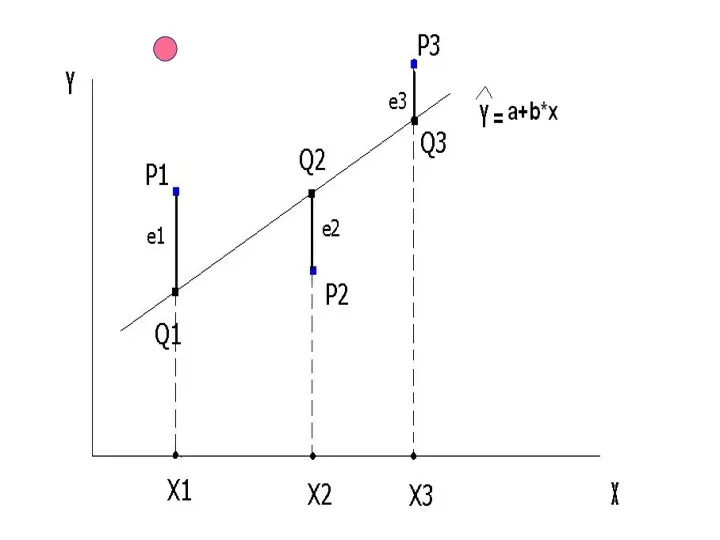
- 11. Если точек больше двух:
- 13. Точки выборки P1 = (X1, Y1), P2 = (X2, Y2), P3 = (X3, Y3) моделируются (оцениваются)
- 14. Принцип метода наименьших квадратов Для данной выборки (X1, Y1), …, (Xn, Yn) параметры a и b
- 15. Или
- 16. Решаем систему уравнений:
- 17. После преобразований получаем систему нормальных уравнений для коэффициентов регрессии
- 18. Решение этой системы дает значения для оценок параметров уравнения регрессии a и b:
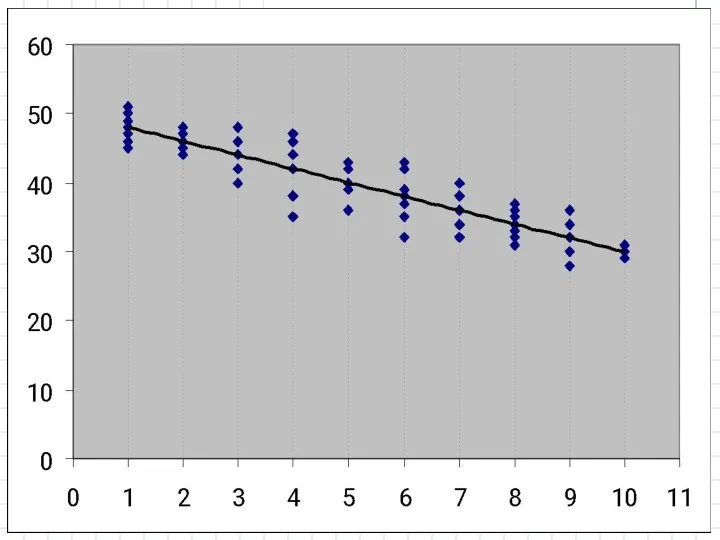
- 19. Решение уравнения регрессии в Excel На листе Excel выделяют блок ячеек в котором - строк всегда
- 20. Решение уравнения регрессии в Excel 3. В выделенном блоке ячеек будет результат в виде значения параметров
- 21. Коэффициент детерминации показывает, насколько хорошо в выборке изменения Y объяснены изменениями Х. Т. е., насколько хорошо
- 22. Коэффициент детерминации: - часть дисперсии Y, объясненная уравнением регрессии, т. е. изменениями в выборке фактора Х.
- 23. Еще одно дополнение к R2 Мы знаем, что 0 ≤ R2 ≤ 1. Однако, если модель
- 24. Статистические свойства МНК-оценок коэффициентов регрессии. ТЕОРЕМА ГАУССА-МАРКОВА
- 25. Почему при оценке параметров модели a и b минимизируется именно ? Потому что при выполнении некоторых
- 26. Каких условий? МНК-оценки a и b являются случайными величинами, свойства которых существенным образом зависят от свойств
- 27. Условия Гаусса-Маркова 1. Математическое ожиданиет значений остатков e равно 0: М(ei) = 0 для всех наблюдений
- 28. Для уравнения множественной регрессии: 6. Факторы xi независимы между собой в том смысле, что их выборочные
- 29. Модель, удовлетворяющая предпосылкам МНК (1)-(7), называется классической нормальной моделью регрессии, если не выполняется только условие (7),
- 31. Если 1-е условие Г-М не выполняется, МНК дает смещенную оценку для b.
- 32. 2. σei2 = σ2 = const для всех наблюдений Xi Условие гомоскедастичности ошибок. Когда оно не
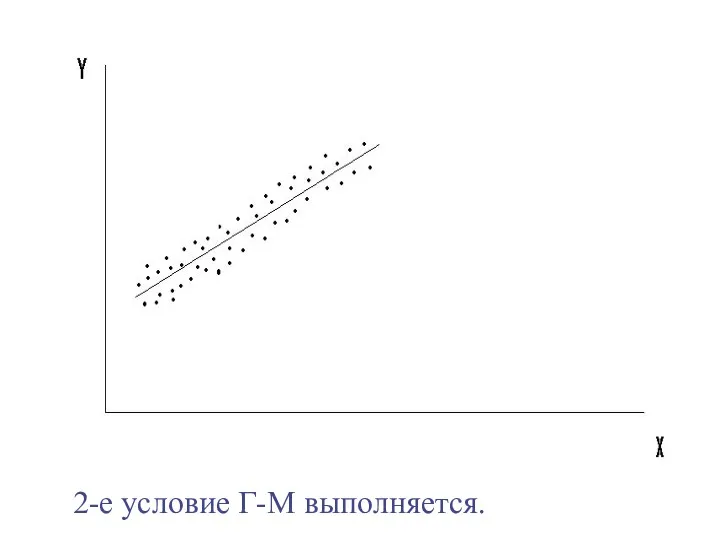
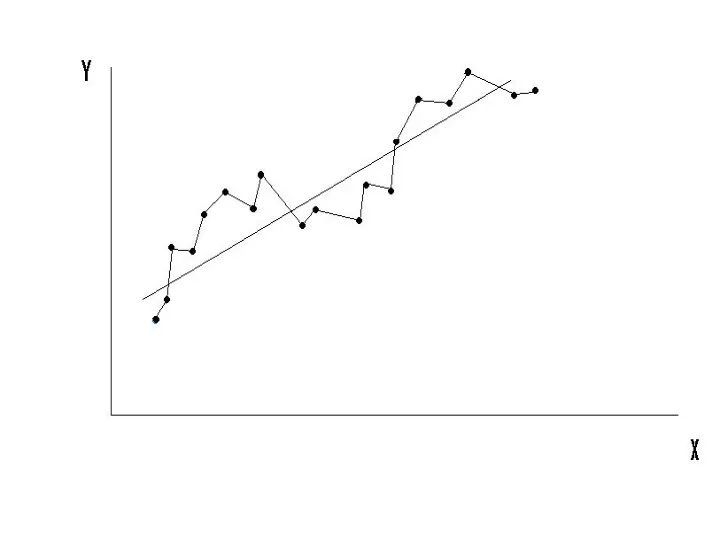
- 33. 2-е условие Г-М выполняется.
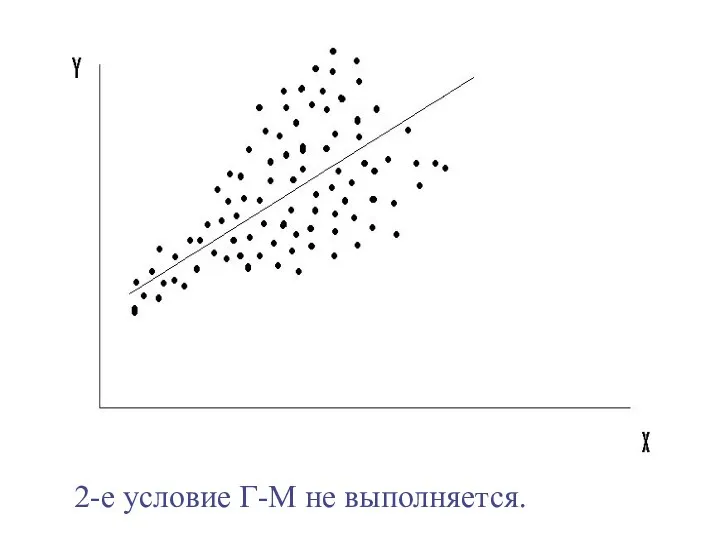
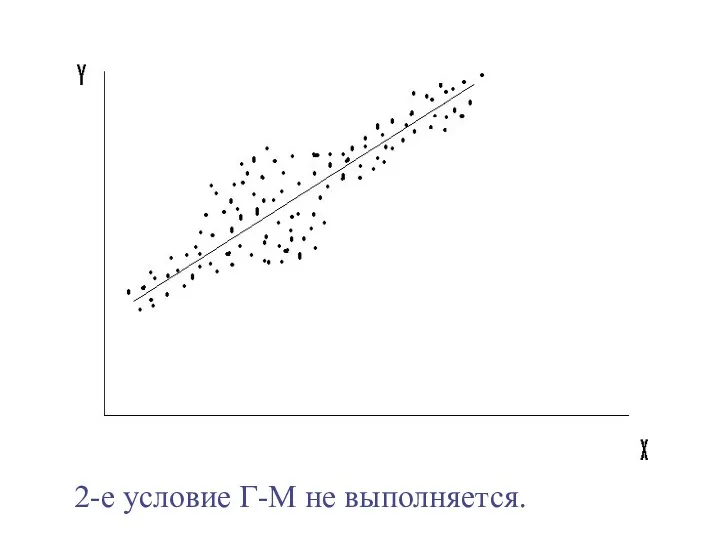
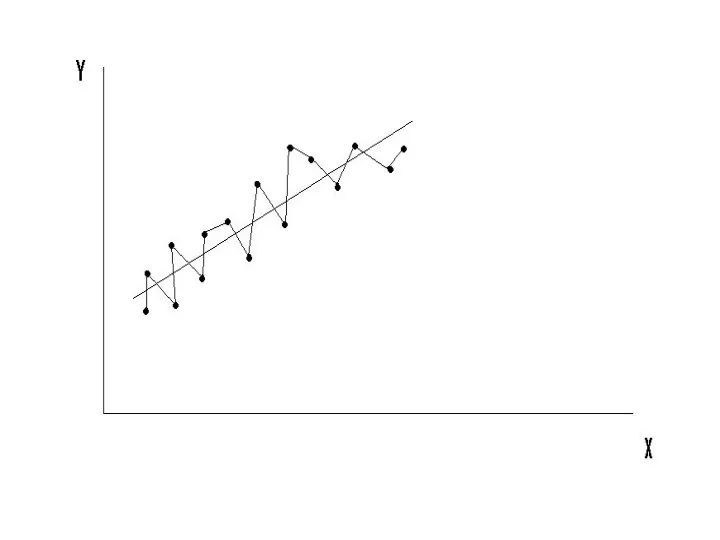
- 34. 2-е условие Г-М не выполняется.
- 35. 2-е условие Г-М не выполняется.
- 36. 3. σei, ej = 0 для всех Xi и Xj, i ≠ j . Условие некоррелированности
- 39. 4. σXi, ei = 0 для всех наблюдений. Случайный член распределен независимо от объясняющей переменной. Это
- 40. Дополнительное условие: 7. Случайный член, i=1, …, n, имеет нормальное распределение, ei ~ N(0, σe2)
- 41. Это условие не нужно для обеспечения хороших свойств оценок a и b. Но оно позволяет корректно
- 42. Теорема Гаусса-Маркова Если предпосылки МНК соблюдаются, то оценки, полученные по МНК, обладают следующими свойствами: Оценки параметров
- 43. F-критерий Фишера Если Fрасч ≥ Fтабл , то отвергается гипотеза H0 и признается значимость и надежность
- 44. t-статистика Стьюдента H0 – гипотеза о статистической незначимости оценок параметров уравнения регрессии и показателя тесноты связи:
- 45. Формулы для расчета случайных ошибок: ^ ^
- 46. Расчет доверительного интервала прогноза где Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна,
- 48. Скачать презентацию









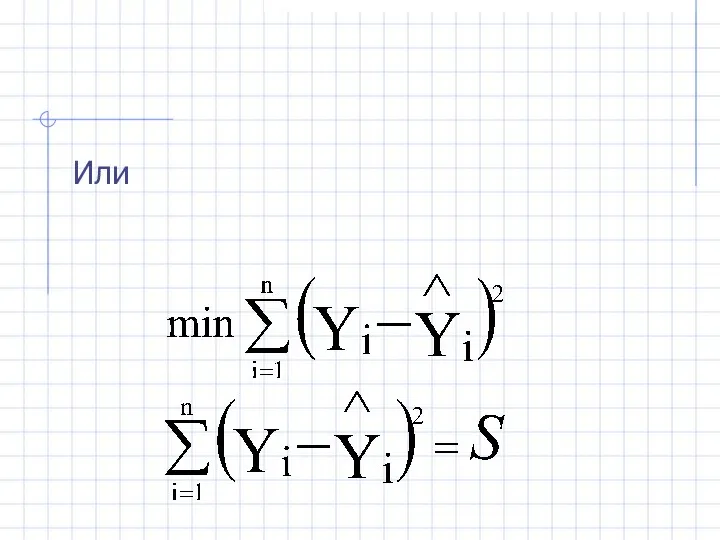

























 Презентация по математике. Тема Сложение однозначных чисел с переходом через десяток вида ...+8, ....+9
Презентация по математике. Тема Сложение однозначных чисел с переходом через десяток вида ...+8, ....+9 Упрощение выражений, задачи на части, порядок действий
Упрощение выражений, задачи на части, порядок действий 20230607_prezentatsiya_po_matematike_kvadrat_summy_
20230607_prezentatsiya_po_matematike_kvadrat_summy_ Фінансова математика. Тема: Прості та складні відсотки
Фінансова математика. Тема: Прості та складні відсотки Числовые последовательности
Числовые последовательности Правильные и неправильные дроби
Правильные и неправильные дроби Решение задач. Закрепление.
Решение задач. Закрепление. Предел числовой последовательности
Предел числовой последовательности Прямоугольный параллелепипед
Прямоугольный параллелепипед Презентация для 2 класса. Игры Щифровальщик, Палиндромы (занимательная математика)
Презентация для 2 класса. Игры Щифровальщик, Палиндромы (занимательная математика) Отказы и их причины. Статистический анализ
Отказы и их причины. Статистический анализ Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Логические задачи (геометрия 1 класс)
Логические задачи (геометрия 1 класс) Правильные и неправильные дроби
Правильные и неправильные дроби Числовые и алгебраические выражения
Числовые и алгебраические выражения Запись линейных алгоритмов в графическом представлении. (урок 3)
Запись линейных алгоритмов в графическом представлении. (урок 3) Трёхмерное пространство. Координатная плоскость
Трёхмерное пространство. Координатная плоскость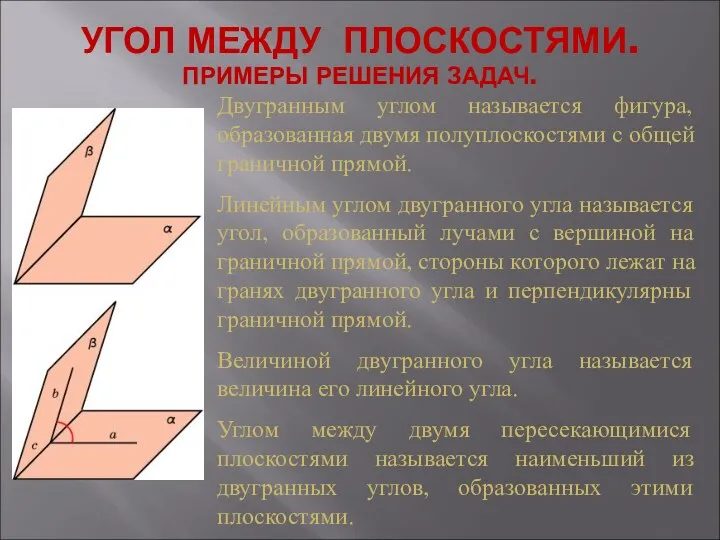 Угол между плоскостями. Примеры решения задач
Угол между плоскостями. Примеры решения задач Элементы Комбинаторики Множество и операции над ними
Элементы Комбинаторики Множество и операции над ними Задачи линейного программирования
Задачи линейного программирования Задачи по теории вероятностей
Задачи по теории вероятностей натуральный ряд
натуральный ряд Сходимость знакопеременных рядов
Сходимость знакопеременных рядов Задание №15 базового уровня. Равнобедренный треугольник: вычисление углов
Задание №15 базового уровня. Равнобедренный треугольник: вычисление углов Economics of pricing and decision making. (Lecture 1)
Economics of pricing and decision making. (Lecture 1) Перпендикулярные прямые
Перпендикулярные прямые Задачи на построение сечений тетраэдра и параллелепипеда
Задачи на построение сечений тетраэдра и параллелепипеда Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем