Содержание
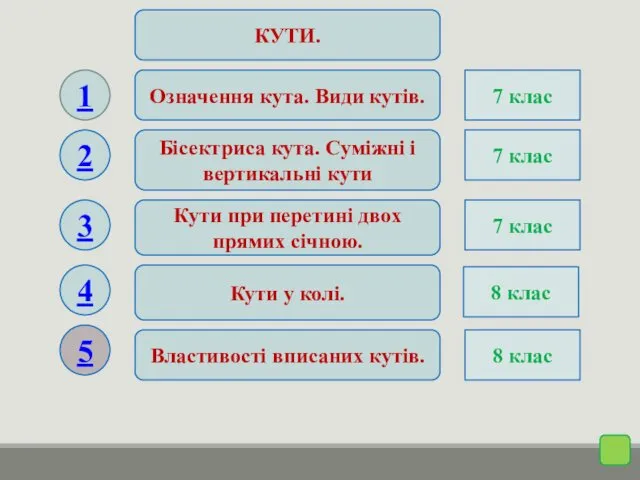
- 2. Означення кута. Види кутів. Бісектриса кута. Суміжні і вертикальні кути Кути при перетині двох прямих січною.
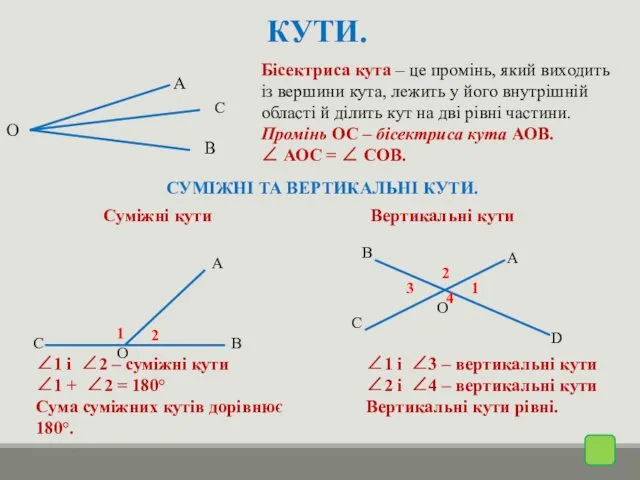
- 3. КУТИ. А В С О Бісектриса кута – це промінь, який виходить із вершини кута, лежить
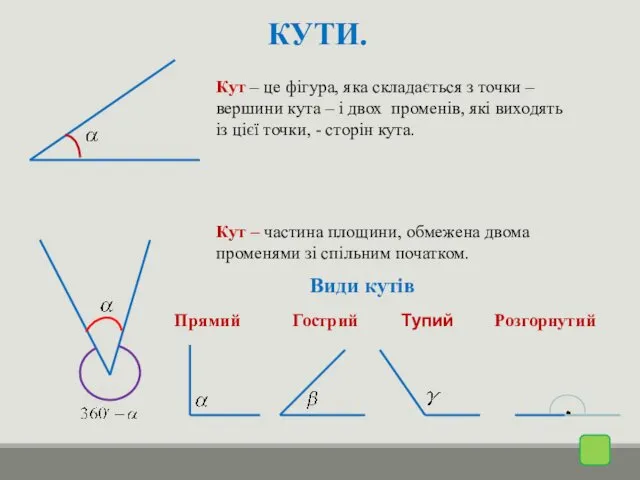
- 4. КУТИ. Кут – це фігура, яка складається з точки – вершини кута – і двох променів,
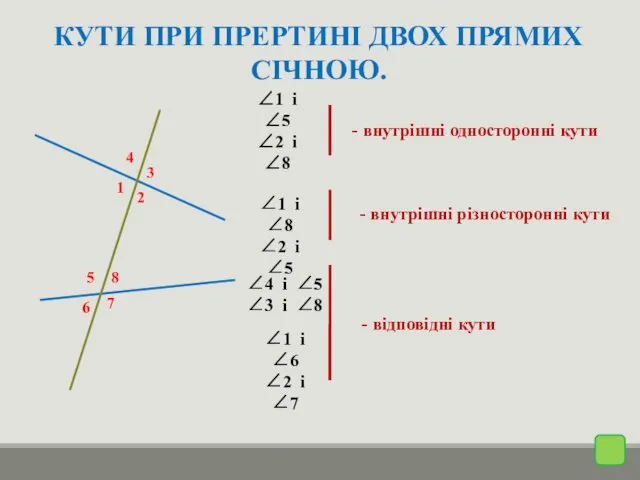
- 5. КУТИ ПРИ ПРЕРТИНІ ДВОХ ПРЯМИХ СІЧНОЮ. 1 4 3 2 8 5 7 6 ∠1 і
- 6. КУТИ У КОЛІ. Центральний кут Вписаний кут А О В А В О О В А
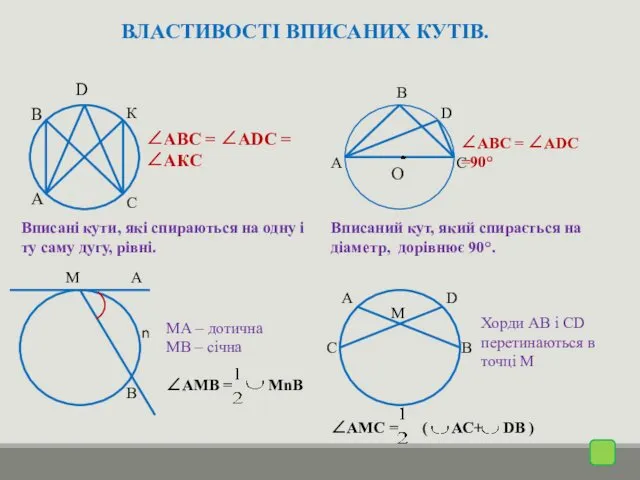
- 7. ВЛАСТИВОСТІ ВПИСАНИХ КУТІВ. D А В С К ∠АВС = ∠АDC = ∠АКС А В С
- 8. ТРИКУТНИКИ Рівність трикутників Властивості трикутника Висота, медіана, бісектриса та середня лінія трикутника. Рівнобедрений трикутник Властивості рівнобедреного
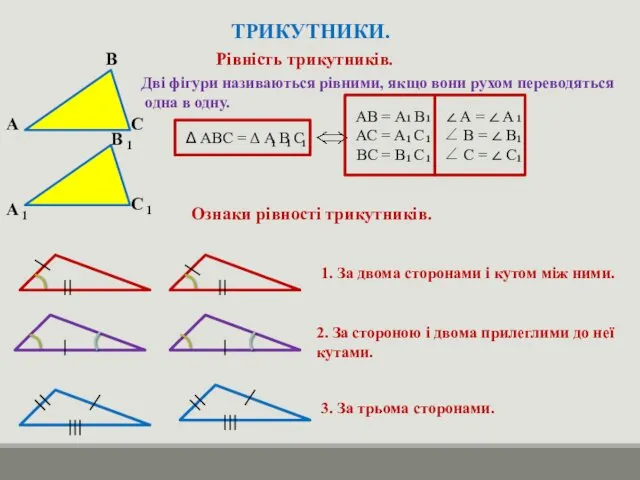
- 9. ТРИКУТНИКИ. Рівність трикутників. А В С А В С 1 1 1 Дві фігури називаються рівними,
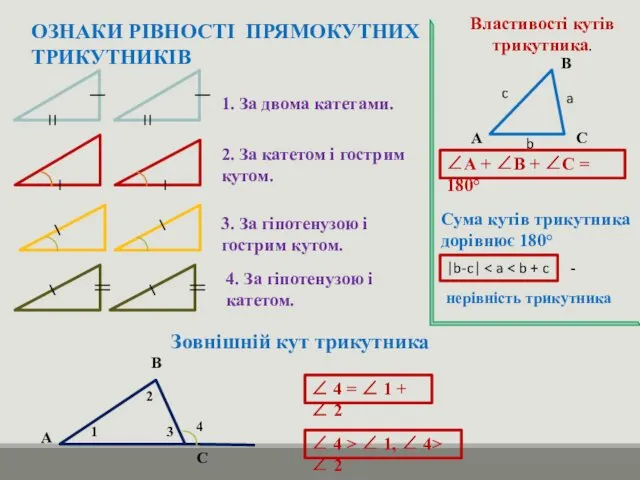
- 10. ОЗНАКИ РІВНОСТІ ПРЯМОКУТНИХ ТРИКУТНИКІВ 1. За двома катетами. 2. За катетом і гострим кутом. 3. За
- 11. РІВНОБЕДРЕНИЙ ТРИКУТНИК. А В С А В С D Трикутник називається рівнобедреним, якщо у нього дві
- 12. РІВНОБЕДРЕНИЙ ТРИКУТНИК. А В С D Властивості Якщо в Δ АВС АВ = ВС, то ∠
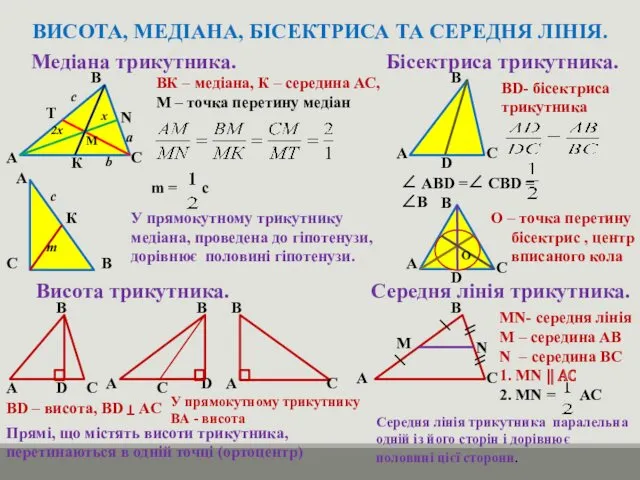
- 13. ВИСОТА, МЕДІАНА, БІСЕКТРИСА ТА СЕРЕДНЯ ЛІНІЯ. Медіана трикутника. А В С М Т К N x
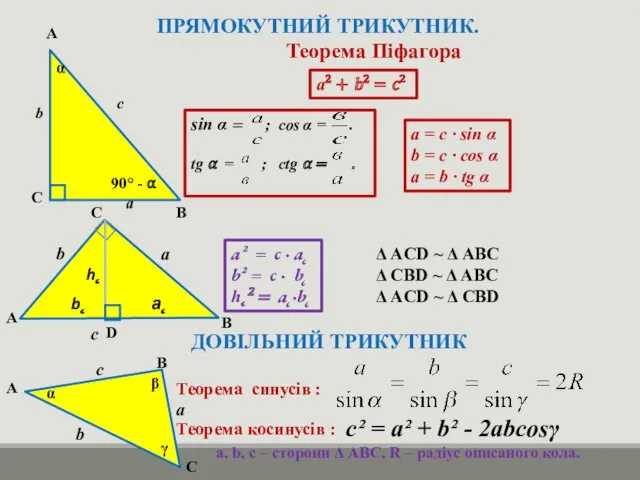
- 14. ПРЯМОКУТНИЙ ТРИКУТНИК. Теорема Піфагора a² + b² = c² sin α = ; cos α =
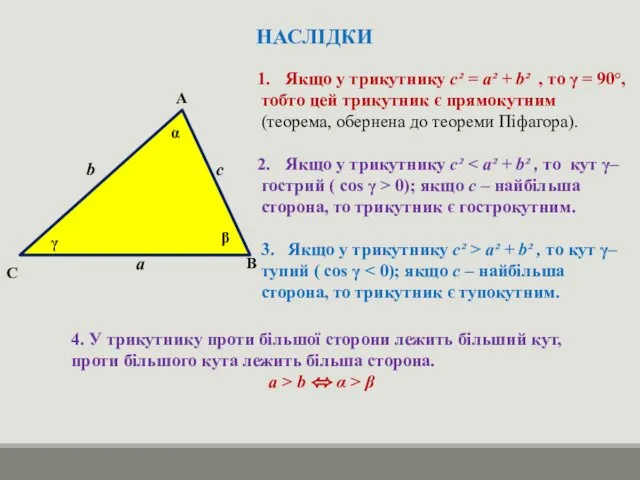
- 15. НАСЛІДКИ А В С α β γ а b с Якщо у трикутнику с² = а²
- 16. ПЛОЩА ТРИКУТНИКА Довільний трикутник S = a ∙ h S = a∙ b∙ sinγ S =
- 18. Скачать презентацию





 Определенный интеграл
Определенный интеграл Математика
Математика С Бибигоном на Луну
С Бибигоном на Луну Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Признаки равенства треугольников. Равнобедренный треугольник. Тест
Признаки равенства треугольников. Равнобедренный треугольник. Тест Презентация к уроку математики во 2 классе Умножение и деление на 3. Третья часть числа
Презентация к уроку математики во 2 классе Умножение и деление на 3. Третья часть числа Дисперсионный анализ
Дисперсионный анализ Математическая игра Магия чисел
Математическая игра Магия чисел ЕГЭ. Задачи на смеси и сплавы
ЕГЭ. Задачи на смеси и сплавы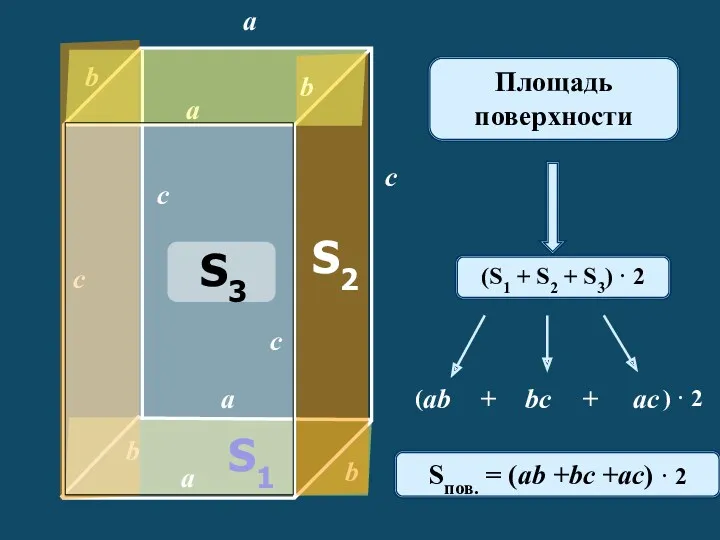 Площадь поверхности
Площадь поверхности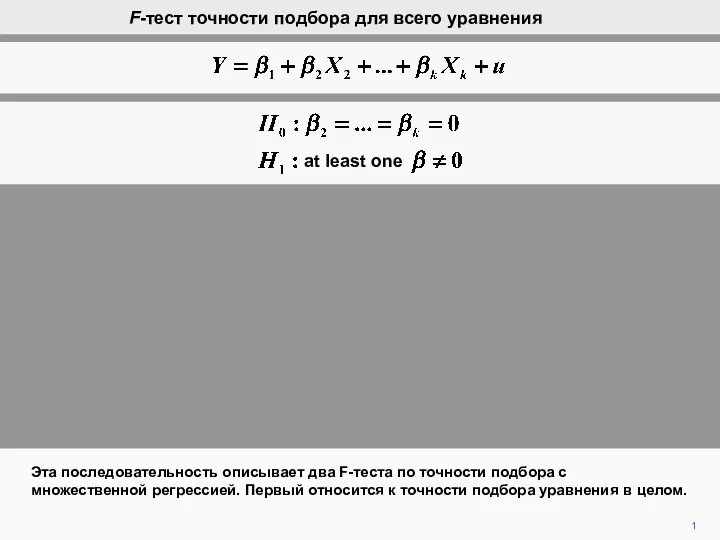 F-тест точности подбора для всего уравнения
F-тест точности подбора для всего уравнения Наибольший общий делитель. Взаимно простые числа
Наибольший общий делитель. Взаимно простые числа Уравнение. 5 класс
Уравнение. 5 класс Способ группировки
Способ группировки Расстояние от точки до прямой. Расстояние между параллельными прямыми
Расстояние от точки до прямой. Расстояние между параллельными прямыми Признаки равенства треугольников. Задачи на готовых чертежах
Признаки равенства треугольников. Задачи на готовых чертежах Решение задач 4класс УМК Гармония
Решение задач 4класс УМК Гармония Двусвязность. (Лекция 7)
Двусвязность. (Лекция 7) Дроби. Происхождение дробей
Дроби. Происхождение дробей Теория Вероятностей
Теория Вероятностей Великие математики
Великие математики Осевая и центральная симметрия
Осевая и центральная симметрия Научный проект по математике
Научный проект по математике Конкурс смекалки
Конкурс смекалки План построения графика функции с помощью производной
План построения графика функции с помощью производной Интегрирование иррациональных функций
Интегрирование иррациональных функций Презентация Час. Минута
Презентация Час. Минута