Слайд 2

При этом первые два интеграла приводятся к табличным, а третий –
к сумме двух табличных интегралов.
Пример№1. Найти интеграл:
Решение: Так как
Слайд 3

Пример №2.Найти интеграл :
Решение: Выделим полный квадрат :
Сделаем подстановку:
Тогда:
Слайд 4

Интегрирование тригонометрических функций
Интегралы вида
Находятся с помощью формул:
Слайд 5

Пример №1. Найти интеграл:
Решение:Воспользуемся формулой
Получим:
Тогда
Слайд 6

Пример№2. Найти интеграл:
Решение: Воспользуемся формулой:
Получим:
Тогда
Слайд 7

Пример№3. Найти интеграл:
Решение: Воспользуемся формулой:
Получим:
Тогда:
Слайд 8

Интегралы типа
Для нахождения таких интегралов используются следующие приемы:
Подстановка если целое
положительное нечетное число;
Подстановка если целое положительное нечетное число;
Формулы понижения порядка:
Если целые неотрицательные четные числа;
4)Подстановка если есть четное отрицательное целое число.
Слайд 9

Пример№1. Найти интеграл:
Решение: Применим подстановку Т.к.n=5 (1 cлучай).
Тогда
Получим:
Слайд 10
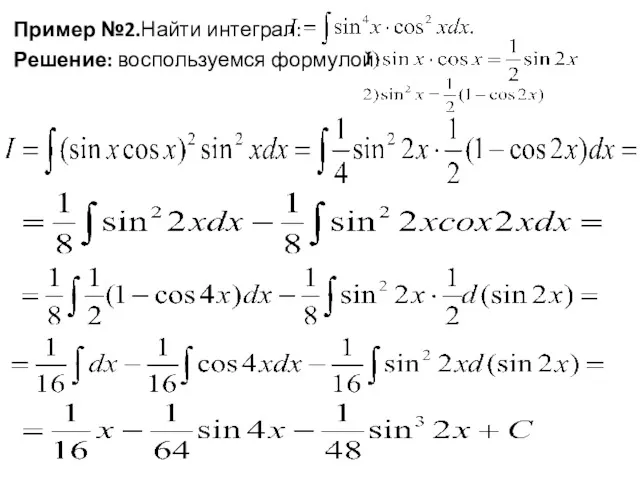
Пример №2.Найти интеграл:
Решение: воспользуемся формулой:
Слайд 11

Пример №3. Найти интеграл:
Решение:Здесь (4 случай)
Обозначим Тогда
Получим:
Слайд 12

Универсальная тригонометрическая подстановка
Рассмотрим некоторые случаи нахождения интеграла от тригонометрическихфункций.Функцию с переменными
и ,над которыми выполняются рациональные действия (сложения,вычитание,умножение иделение)
Принято обозначать знак рациональной функции.
Вычисление неопределённых интегралов типа
Сводится к вычислению интегралов от рациональной функции подстановкой ,которая называется универсальной
Слайд 13

Действительно,
Поэтому
Где рациональная функция от .Обычно этот способ весьма громоздкий,зато всегда приводит
к результату.
Слайд 14

На практике применяют и другие,более простые подстановки,
в зависимости от свойств (
и вида) подынтегральной функции.В частности,удобны следующие правила:
1)Если функция нечётна относительно
Т.е ,то подстановка
рационализирует интеграл;
2)Если функция нечётна относительно
Т.е. ,то делается подстановка
3)Если функция четна относительно
,то интеграл рационализируется подстановкой .Такая же подстановка применяется,если интеграл имеет вид








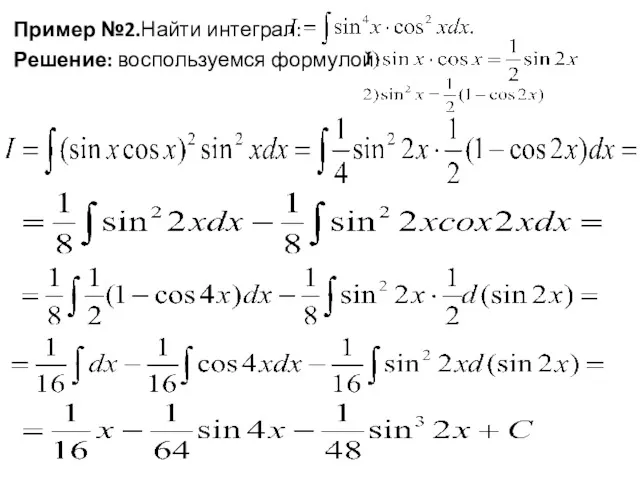




 Многоугольники
Многоугольники Относительная частота и закон больших чисел (9 класс)
Относительная частота и закон больших чисел (9 класс) Confidence interval estimation
Confidence interval estimation Поняття похідної функції. Основні правила диференціювання. Таблиця похідних
Поняття похідної функції. Основні правила диференціювання. Таблиця похідних Использование ИКТ
Использование ИКТ Похідна. Правила диференціювання
Похідна. Правила диференціювання Рациональные числа
Рациональные числа Предмет эконометрики. Основные эконометрические модели
Предмет эконометрики. Основные эконометрические модели Площади многоугольников
Площади многоугольников Устный счет. 1 класс
Устный счет. 1 класс Решение занимательных задач
Решение занимательных задач Многоугольники. Равные фигуры
Многоугольники. Равные фигуры Зеленая аптека Кузбасса. Проценты
Зеленая аптека Кузбасса. Проценты Прямоугольный параллелепипед
Прямоугольный параллелепипед Решаем задачи на умножение и деление
Решаем задачи на умножение и деление Градиентные и генетические методы решения оптимизационных задач
Градиентные и генетические методы решения оптимизационных задач Урок математики в 1 классе Повторение и закрепление пройденного материала о величинах.
Урок математики в 1 классе Повторение и закрепление пройденного материала о величинах. Методы непараметрического спектрального анализа. Метод периодограмм Уэлча
Методы непараметрического спектрального анализа. Метод периодограмм Уэлча Биссектриса угла
Биссектриса угла Correlation Analysis and Covariance
Correlation Analysis and Covariance Решение задач на движение (навстречу и вдогонку)
Решение задач на движение (навстречу и вдогонку) Решение дифференциальных уравнений. (Лекция 6)
Решение дифференциальных уравнений. (Лекция 6) Матрицы, операции над матрицами, теорема существования обратной матрицы. Матричная запись систем линейных уравнений
Матрицы, операции над матрицами, теорема существования обратной матрицы. Матричная запись систем линейных уравнений Конус. Усеченный конус. Решение задач
Конус. Усеченный конус. Решение задач Старинная ярмарка
Старинная ярмарка Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Примеры на вычитание с переходом через десяток в пределах 20. 1 класс
Примеры на вычитание с переходом через десяток в пределах 20. 1 класс