Содержание
- 2. 1. Теорема сложения вероятностей несовместимых событий Теорема. Вероятность суммы двух несовместимых событий А и В равна
- 3. 1. Теорема сложения вероятностей несовместимых событий Следствие 1. Если события А1, А2, ..., Аn образуют полную
- 4. 1. Теорема сложения вероятностей несовместимых событий Следствие 2. Сумма вероятностей противоположных событий А и Ā равна
- 5. 2. Теорема умножения вероятностей Определение 1. Два события А и В называют независимыми, если вероятность появления
- 6. Предположим теперь, что вынутый шар в первом испытании не кладется обратно в урну. Тогда, если произошло
- 7. Определение 2. Пусть А и В - зависимые события. Условной вероятностью РА(В) события В называют вероятность
- 8. Теорема 1. Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них
- 9. Применив формулу (7) к событию ВА, получим Р(ВА) = Р(В)РВ(А). (7') Так как АВ = ВА,
- 10. Задача. В группе туристов 20% детей, причем 12% девочки. Наугад выбирают ребенка. Какова вероятность того, что
- 11. Задача. Предположим, что вероятности встретить реку, загрязняемую постоянным фактором А – Р(А), временным фактором В –
- 12. Теорема 2. Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий Р(АВ)
- 13. Замечание 1. Если события А1, А2, ..., Аn независимы в совокупности, то и противоположные им события
- 14. Теорема 3. Если события А1, А2, ..., Аn независимы в совокупности, то вероятность наступления хотя бы
- 15. Теорема. Вероятность суммы двух совместимых событий А и В равна сумме вероятностей этих событий минус вероятность
- 16. Замечание 1. При использовании формулы (13) следует иметь в виду, что события А и В могут
- 17. Пример. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: Р(А) = 0,7
- 18. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из п попарно несовместимых
- 19. Задача. В санатории 30% пациентов - мужчины (М) и 70% - женщины (Ж). Болезни сердца среди
- 20. Пусть в условиях рассуждения, относящегося к формуле полной вероятности, осуществлено одно испытание, в результате которого произошло
- 21. Формулы Байеса применяются, когда событие А, которое может появиться только с одной из гипотез В1, В2,
- 23. Скачать презентацию




















 Графическая интерпретация ЗЛП
Графическая интерпретация ЗЛП Сложение и вычитание чисел
Сложение и вычитание чисел Арифметическая прогрессия
Арифметическая прогрессия Решение неравенств второй степени с двумя переменными
Решение неравенств второй степени с двумя переменными Как называются числа при вычитании
Как называются числа при вычитании Информационные модели. Использование графов для решения задач
Информационные модели. Использование графов для решения задач Математика, как наука
Математика, как наука Площадь плоских фигур
Площадь плоских фигур Состав чисел в пределах 10. Закрепление
Состав чисел в пределах 10. Закрепление Второй и третий признаки равенства треугольников. Урок 1
Второй и третий признаки равенства треугольников. Урок 1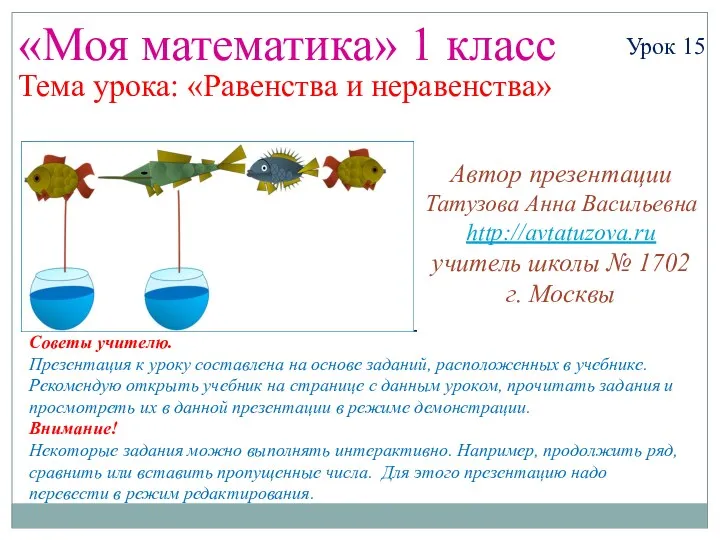 Математика. 1 класс. Урок 15. Равенства и неравенства. Презентация
Математика. 1 класс. Урок 15. Равенства и неравенства. Презентация Занимательная геометрия для старших дошкольников
Занимательная геометрия для старших дошкольников Основные формулы к задачам типа В9
Основные формулы к задачам типа В9 Формула стоимости
Формула стоимости Разложение многочлена на множители
Разложение многочлена на множители Наибольший общий делитель. Взаимно простые числа. 6 класс
Наибольший общий делитель. Взаимно простые числа. 6 класс Как люди научились счиать
Как люди научились счиать Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость. Задания
Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость. Задания Знакомство с новой единицей измерения длины. Дециметр
Знакомство с новой единицей измерения длины. Дециметр Степень с рациональным показателем
Степень с рациональным показателем Прибавить и вычесть 1.Веселое путешествие
Прибавить и вычесть 1.Веселое путешествие Класифікація кутів
Класифікація кутів Презентация Путешествие в страну дробей
Презентация Путешествие в страну дробей Тригонометрические уравнения
Тригонометрические уравнения Матриці, дії з матрицями. Визначники, їх властивості
Матриці, дії з матрицями. Визначники, їх властивості Метод наименьших квадратов
Метод наименьших квадратов Дидактические игры по формированию элементарных математических представлений детей от 3 до 4 лет.
Дидактические игры по формированию элементарных математических представлений детей от 3 до 4 лет. Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2
Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2