Содержание
- 2. ЛОГИКА ВЫСКАЗЫВАНИЙ Логика высказываний (ЛВ) – общее название для класса логических систем (точнее, теорий), выразительные средства
- 3. КЛАССИЧЕСКАЯ ЛОГИКА ВЫСКАЗЫВАНИЙ Теория типа «Логика высказываний» будет классической, если она основывается на принципах * двузначности
- 4. СЛОЖНЫЕ И ПРОСТЫЕ ВЫСКАЗЫВАНИЯ Сложные высказывания – такие высказывания, в составе которых можно выделить другие высказывания
- 5. СЛОЖНЫЕ И ПРОСТЫЕ ВЫСКАЗЫВАНИЯ Сложные высказывания – такие высказывания, в составе которых можно выделить другие высказывания
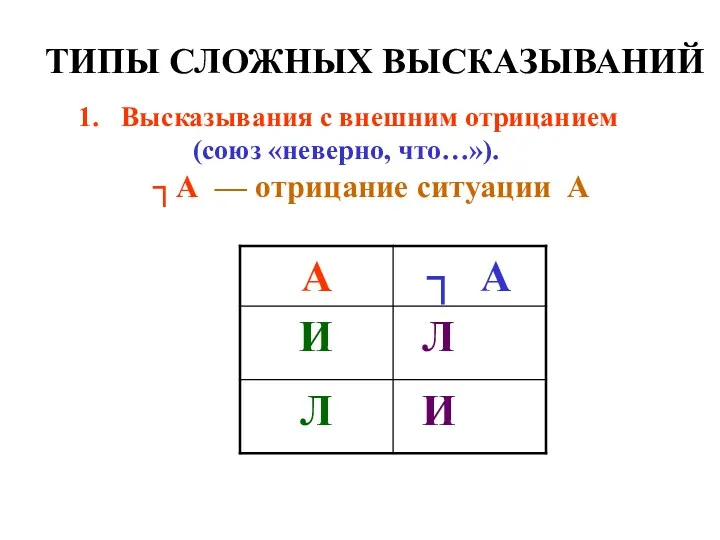
- 6. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ Высказывания с внешним отрицанием (союз «неверно, что…»). ┐А — отрицание ситуации А
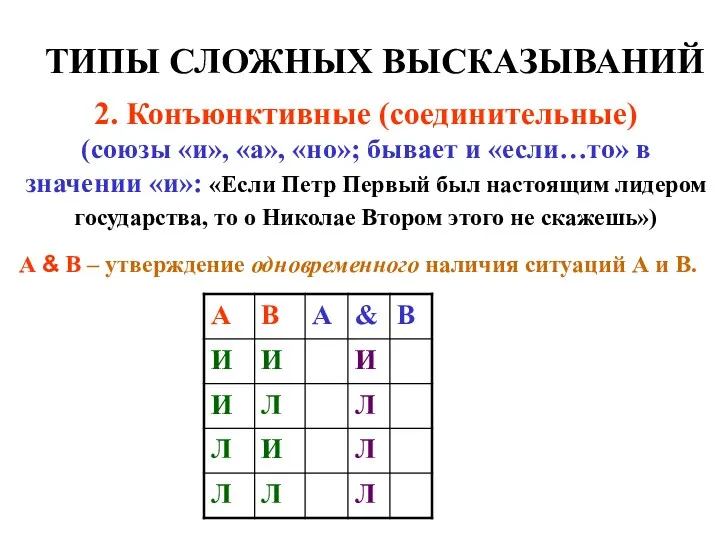
- 7. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 2. Конъюнктивные (соединительные) (союзы «и», «а», «но»; бывает и «если…то» в значении «и»:
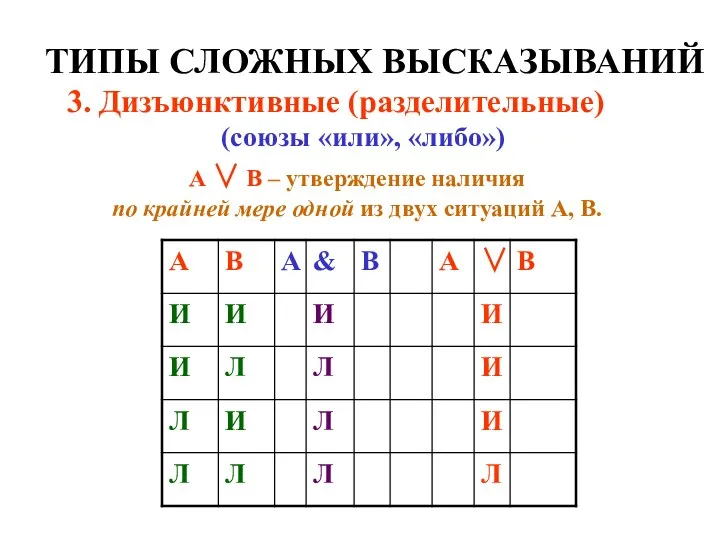
- 8. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 3. Дизъюнктивные (разделительные) (союзы «или», «либо») А ∨ В – утверждение наличия по
- 9. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 4. Строго дизъюнктивные (союзы «или…или…», «либо…либо…») А ∨ В – утверждение наличия ровно
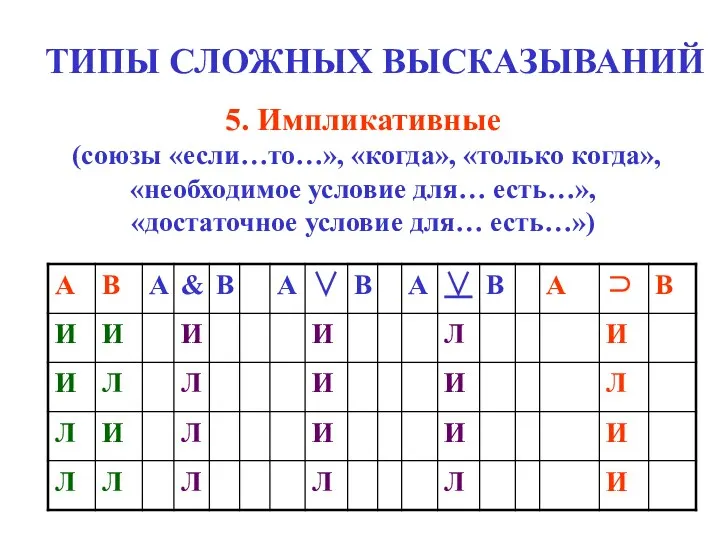
- 10. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 5. Импликативные (союзы «если…то…», «когда», «только когда», «необходимое условие для… есть…», «достаточное условие
- 11. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 5. Импликативные (союзы «если…то…», «когда», «только когда», «необходимое условие для… есть…», «достаточное условие
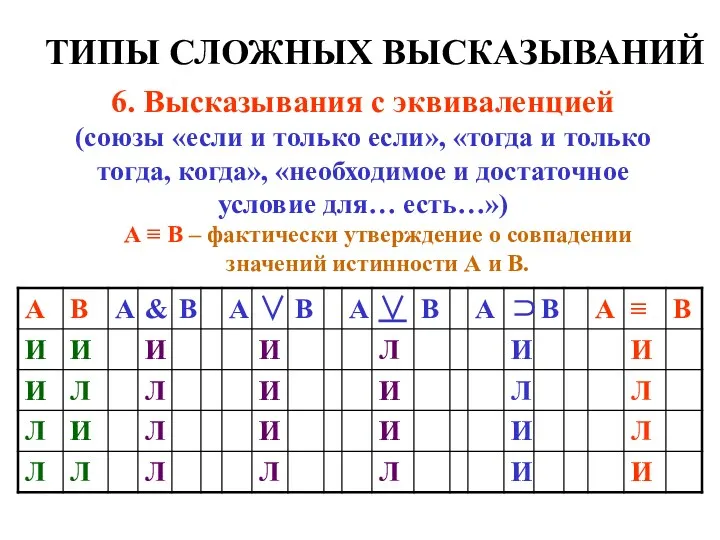
- 12. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 6. Высказывания с эквиваленцией (союзы «если и только если», «тогда и только тогда,
- 13. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 7. Высказывания с функтором Нико (союз «ни…ни…») А ↓ В – утверждение об
- 14. ТИПЫ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ 8. Высказывания с функтором Шеффера (союз «или не…или не… или и то, и
- 15. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 16. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 17. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 18. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 19. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 20. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 21. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 22. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 23. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 24. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 25. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 26. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 27. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 28. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 29. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 30. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 31. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 32. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 33. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 34. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 35. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 36. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 37. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 38. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 39. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 40. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 41. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 42. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 43. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 44. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 45. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 46. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 47. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 48. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 49. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 50. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
- 51. Вычисление значения сложной формулы (┐ (p ⏐ q) ⊃ (┐ p ≡ q)) & ┐ ((┐
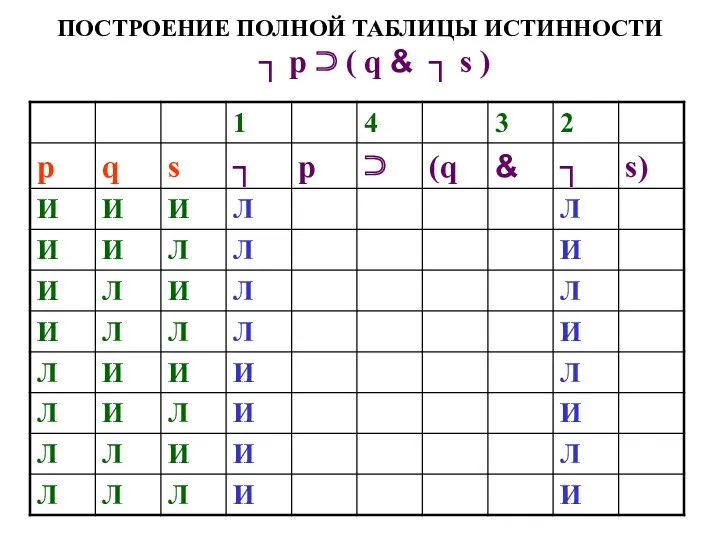
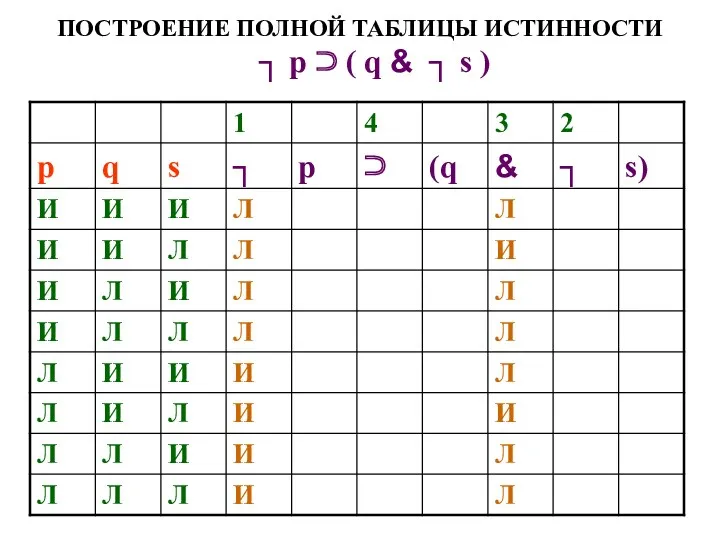
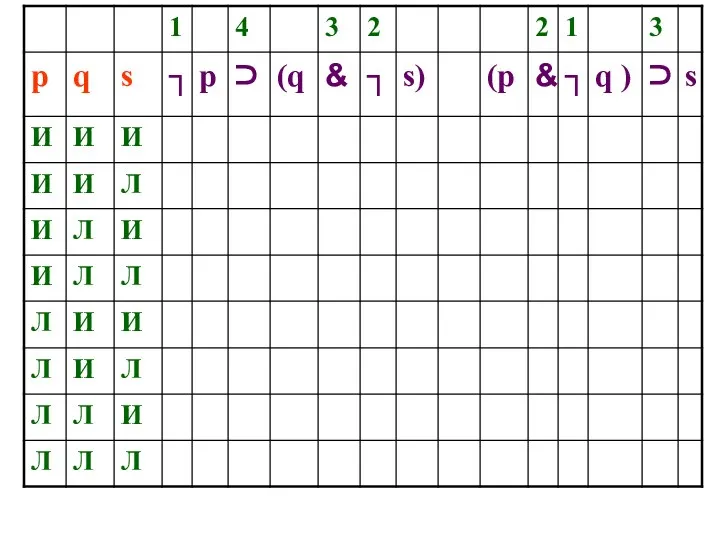
- 52. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ Построим полную таблицу истинности (для всех возможных положений вещей) для высказывания Если
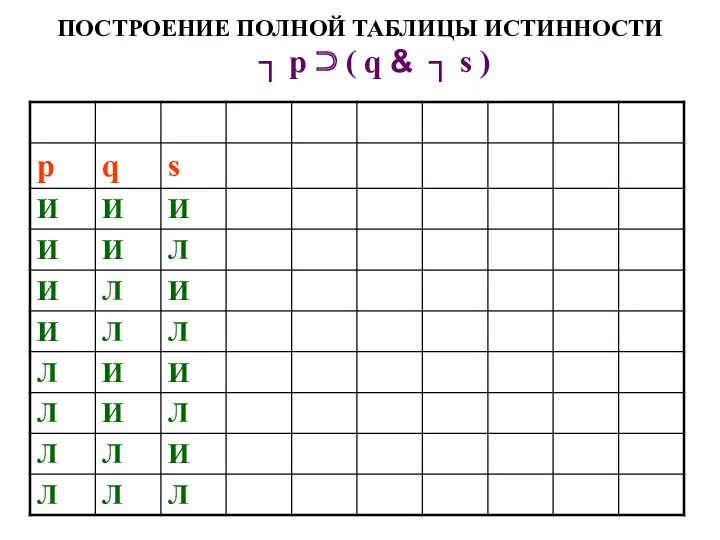
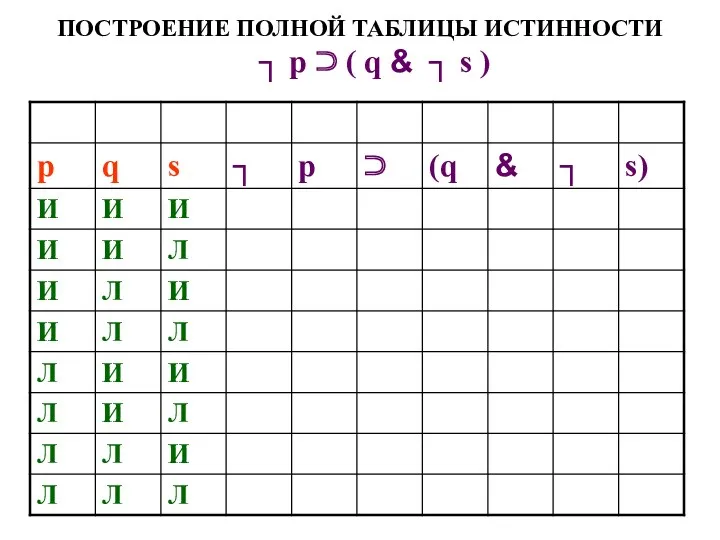
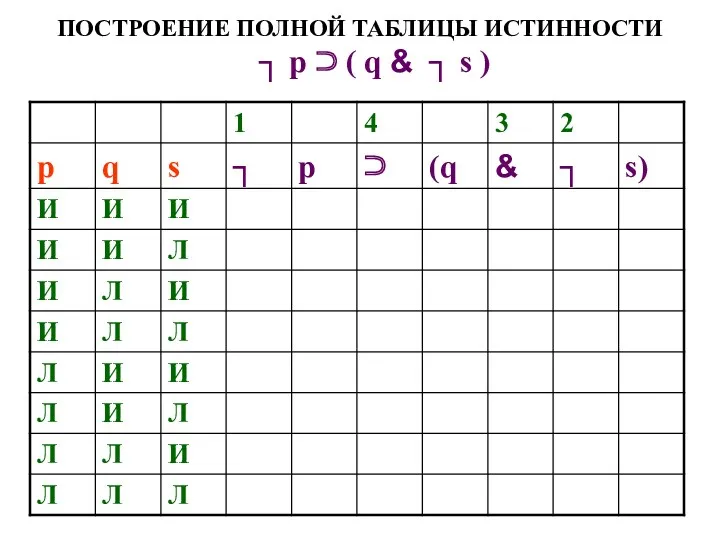
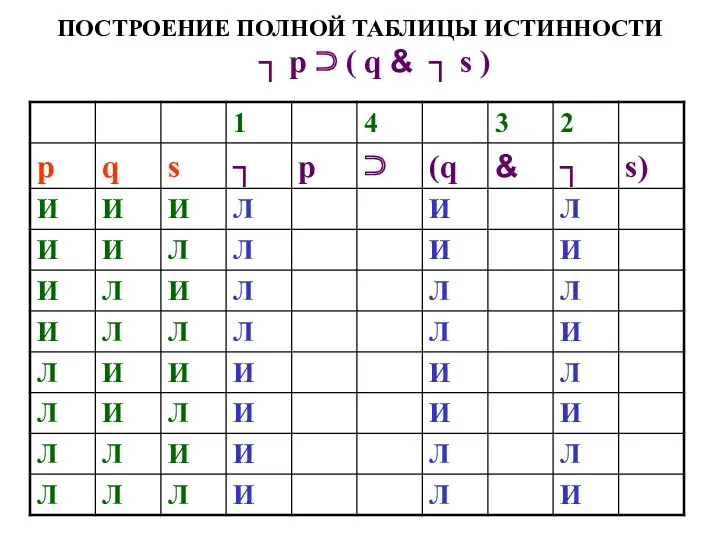
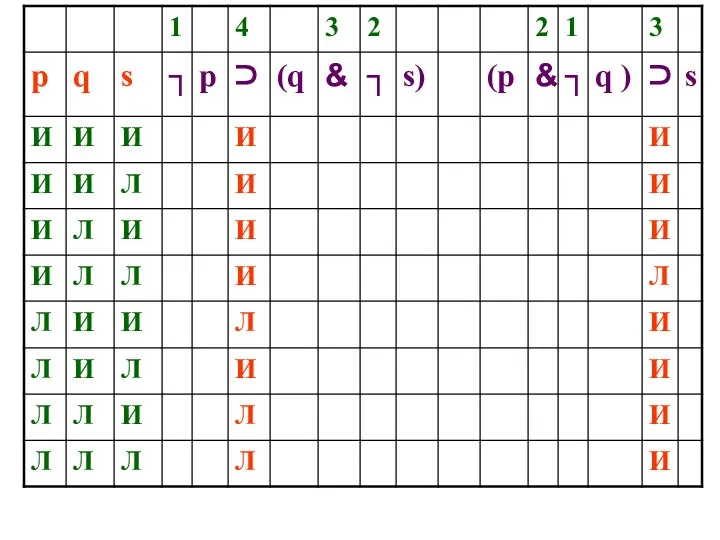
- 53. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 54. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
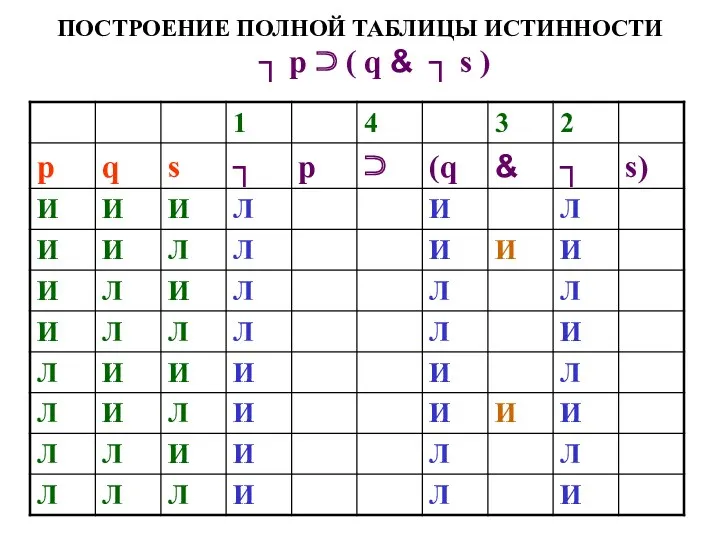
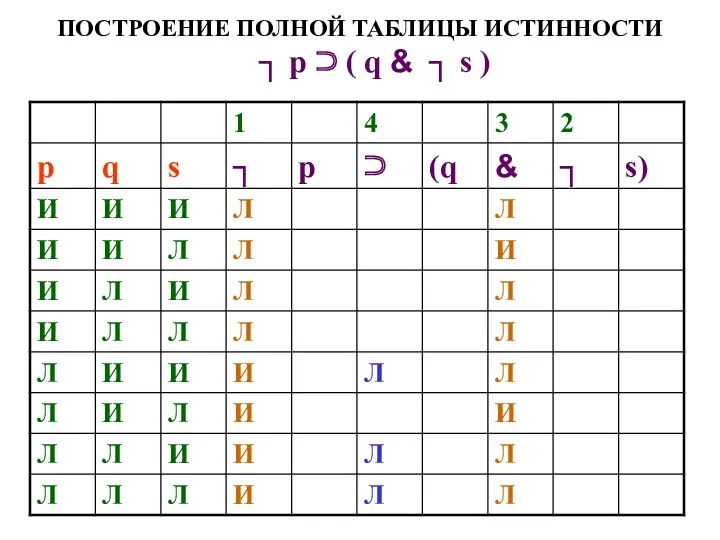
- 55. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 56. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
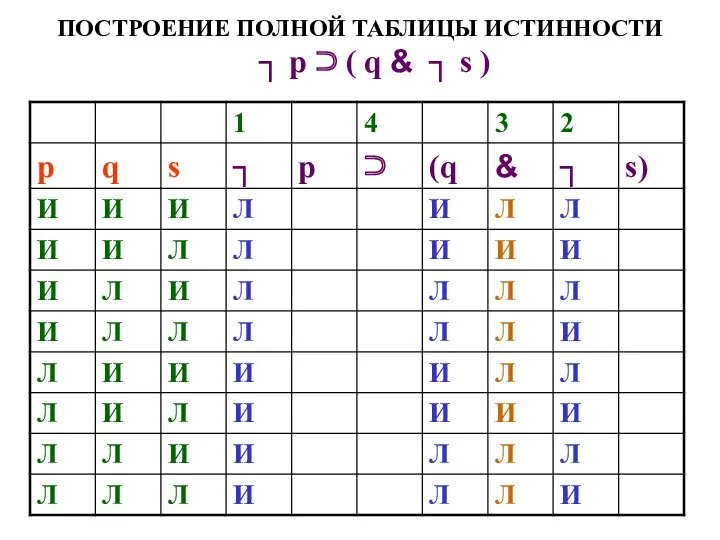
- 57. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
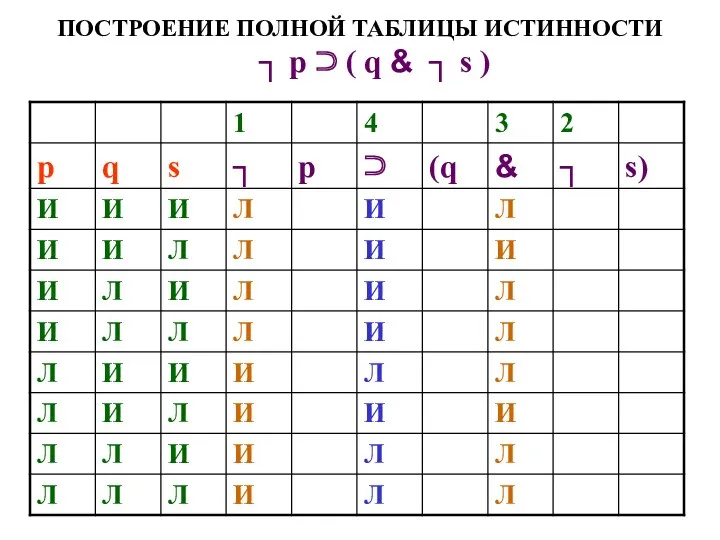
- 58. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 59. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 60. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 61. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 62. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
- 63. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s )
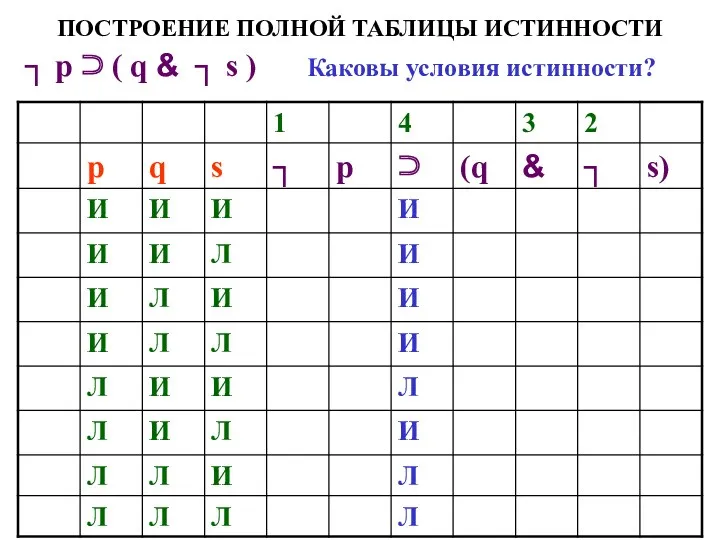
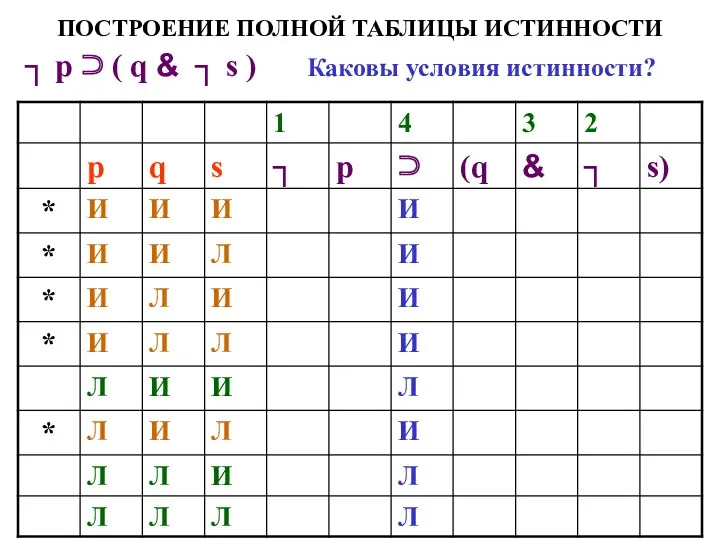
- 64. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s ) Каковы условия истинности?
- 65. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s ) Каковы условия истинности?
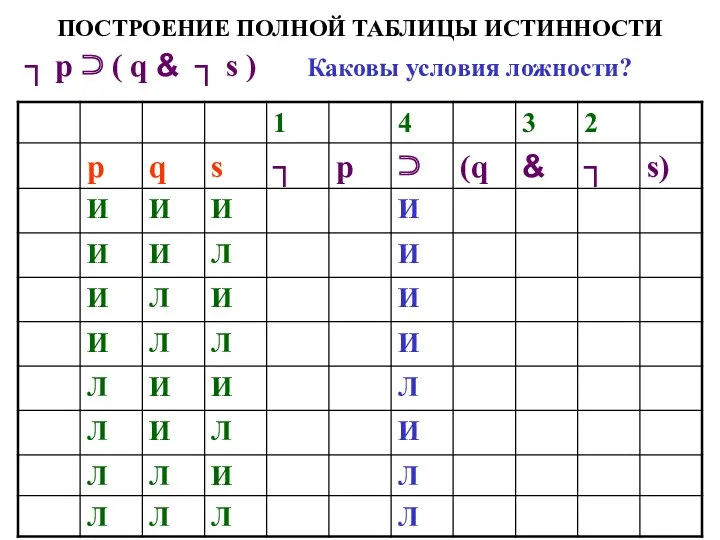
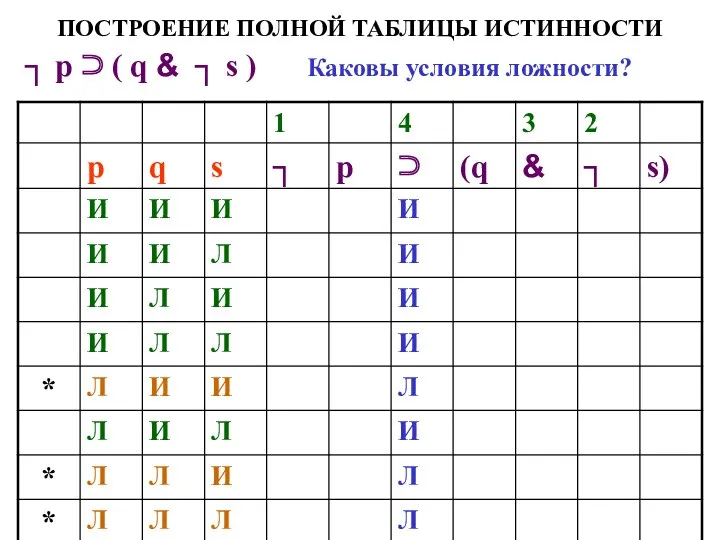
- 66. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s ) Каковы условия ложности?
- 67. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s ) Каковы условия ложности?
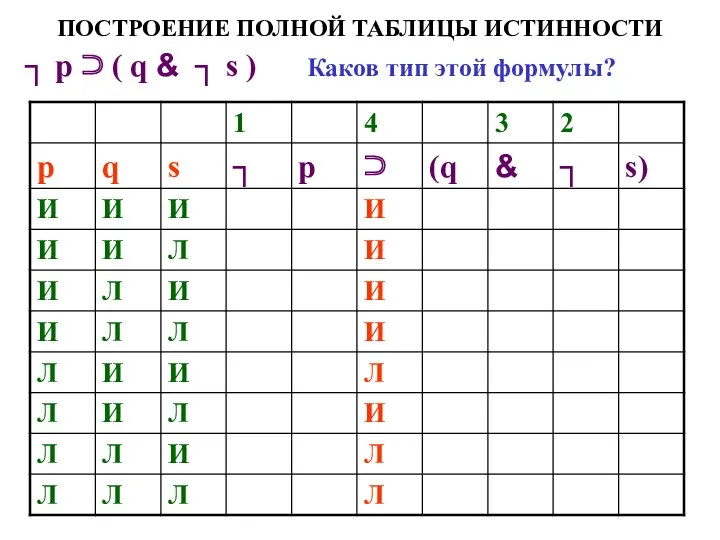
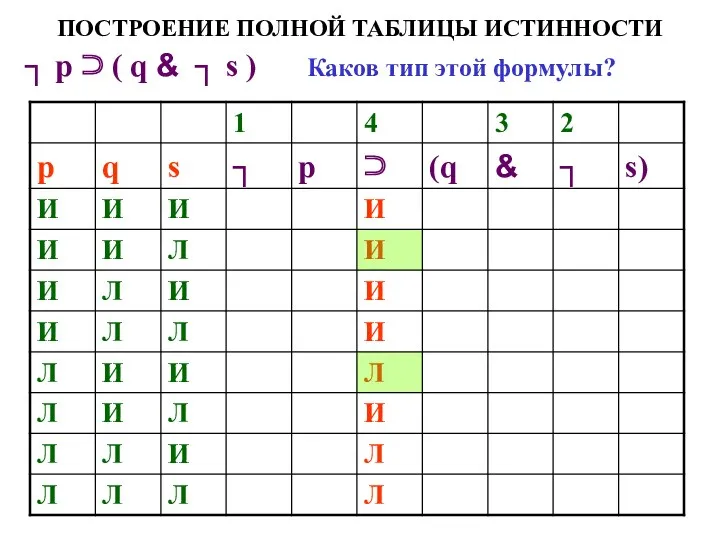
- 68. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s ) Каков тип этой
- 69. ПОСТРОЕНИЕ ПОЛНОЙ ТАБЛИЦЫ ИСТИННОСТИ ┐ р ⊃ ( q & ┐ s ) Каков тип этой
- 70. Классификация формул в логических теориях Общезначимая формула (тождественно-истинная, логический закон, логическая тавтология) – формула, принимающая значение
- 71. Классификация формул в логических теориях Тождественно-ложная формула (логическое противоречие) – формула, принимающая значение «ложь» при всех
- 72. Классификация формул в логических теориях Общезначимая формула (тождественно-истинная, логический закон, логическая тавтология) – формула, принимающая значение
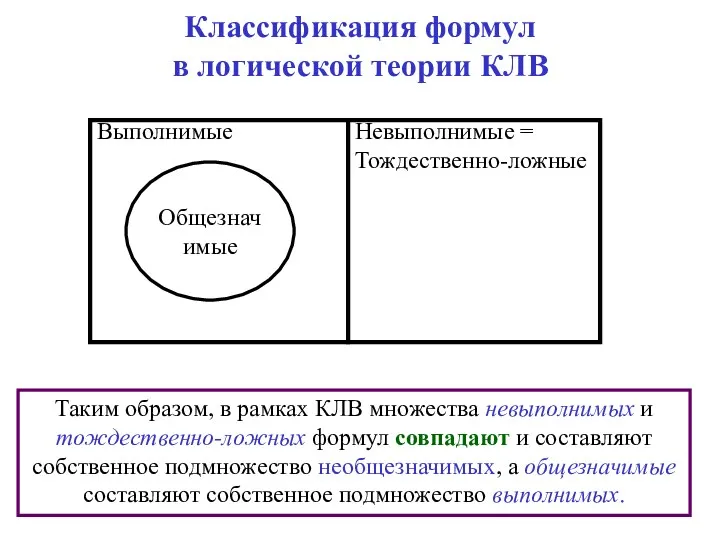
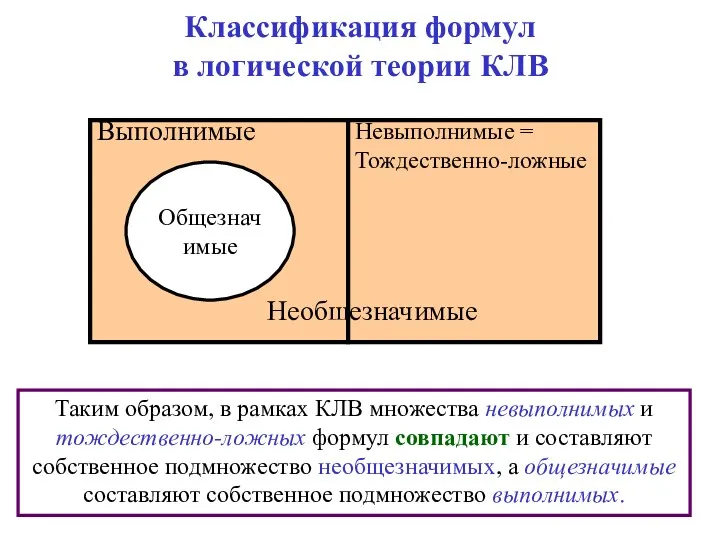
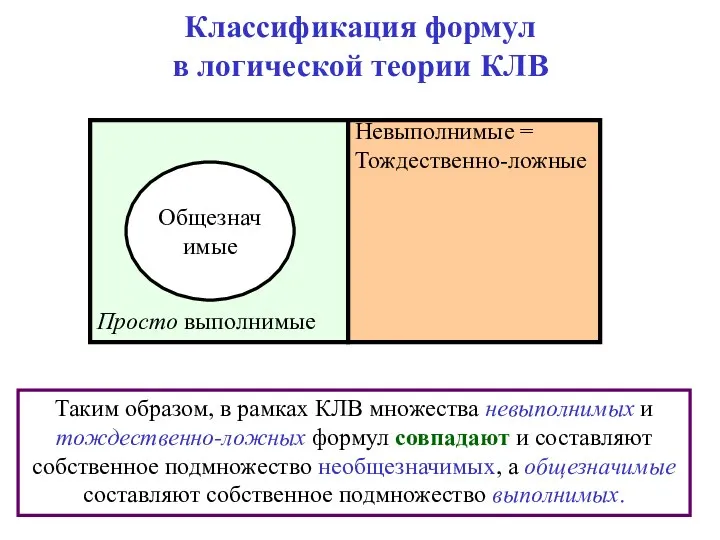
- 73. Классификация формул в логической теории КЛВ Таким образом, в рамках КЛВ множества невыполнимых и тождественно-ложных формул
- 74. Классификация формул в логической теории КЛВ Таким образом, в рамках КЛВ множества невыполнимых и тождественно-ложных формул
- 75. Классификация формул в логической теории КЛВ Таким образом, в рамках КЛВ множества невыполнимых и тождественно-ложных формул
- 76. Классификация формул в логических теориях и логическая классификация высказываний
- 77. Основные законы КЛВ Закон непротиворечия ¬ (А & ¬ А) Два противоречащих друг другу высказывания не
- 78. Основные законы КЛВ 3. Закон двойного отрицания ¬ ¬ А ≡ А Двойное отрицание высказывания равнозначно
- 79. Основные законы КЛВ 5. Закон Клавия (¬ А ⊃ А) ⊃ А Если из отрицания суждения
- 80. Основные законы КЛВ 7-8. Законы де Моргана (А & В) ≡ (¬ А ∨ ¬ В)
- 81. Основные законы КЛВ 10. Закон транзитивности (импликации) (А ⊃ В) ⊃ ((В ⊃ С) ⊃ (А
- 82. Основные законы КЛВ 12-22. Законы взаимовыразимости пропозициональных связок (А & В) ≡ ¬ (¬ А V
- 83. Основные законы КЛВ 11-22. Законы взаимовыразимости пропозициональных связок 6. (A ⊃ В) ≡ (¬ А V
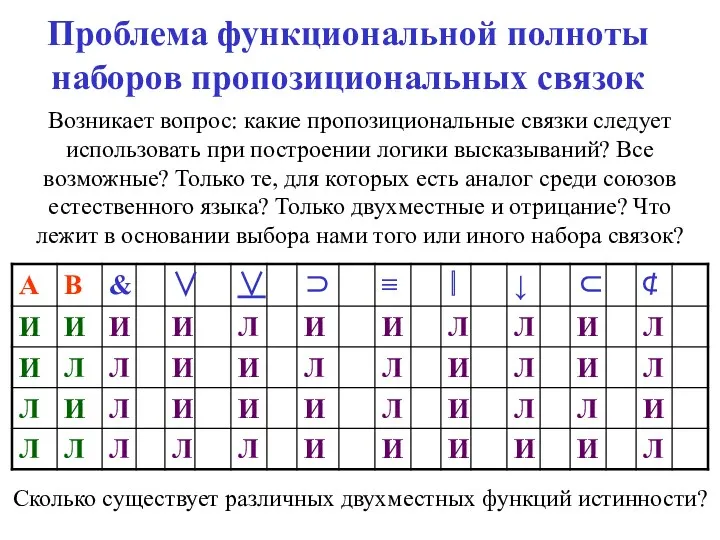
- 84. Проблема функциональной полноты наборов пропозициональных связок Возникает вопрос: какие пропозициональные связки следует использовать при построении логики
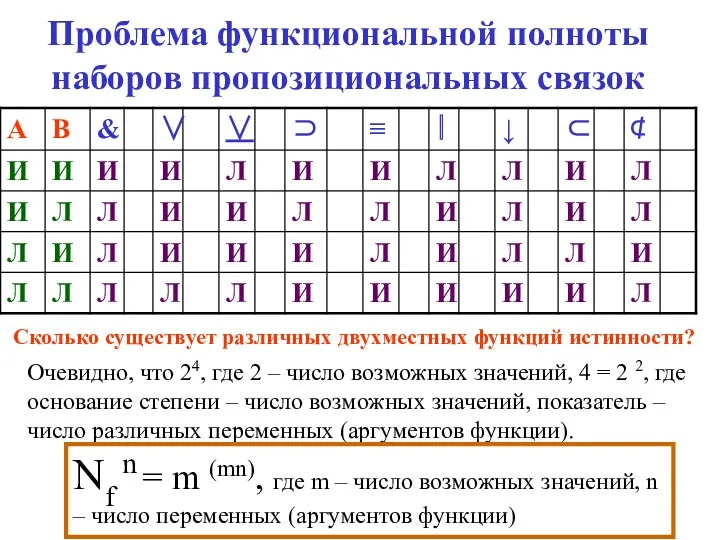
- 85. Проблема функциональной полноты наборов пропозициональных связок Очевидно, что 24, где 2 – число возможных значений, 4
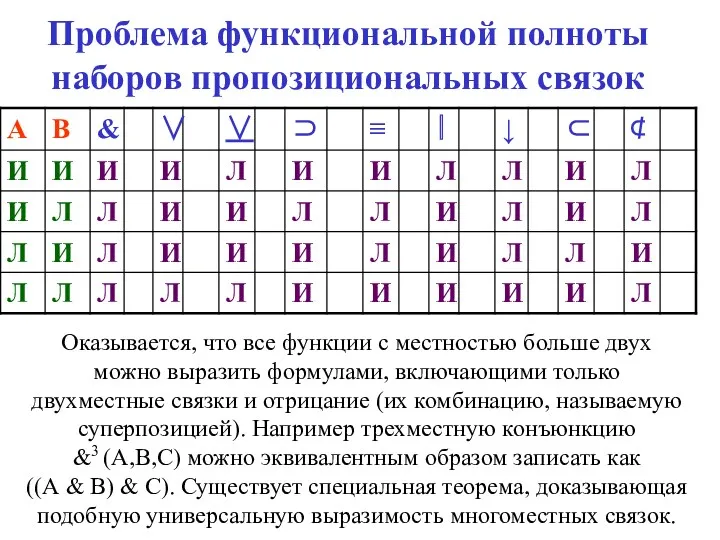
- 86. Проблема функциональной полноты наборов пропозициональных связок Оказывается, что все функции с местностью больше двух можно выразить
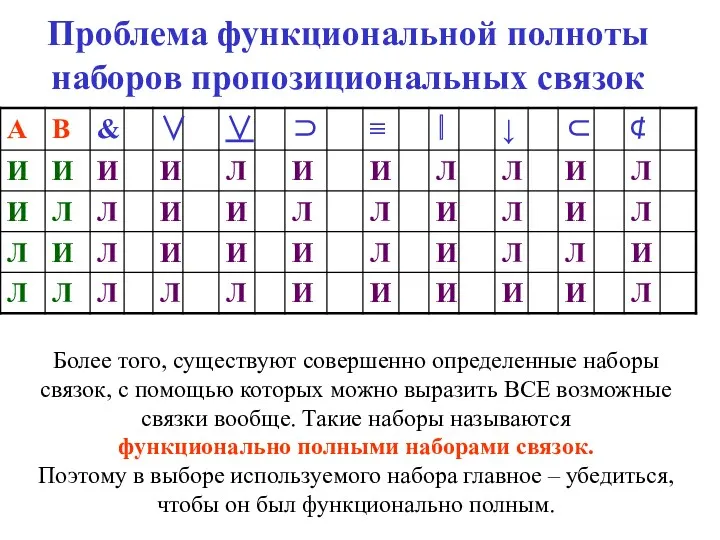
- 87. Проблема функциональной полноты наборов пропозициональных связок Более того, существуют совершенно определенные наборы связок, с помощью которых
- 88. Проблема функциональной полноты наборов пропозициональных связок ¬ (¬ А & В) ¬ А & В ¬
- 89. Проблема функциональной полноты наборов пропозициональных связок ¬ (¬ А & В) ¬ А & В ¬
- 90. Проблема функциональной полноты наборов пропозициональных связок ¬ (¬ А & В) ¬ А & В ¬
- 91. Проблема функциональной полноты наборов пропозициональных связок Если же стремиться к минимизации, то достаточно взять одну-единственную связку
- 92. Проблема функциональной полноты наборов пропозициональных связок {&, ∨, ¬} {&, ⊃, ¬} {∨, ⊃, ¬} {¬,
- 93. Основные способы правильных рассуждений в КЛВ 1. Условно-категорические умозаключения. Это двухпосылочные умозаключения, которые содержат импликативную посылку
- 94. Основные способы правильных рассуждений в КЛВ Правильные условно-категорические умозаключения. modus ponens (утверждающий способ) А ⊃ В,
- 95. Основные способы правильных рассуждений в КЛВ Правильные условно-категорические умозаключения. modus ponens (утверждающий способ) А ⊃ В,
- 96. Основные способы правильных рассуждений в КЛВ 2. Разделительно-категорические умозаключения. Эти умозаключения также являются двухпосылочными, причем в
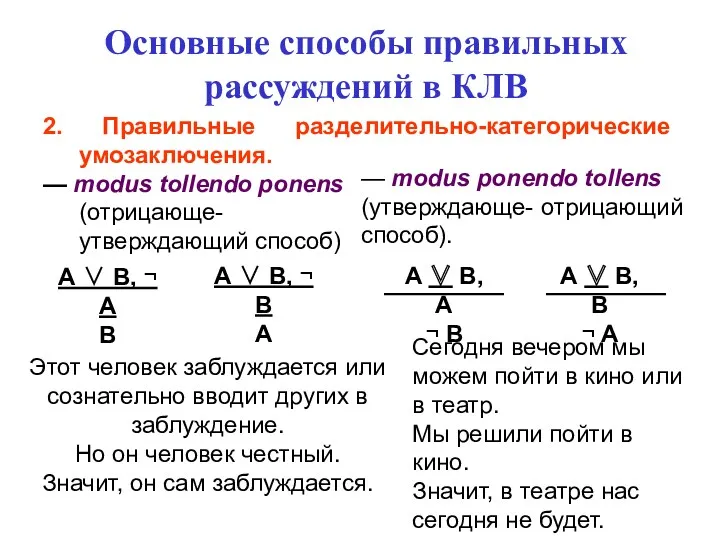
- 97. Основные способы правильных рассуждений в КЛВ 2. Правильные разделительно-категорические умозаключения. — modus tollendo ponens (отрицающе- утверждающий
- 98. Основные способы правильных рассуждений в КЛВ 2. Правильные разделительно-категорические умозаключения. — modus tollendo ponens (отрицающе- утверждающий
- 99. Основные способы правильных рассуждений в КЛВ 3. Условно-разделительные (лемматические) умозаключения. Эти умозаключения содержат несколько импликативных и
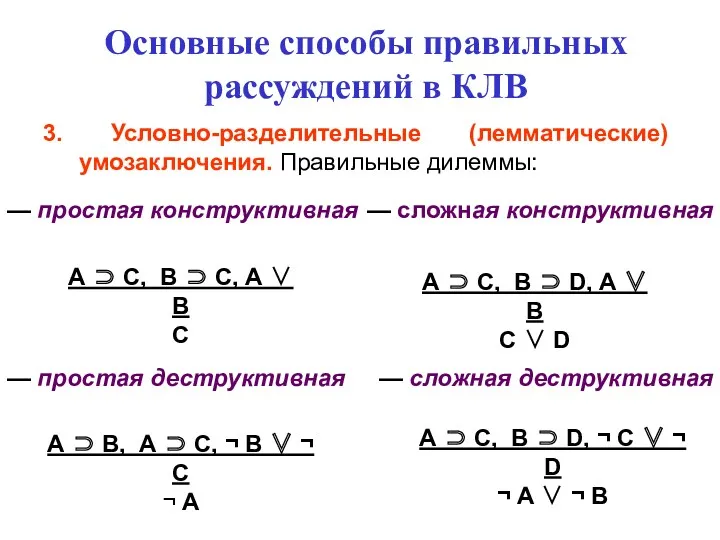
- 100. Основные способы правильных рассуждений в КЛВ 3. Условно-разделительные (лемматические) умозаключения. Правильные дилеммы: А ⊃ С, В
- 101. Основные способы правильных рассуждений в КЛВ 3. Условно-разделительные (лемматические) умозаключения. Правильные дилеммы: А ⊃ С, В
- 102. Основные способы правильных рассуждений в КЛВ 3. Условно-разделительные (лемматические) умозаключения. Правильные дилеммы: — сложная деструктивная —
- 103. Основные способы правильных рассуждений в КЛВ Все приведенные схемы относились к числу прямых способов аргументации, при
- 104. ОСНОВНЫЕ ВИДЫ НЕПРЯМЫХ СПОСОБОВ АРГУМЕНТАЦИИ 1. Рассуждение по правилу дедукции Из Г и А выведено В
- 105. ОСНОВНЫЕ ВИДЫ НЕПРЯМЫХ СПОСОБОВ АРГУМЕНТАЦИИ Из Г и А выведено ⊥ Из Г выведено ¬А 4.
- 106. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) У нас имеется автоматическое устройство, имеющее механизмы А, В и С.
- 107. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) Логические отношения между формулами устанавливаются в зависимости от соотношения тех значений
- 108. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) Установить логические отношения – это значит ответить на один или несколько
- 109. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) Возможно ли такое положение вещей, при котором обе формулы принимают значение
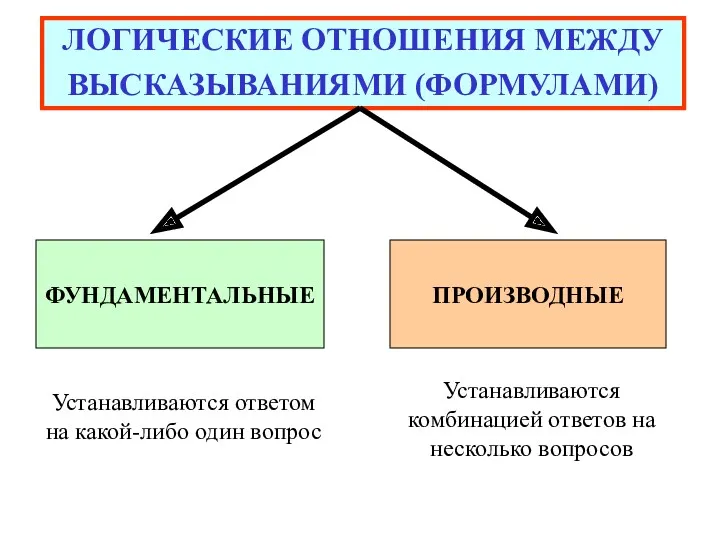
- 110. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) ПРОИЗВОДНЫЕ ФУНДАМЕНТАЛЬНЫЕ Устанавливаются ответом на какой-либо один вопрос Устанавливаются комбинацией ответов
- 111. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) ФУНДАМЕНТАЛЬНЫЕ Устанавливаются ответом на какой-либо один вопрос 1 – (не) совместимость
- 112. ФУНДАМЕНТАЛЬНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ 1 – (не) совместимость по истинности 2 – (не) совместимость по
- 113. ФУНДАМЕНТАЛЬНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ Х╞ Y, если и только если не существует такой интерпретации параметров,
- 114. ФУНДАМЕНТАЛЬНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ Х1...Хn╞ Y, если и только если не существует такой интерпретации параметров,
- 115. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ВЫСКАЗЫВАНИЯМИ (ФОРМУЛАМИ) 1 – противоречие 2 – противоположность 3 – подпротивоположность 4 –
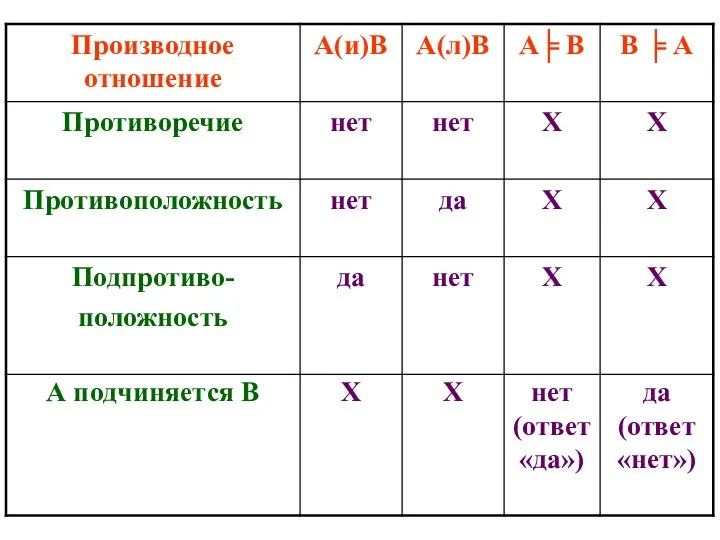
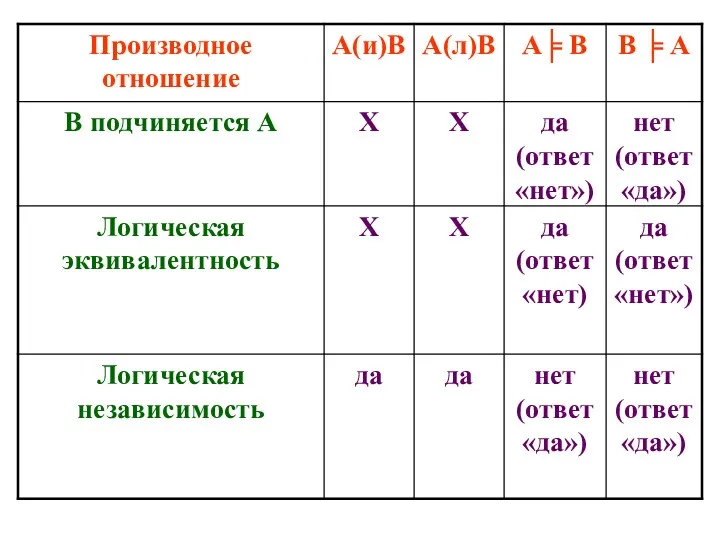
- 116. ПРОИЗВОДНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ 1. Формулы А и В находятся в отношении противоречия (контрадикторности), если
- 117. ПРОИЗВОДНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ 3. Формулы А и В находятся в отношении подпротивоположности (субконтрарности), если
- 118. ПРОИЗВОДНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ 5. Формулы А и В находятся в отношении логической эквивалентности, если
- 119. ПРОИЗВОДНЫЕ ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ФОРМУЛАМИ 1 – противоречие 2 – противоположность 3 – подпротивоположность 4 –
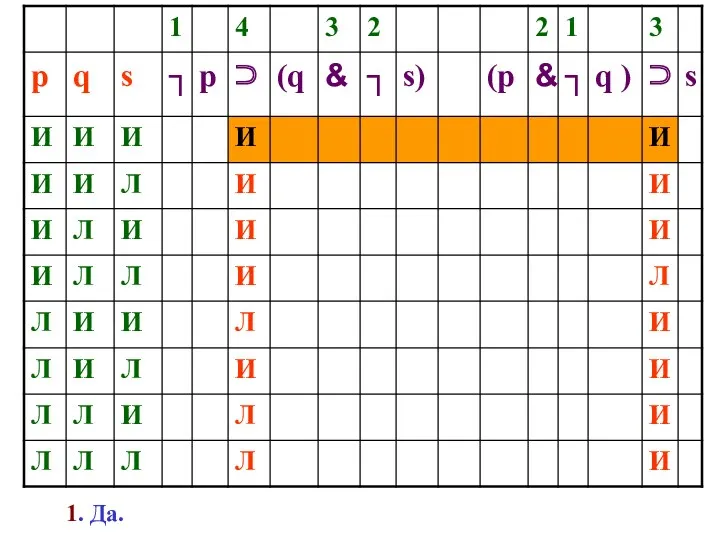
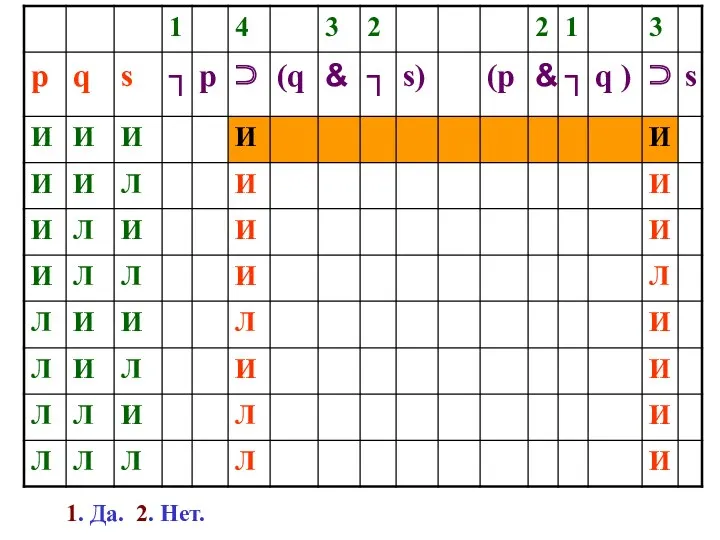
- 122. УСТАНОВЛЕНИЕ ЛОГИЧЕСКИХ ОТНОШЕНИЙ Алгоритм установления Л.О. между двумя формулами: построение совместной таблицы истинности Установим, в каких
- 125. 1. Да.
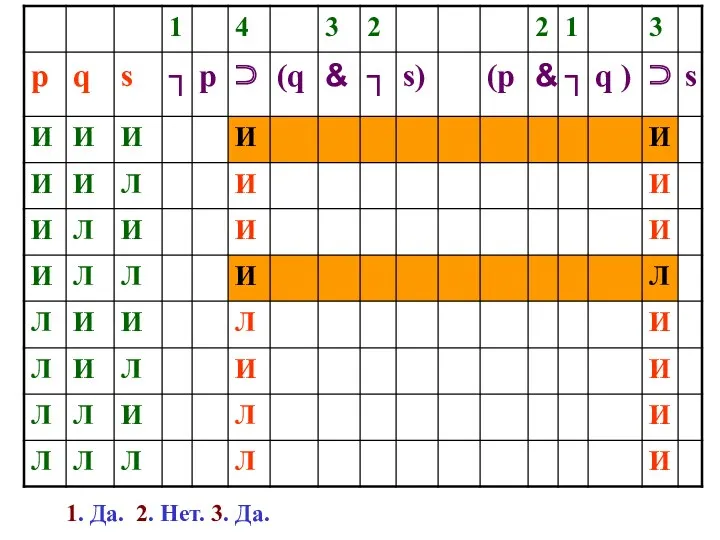
- 126. 1. Да. 2. Нет.
- 127. 1. Да. 2. Нет. 3. Да.
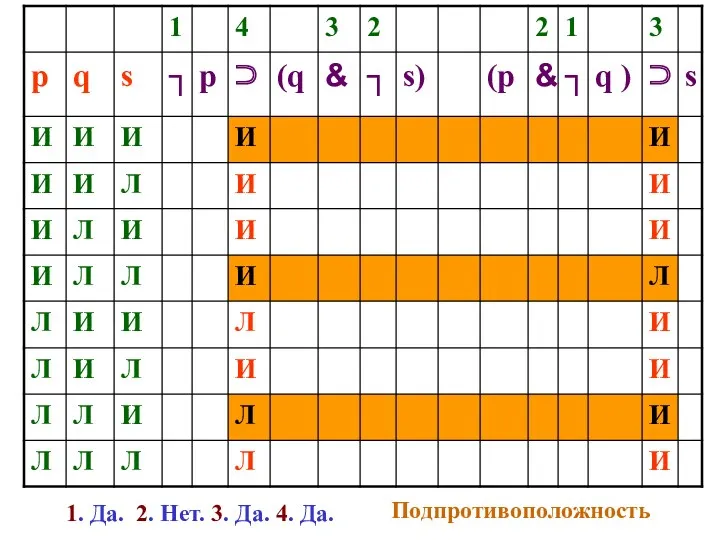
- 128. 1. Да. 2. Нет. 3. Да. 4. Да. Подпротивоположность
- 129. ПРОВЕРКА УМОЗАКЛЮЧЕНИЙ ТАБЛИЧНЫМ МЕТОДОМ Умозаключение является правильным тогда и только тогда, когда из его посылок логически
- 130. Если в мире есть справедливость, злые люди не могут быть счастливы. Если мир сотворил злой гений,
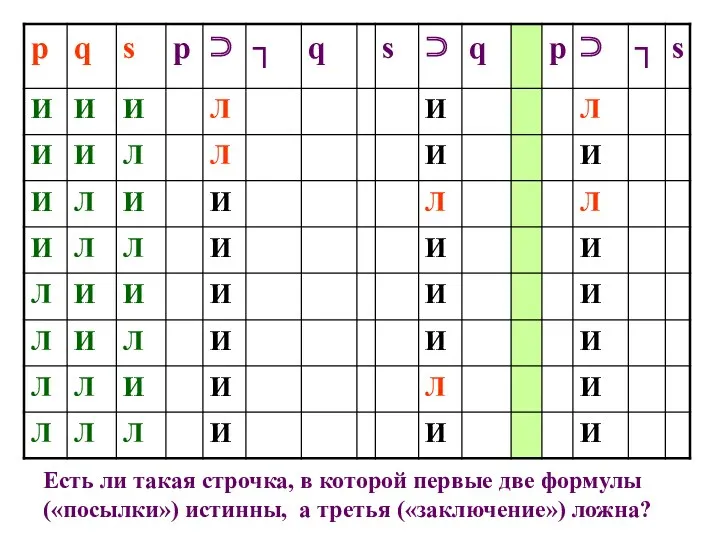
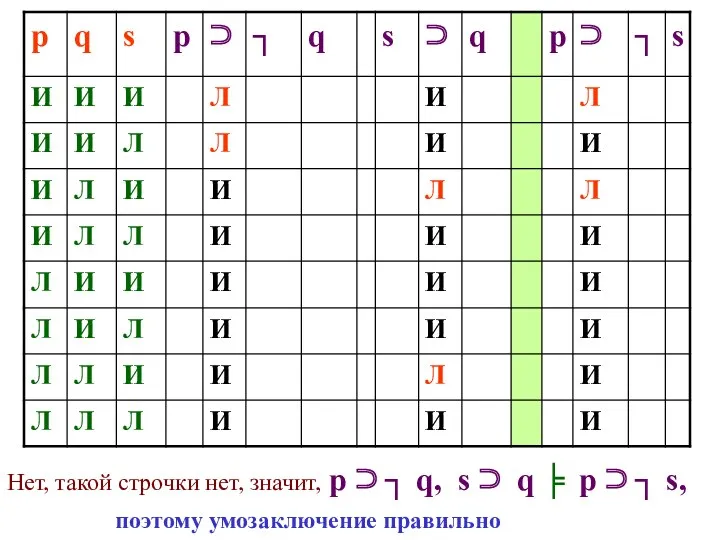
- 131. Есть ли такая строчка, в которой первые две формулы («посылки») истинны, а третья («заключение») ложна?
- 132. Нет, такой строчки нет, значит, р ⊃ ┐ q, s ⊃ q ╞ р ⊃ ┐
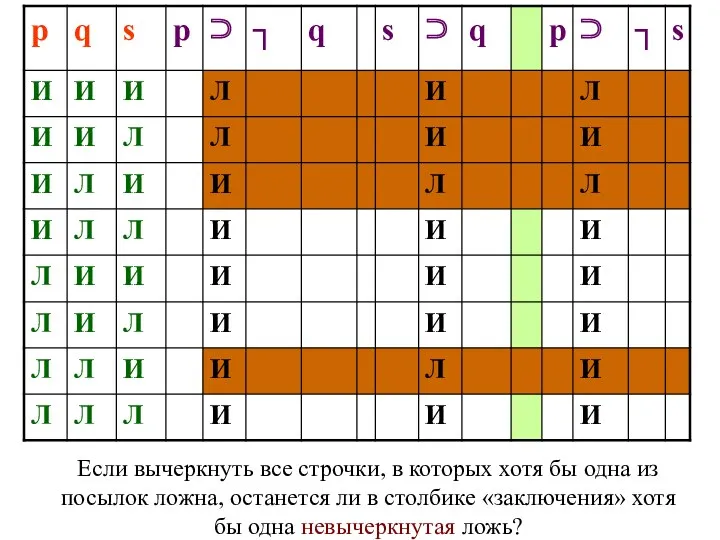
- 133. Если вычеркнуть все строчки, в которых хотя бы одна из посылок ложна, останется ли в столбике
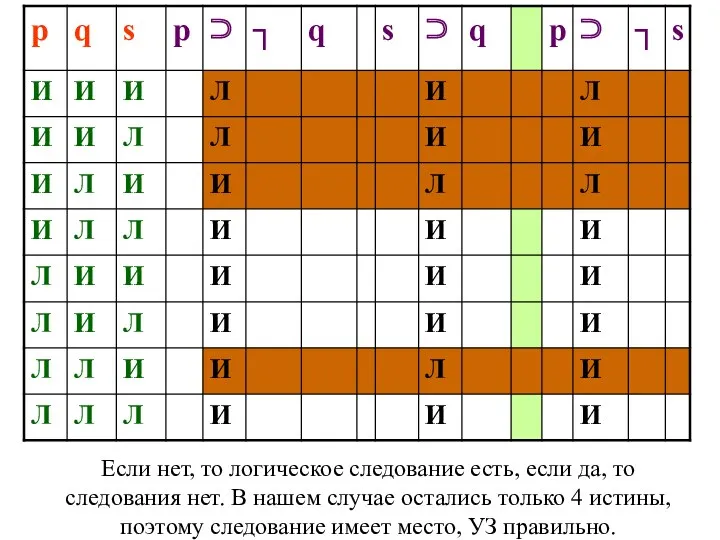
- 134. Если нет, то логическое следование есть, если да, то следования нет. В нашем случае остались только
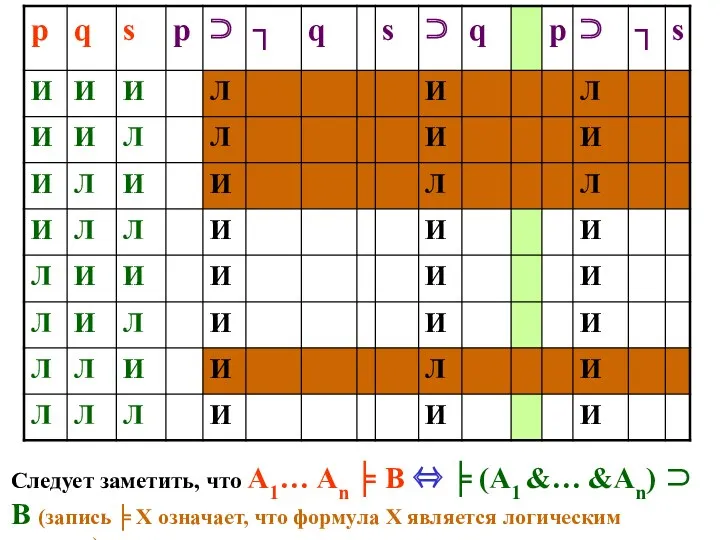
- 135. Следует заметить, что А1… Аn ╞ В ⇔ ╞ (А1 &… &Аn) ⊃ В (запись ╞
- 136. ПОНЯТИЯ НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЙ Сравним два высказывания: Холмс играет на скрипке, когда у него лирическое
- 137. ПОНЯТИЯ НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЙ Событие А называется необходимым условием для события В, если без события
- 138. ПОНЯТИЯ НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЙ Событие А называется необходимым условием для события В, если без события
- 139. ПОНЯТИЯ НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЙ ┐А ⊃ ┐В, или В ⊃ А (необходимое условие ставится в
- 140. «Парадоксы следования» в классической логике Х1...Хn╞ Y, если и только если не существует такой интерпретации параметров,
- 141. «Парадоксы следования» в классической логике Х1...Хn╞ Y, если и только если не существует такой интерпретации параметров,
- 142. «Парадоксы следования» в классической логике ⊥ ╞ Y – из противоречия следует все, что угодно Х
- 144. Скачать презентацию

































































































 Смысл действия деления
Смысл действия деления Решение уравнений. 6 класс
Решение уравнений. 6 класс Реальная математика. ОГЭ
Реальная математика. ОГЭ Приём вычитания вида 12 -
Приём вычитания вида 12 - Многогранники и круглые тела
Многогранники и круглые тела Пропорция. Урок в 6 классе
Пропорция. Урок в 6 классе Матрицы и действия над ними
Матрицы и действия над ними Координатная плоскость. 7 класс
Координатная плоскость. 7 класс Координаты на прямой
Координаты на прямой Зачем нужны отрицательные числа? Примеры применения отрицательных чисел
Зачем нужны отрицательные числа? Примеры применения отрицательных чисел Отрезок. Треугольник. Многоугольники
Отрезок. Треугольник. Многоугольники Состав двузначных чисел(Математика 2 класс)
Состав двузначных чисел(Математика 2 класс) Окружность – замкнутая линия
Окружность – замкнутая линия Теорема про три перпендикуляри
Теорема про три перпендикуляри Организация современного урока математики в условиях реализации ФГОС
Организация современного урока математики в условиях реализации ФГОС Первісна. Таблиця первісних. Невизначений інтеграл
Первісна. Таблиця первісних. Невизначений інтеграл Умножение одночлена на многочлен
Умножение одночлена на многочлен Пересечение множеств
Пересечение множеств Исследование операций в логистике
Исследование операций в логистике Теорема Пифагора. Пифагор Самосский
Теорема Пифагора. Пифагор Самосский Итоговое повторение курса алгебры за 8 класс
Итоговое повторение курса алгебры за 8 класс Математика.Тема урока: Числа от 1 до 10.
Математика.Тема урока: Числа от 1 до 10. Прямоугольная система координат. Координаты вектора
Прямоугольная система координат. Координаты вектора Решение задач по теории вероятности в заданиях ЕГЭ
Решение задач по теории вероятности в заданиях ЕГЭ Алгебра
Алгебра Игра Экология и математика
Игра Экология и математика Счет в пределах 10
Счет в пределах 10 Признаки равенства прямоугольных треугольников. 7 класс
Признаки равенства прямоугольных треугольников. 7 класс