Содержание
- 2. Математическое ожидание и дисперсия с.в., распределенной по биномиальному закону. Теорема. Пусть Тогда E(X)=np, D(X)=npq, где q=1-p.
- 3. . D(Xi)=E(Xi2)-E2(Xi)= p-p2 = p(1-p) =pq. E(Xi2)=p; Представим Х=Х1+Х2+…+Хn , D(X)=?
- 4. Пр. В Петербурге в течении трех дней наблюдается наводнение. Вероятность того, что в каждый из этих
- 5. Решение. n=3, p=0,8 q=0,2; P{X=0}=q3=0,008; P{X=1}=C31p q2=3*0,8*0,22=0,096; P{X=2}=C32p2 q1=3*0,82*0,2=0,384; P{X=3}=р3 =0,512; E(X)=np=3*0,8=2,4; D(X)=npq=3*0,8*0,2=0,48; (n+1)p=4*0,8=3,2; m0=[3,2]=3;
- 6. §2. Распределение Пуассона Опр. Д.с.в. Х имеет распределение Пуассона с параметром λ>0, если она принимает значения
- 7. D(X)=E(X2)-E2(X). E2(X)=λ2,
- 9. Пример 1
- 11. Скачать презентацию



![Решение. n=3, p=0,8 q=0,2; P{X=0}=q3=0,008; P{X=1}=C31p q2=3*0,8*0,22=0,096; P{X=2}=C32p2 q1=3*0,82*0,2=0,384; P{X=3}=р3 =0,512; E(X)=np=3*0,8=2,4; D(X)=npq=3*0,8*0,2=0,48; (n+1)p=4*0,8=3,2; m0=[3,2]=3;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119021/slide-4.jpg)

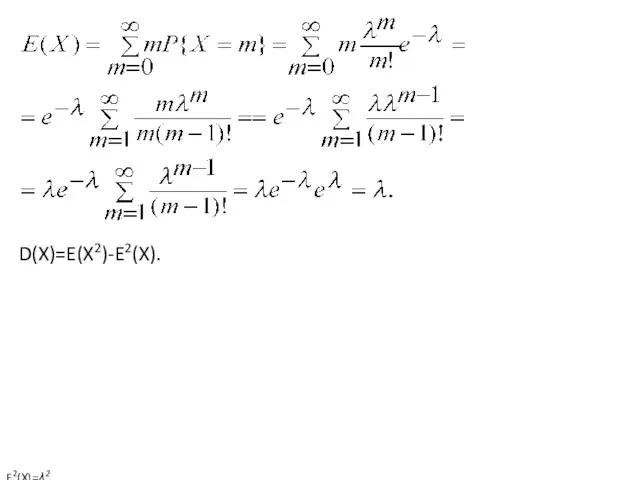


 Двойной интеграл: определение, свойства, вычисление в ПДСК
Двойной интеграл: определение, свойства, вычисление в ПДСК Числовые равенства и неравенства
Числовые равенства и неравенства Нормальное распределение
Нормальное распределение Интерактивный тренажёр-игра по теме Формулы. 5 класс
Интерактивный тренажёр-игра по теме Формулы. 5 класс Сложение и вычитание в пределах 20. Тренажер
Сложение и вычитание в пределах 20. Тренажер Урок по математике на тему Таблица умножения на 2
Урок по математике на тему Таблица умножения на 2 Математичсекий тест для дошколят
Математичсекий тест для дошколят Решение задач по краткому условию. 2 класс
Решение задач по краткому условию. 2 класс Функция y=k/x, её график и свойства
Функция y=k/x, её график и свойства Приемы устных вычислений. Формирование навыков устных вычислений на уроках математики
Приемы устных вычислений. Формирование навыков устных вычислений на уроках математики Состав числа 10. Урок математики
Состав числа 10. Урок математики Многочлен и его стандартный вид
Многочлен и его стандартный вид Проектная задача Покупка учебников общешкольным родительским комитетом
Проектная задача Покупка учебников общешкольным родительским комитетом Применение нестандартных форм и методов обучения в 5 -6 классах
Применение нестандартных форм и методов обучения в 5 -6 классах Как называется горизонтальная ось?
Как называется горизонтальная ось? Surface area and volumes
Surface area and volumes Линейные пространства
Линейные пространства Дискретная математика
Дискретная математика Решение планиметрических многовариантных задач
Решение планиметрических многовариантных задач Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Арифметическая прогрессия
Арифметическая прогрессия Математический турнир. Презентация.
Математический турнир. Презентация. Числовые последовательности
Числовые последовательности Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы
Уокс әсерінің улы концентрациясына және оның әрекет ету уақытына тәуелділігін зерттеуде. Габер формуласы Понятие многогранника. Призма
Понятие многогранника. Призма Состав чисел до 10
Состав чисел до 10 Сложение дробей с одинаковыми знаменателями
Сложение дробей с одинаковыми знаменателями Перпендикулярность прямой и плоскости. Задания для устного счета. Упражнение 7
Перпендикулярность прямой и плоскости. Задания для устного счета. Упражнение 7