Содержание
- 2. План лекции: Задачи математической статистики. Генеральная и выборочная совокупности Основные этапы исследования Дискретные и интервальные ряды
- 3. Что такое математическая статистика? Математическая статистика – это наука извлечения полезной информации из данных, полученных в
- 4. Наиболее общую совокупность, подлежащих изучению объектов называют генеральной. Выборка считается репрезентативной, если каждый объект выборки отобран
- 5. Основные понятия математической статистики Объемом выборки называют число объектов этой совокупности. Таким образом, вместо большой совокупности
- 6. Результаты, полученные при изучении выборки, распространяются на объекты всей генеральной совокупности. Для этого выборка должна быть
- 7. Какие задачи нас интересуют? определение закона распределения случайной величины по выборочным данным; задача проверки правдоподобия гипотез
- 8. Основные этапы исследования: Сгруппировать исследуемый ряд по классам. Подсчитать середины интервалов и частоты попадания в интервал.
- 9. Статистическое распределение выборки и его характеристики Пусть из генеральной совокупности извлечена выборка, причем x1 наблюдалось n1
- 10. Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения x относительную частоту
- 11. Интервальная оценка (доверительный интервал) для генеральной средней Интервальной называют оценку, которая определяется двумя числами– концами интервала.
- 12. Статистическая функция распределения случайной величины Х Рассмотрим эксперимент, который поможет понять смысл этой функции: Дана некоторая
- 13. Пример:Ряд распределения студентов по росту 148 158 149 162 170 156 186 151 161 152 171
- 14. Размах распределения Из имеющихся значений признака Х выбирают наименьшее (Хmin), наибольшее (Хmax), определяют размах распределения (Хmax
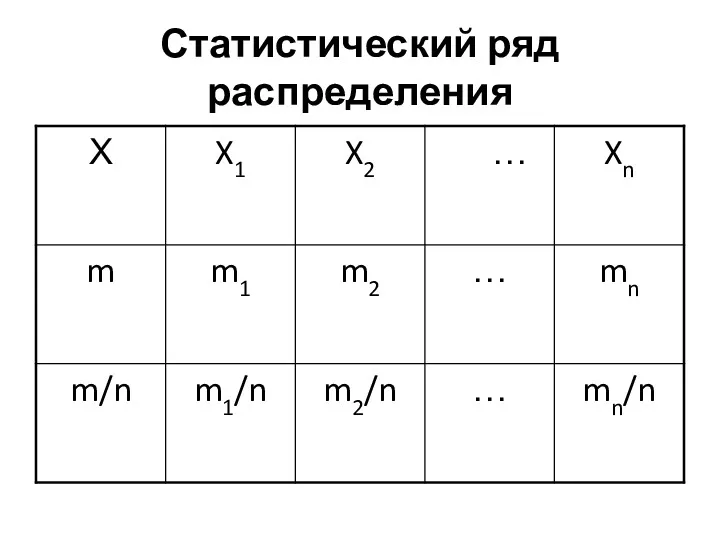
- 15. Статистический ряд распределения
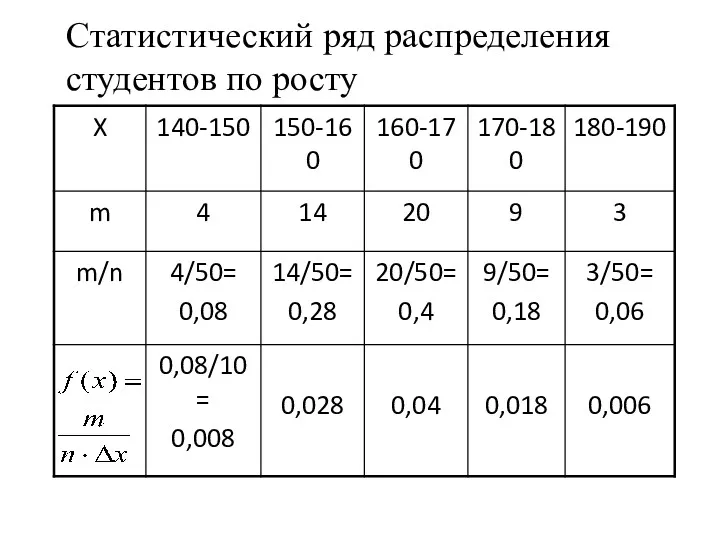
- 16. Статистический ряд распределения студентов по росту
- 17. Гистограмма распределения студентов по росту (m, m/n, f(x))
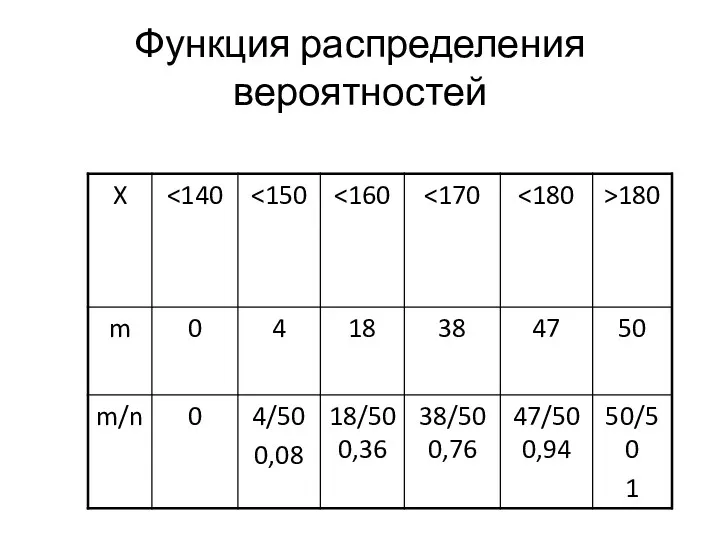
- 18. Функция распределения вероятностей
- 19. График F(x)
- 20. Точечные характеристики случайной величины :выборочное среднее, дисперсия и СКО
- 21. Непараметрические характеристики: мода и медиана Me-медиана Варианта, которая делит ряд пополам 158, 164, 172, 175, 175,
- 22. Непараметрические характеристики: мода и медиана Mo-наиболее часто встречающаяся варианта 158, 164, 172, 175, 175, 175, 179,
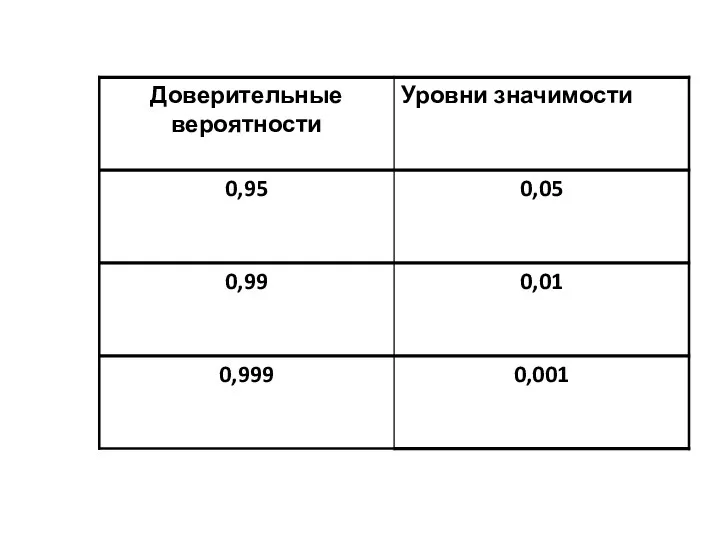
- 24. Доверительные вероятности и доверительные интервалы Вероятности 0,95 и 0,99 (95% и 99%) – доверительные вероятности Δх=±σt
- 25. Уровни значимости Определенным значениям доверительных вероятностей соответствуют так называемые уровни значимости (α). Уровень значимости обозначает вероятность
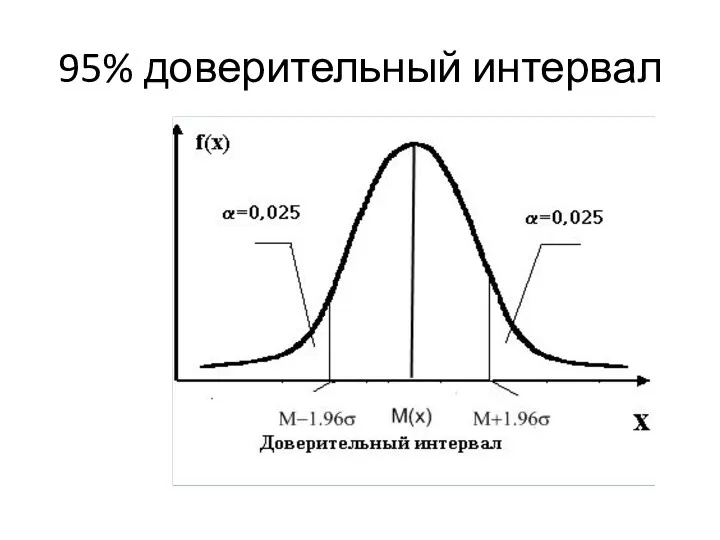
- 27. 95% доверительный интервал
- 28. Задача: Найти доверительный интервал для роста студентов с вероятностью p=0,95 (α=0,05); M(x)=170 см, σ=5 см Δх=1,96⋅5≈10
- 29. Нормальный закон распределения случайных величин Нормальное распределение возникает тогда, когда на изменение случайной величины действует множество
- 30. Говорят, что X имеет нормальное (гауссовское) распределение с параметрами μ и σ , где μ∈R, σ>0,
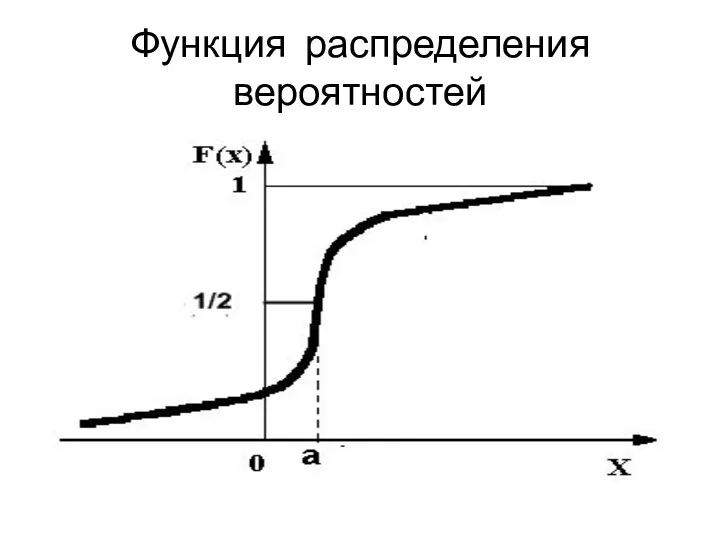
- 31. Функция распределения вероятностей интегральная функция распределения
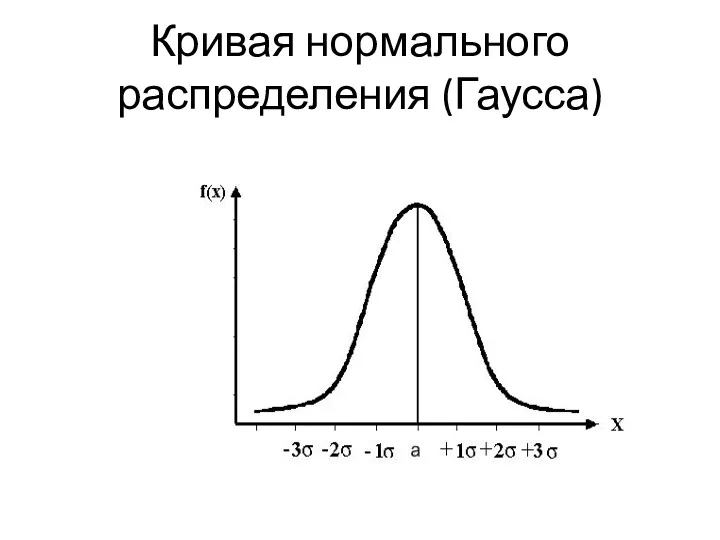
- 32. Кривая нормального распределения (Гаусса)
- 33. Функция распределения вероятностей
- 34. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ: Параметр μ характеризует математическое ожидание (среднее арифметическое) случайной величины, являясь центром распределения и наиболее
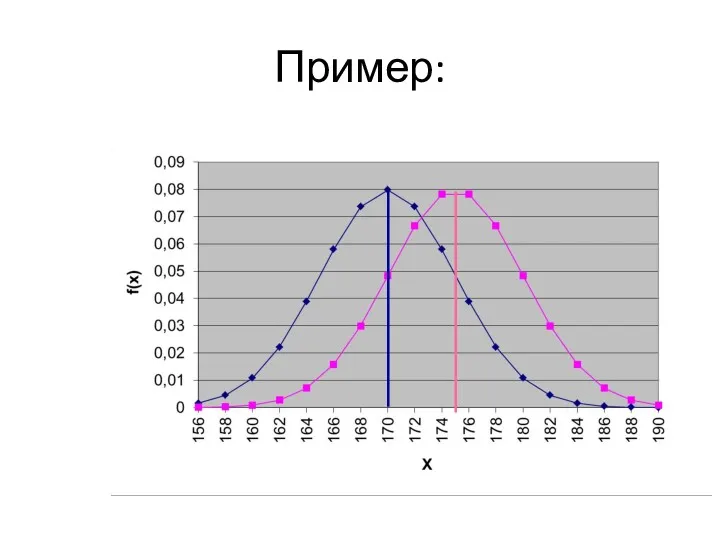
- 35. Пример:
- 36. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ: Параметр σ характеризует изменчивость случайной величины (меру растянутости кривой вдоль оси x): чем больше
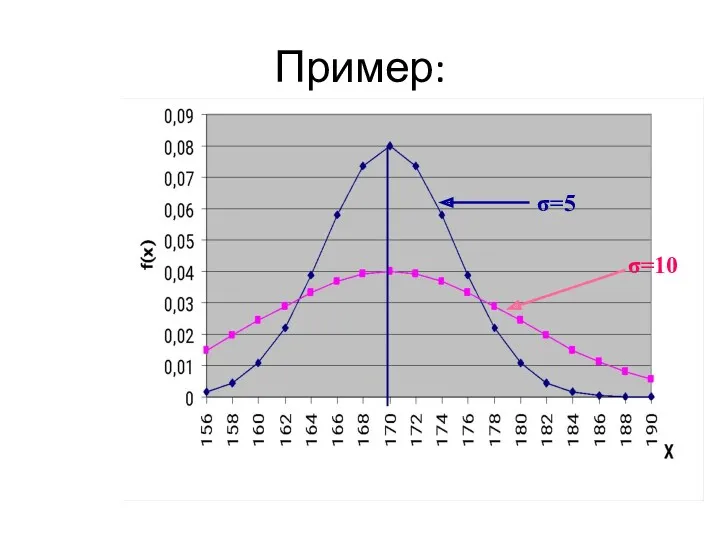
- 37. Пример: σ=10 σ=5
- 38. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ: График нормальной кривой симметричен относительно прямой x=μ (одинаковые по абсолютной величине отрицательные и положительные
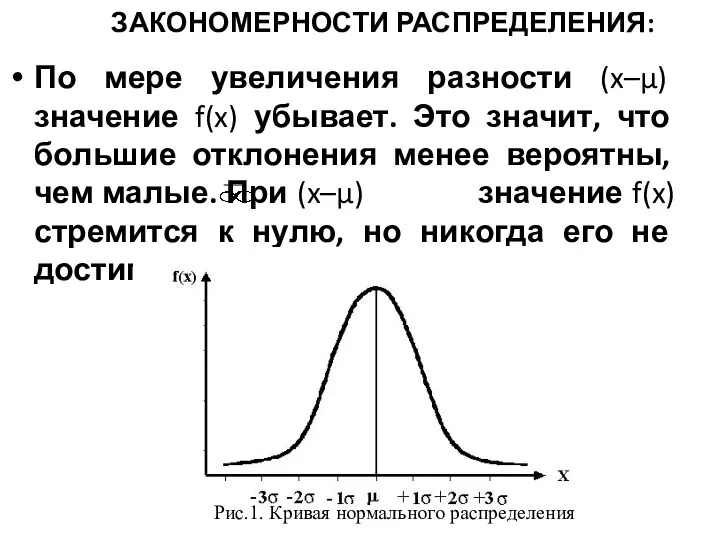
- 39. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ: По мере увеличения разности (x–μ) значение f(x) убывает. Это значит, что большие отклонения менее
- 40. Функция нормального закона функция плотности распределения вероятностей функция распределения вероятностей
- 41. Вероятность попадания значения случайной величины в интервал от а до b: причем Ф(–t) = 1– Ф(t)
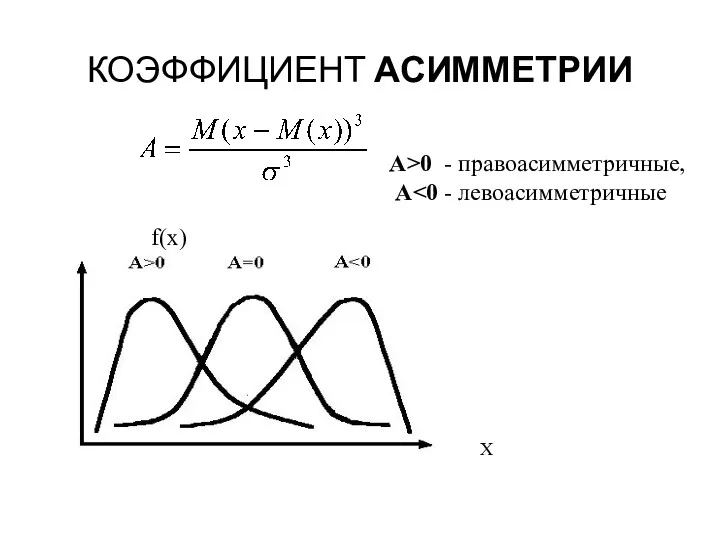
- 42. КОЭФФИЦИЕНТ АСИММЕТРИИ А>0 - правоасимметричные, А f(x) X
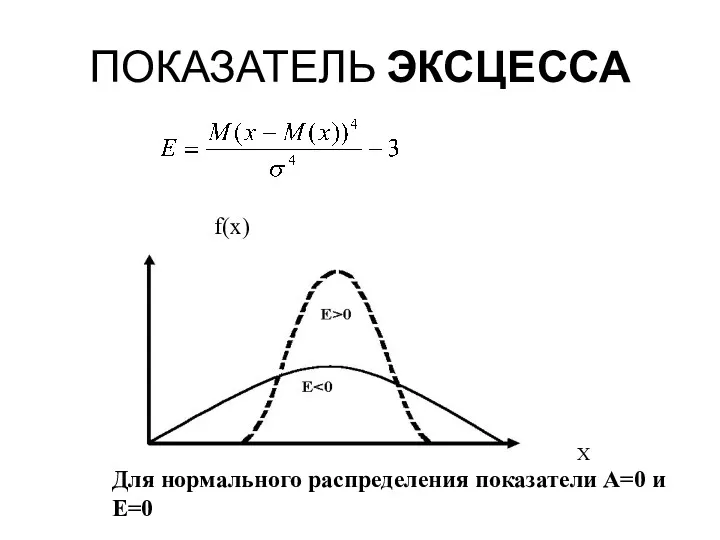
- 43. ПОКАЗАТЕЛЬ ЭКСЦЕССА f(x) Х Для нормального распределения показатели А=0 и Е=0
- 44. Задача: Записать функции нормального закона для распределения студентов по росту: M(X)=170 см; σ=5 см
- 45. Нормальное распределение с параметрами M(x)=0 и σ=1 называется стандартным N0,1 (нормированным нормальным распределением) Функция плотности распределения
- 46. Нормированное отклонение: Нормированным отклонением называется отклонение случайной величины x,от её математического ожидания, выраженное в единицах σ
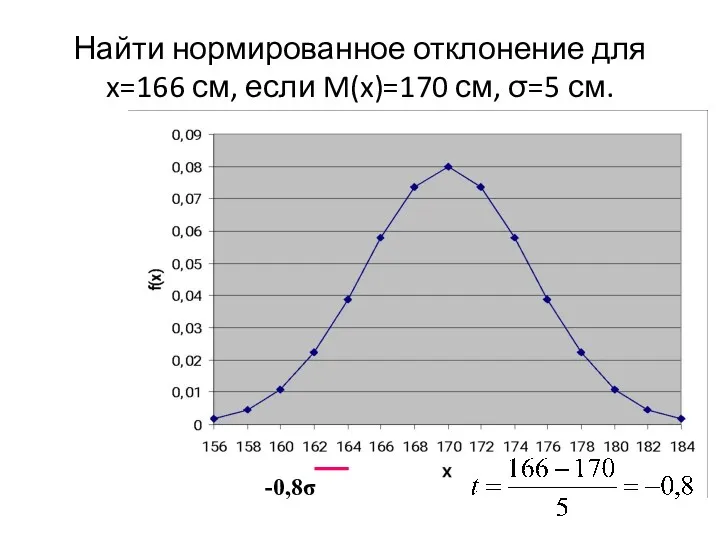
- 47. Найти нормированное отклонение для x=166 см, если M(x)=170 см, σ=5 см. -0,8σ
- 48. Вероятность попадания значения случайной величины в интервал от -∞ до x: Функция F(x) не выражается через
- 49. Вероятность попадания значения случайной величины в интервал от а до b: причем Ф(–t) = 1– Ф(t)
- 50. Задача: Найти вероятность попадания случайной величины в интервал от 155 см до 160 см если M(x)=a=170
- 51. Интервальные оценки нормированное отклонение х – μ=σt 1σ – 68,3%; 2σ – 95,5%; 3σ – 99,7%
- 52. Сравнительная характеристика значение генеральной средней с доверительным интервалом
- 53. Сравнение теоретических и эмпирических распределений Нулевая гипотеза. Согласно этой гипотезе первоначально принимается, что между эмпирическим и
- 54. Средние квадратические ошибки sА (асимметрии) и sЕ (эксцесса) Для достаточно большой выборки (n>30), если показатели асимметрии
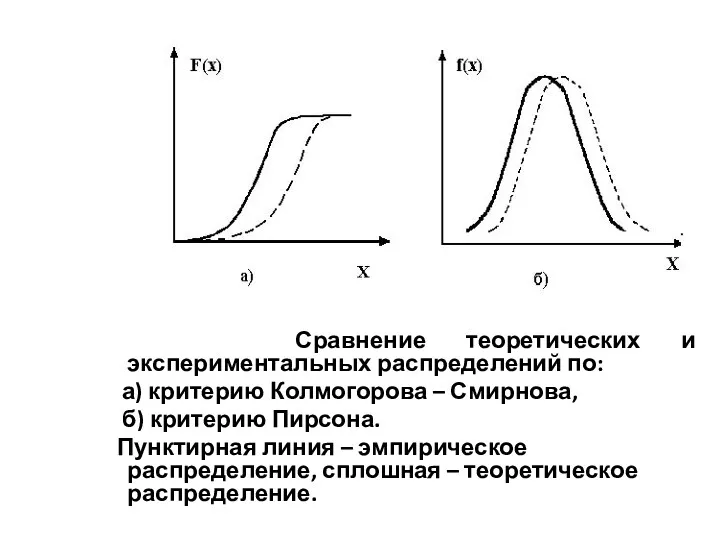
- 55. Сравнение теоретических и экспериментальных распределений по: а) критерию Колмогорова – Смирнова, б) критерию Пирсона. Пунктирная линия
- 56. Критерий Пирсона где mi – экспериментальные частоты попадания значения случайной величины в интервал, npi – теоретические
- 57. Число степеней свободы – это общее число величин, по которым вычисляются соответствующие статистические показатели, минус число
- 58. Заключение Нами рассмотрены: Основные параметры нормального распределения; Понятие доверительной вероятности и доверительного интервала; Нулевая гипотеза и
- 60. Скачать презентацию











































 Длина окружности. Площадь круга
Длина окружности. Площадь круга Числа от 1 до 9.
Числа от 1 до 9. Использование технологий, методов и приёмов интегрированных уроков для познавательной активности на уроках математики
Использование технологий, методов и приёмов интегрированных уроков для познавательной активности на уроках математики Показательные неравенства
Показательные неравенства Скобки в числовом выражении
Скобки в числовом выражении Понятие логарифма, основные свойства логарифмов
Понятие логарифма, основные свойства логарифмов Задачи на кратное сравнение
Задачи на кратное сравнение 20231011_8_klass_pryamougolnik._ploshchad_pryamougolnika
20231011_8_klass_pryamougolnik._ploshchad_pryamougolnika Геометрические фигуры
Геометрические фигуры Занимательная математика
Занимательная математика Великие математики и их открытия
Великие математики и их открытия Решение задач на нахождение площади фигур по готовым чертежам
Решение задач на нахождение площади фигур по готовым чертежам Сравнение дробей. Урок изучения нового материала в 5 классе
Сравнение дробей. Урок изучения нового материала в 5 классе Сложение рациональных чисел
Сложение рациональных чисел Родительское собрание №1. 2021-2022 учебный год
Родительское собрание №1. 2021-2022 учебный год Листая страницы истории (конференция)
Листая страницы истории (конференция) Практикум № 7 по решению стереометрических задач
Практикум № 7 по решению стереометрических задач Тела вращения. 11 класс
Тела вращения. 11 класс Цилиндр. Конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка
Цилиндр. Конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка Пропорция. Урок математики в 6 классе
Пропорция. Урок математики в 6 классе Открытый урок по математике. Тема:Задача.1 класс. Школа 2100
Открытый урок по математике. Тема:Задача.1 класс. Школа 2100 мастер класс по ФЭМП на тему: Обучению решению арифметических задач.
мастер класс по ФЭМП на тему: Обучению решению арифметических задач. Совместные действия с десятичными дробями. 6 класс
Совместные действия с десятичными дробями. 6 класс Комбинаторные методы обработки информации
Комбинаторные методы обработки информации Презентация к уроку математикиАрифметические действия над числами урок 32 программа Школа 2100
Презентация к уроку математикиАрифметические действия над числами урок 32 программа Школа 2100 Письменное умножение на двузначное число
Письменное умножение на двузначное число Метод дерева решений
Метод дерева решений