Содержание
- 2. Трудности решения геометрических задач Неалгоритмичность задач Необходимость выбора метода решения задачи и теоремы для решения конкретной
- 3. Необходимые условия успеха при решении задач по геометрии Уверенное владение основными понятиями и их свойствами (определения,
- 4. Причины ошибок в решении геометрических задач Незнание и/или непонимание аксиом, определений, теорем Неумение их применять Невнимательное
- 5. Специфические особенности методов решения геометрических задач Большое разнообразие Взаимозаменяемость Трудность формального описания Отсутствие чётких границ применения
- 6. Некоторые методы решения геометрических задач второй части ОГЭ Применение ключевых задач Метод вспомогательных построений Переход к
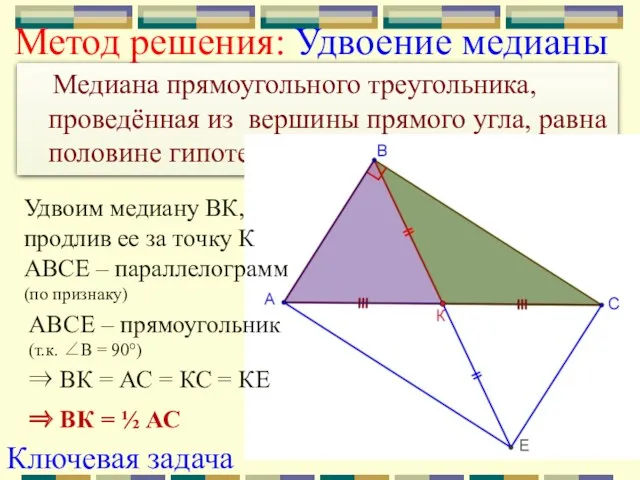
- 7. Метод решения: Удвоение медианы Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. АВСЕ
- 8. Следствие из свойства медианы к гипотенузе. Ключевая задача Медиана прямоугольного треугольника, проведённая к гипотенузе, делит треугольник
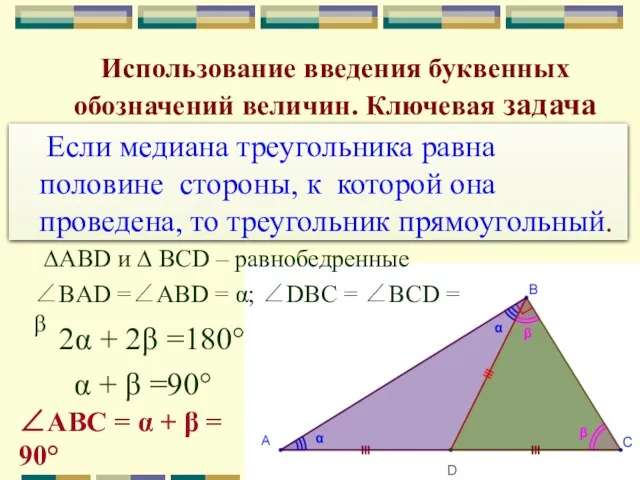
- 9. Использование введения буквенных обозначений величин. Ключевая задача Если медиана треугольника равна половине стороны, к которой она
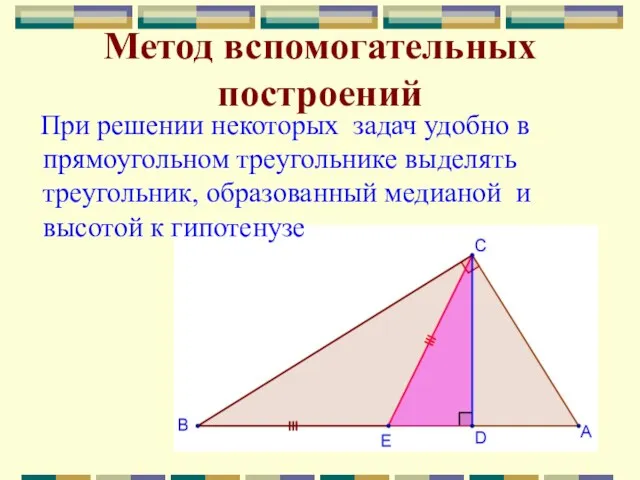
- 10. Метод вспомогательных построений При решении некоторых задач удобно в прямоугольном треугольнике выделять треугольник, образованный медианой и
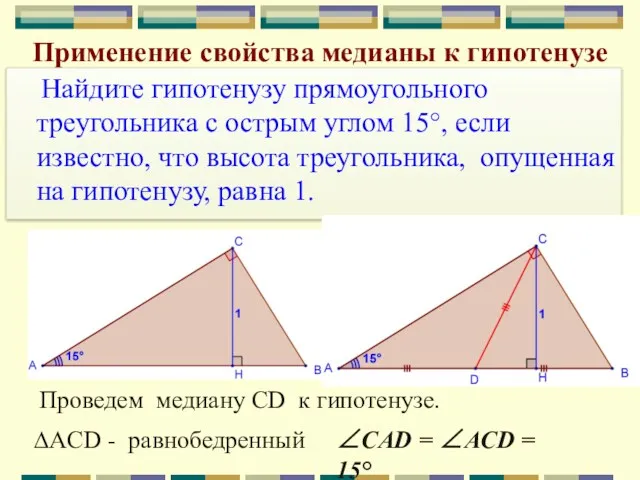
- 11. Применение свойства медианы к гипотенузе Найдите гипотенузу прямоугольного треугольника с острым углом 15°, если известно, что
- 12. Найдите гипотенузу прямоугольного треугольника с острым углом 15°, если известно, что высота треугольника, опущенная на гипотенузу,
- 13. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18. СD =
- 14. Свойства площади треугольника Площади треугольников, имеющих общую высоту (равные высоты) , относятся как стороны, к которым
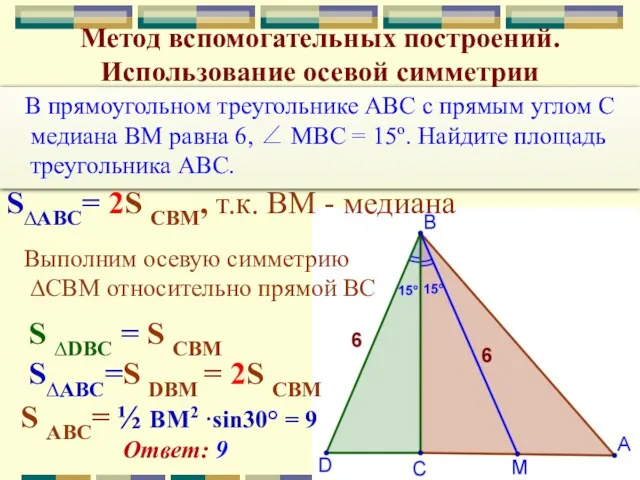
- 15. Метод вспомогательных построений. Использование осевой симметрии В прямоугольном треугольнике ABC c прямым углом С медиана BM
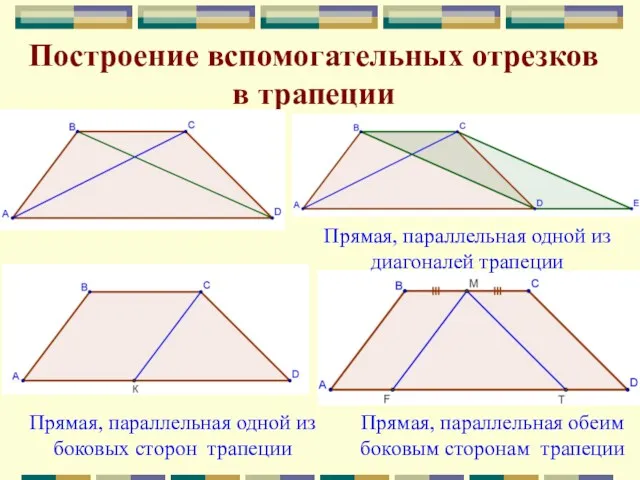
- 16. Построение вспомогательных отрезков в трапеции Прямая, параллельная одной из диагоналей трапеции Прямая, параллельная одной из боковых
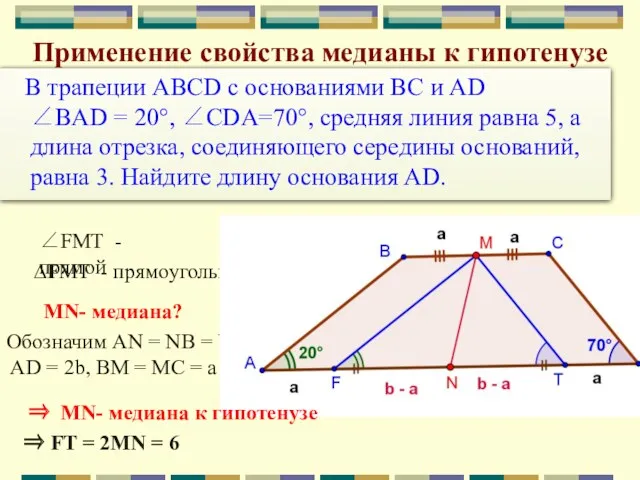
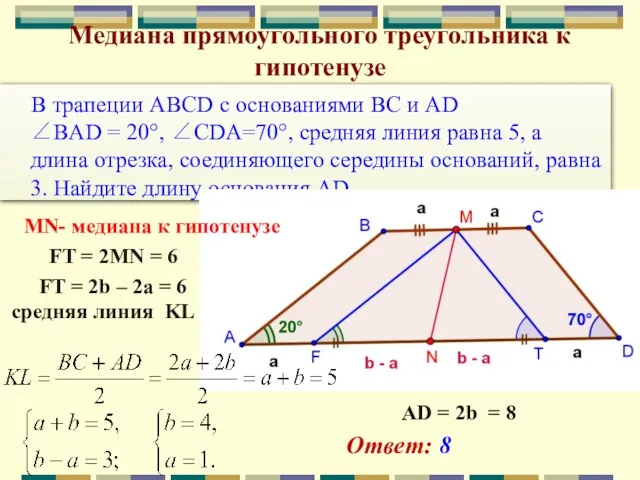
- 17. В трапеции ABCD с основаниями BC и AD ∠BAD = 20°, ∠CDA=70°, средняя линия равна 5,
- 18. В трапеции ABCD с основаниями BC и AD ∠BAD = 20°, ∠CDA=70°, средняя линия равна 5,
- 19. В трапеции ABCD с основаниями BC и AD ∠BAD = 20°, ∠CDA=70°, средняя линия равна 5,
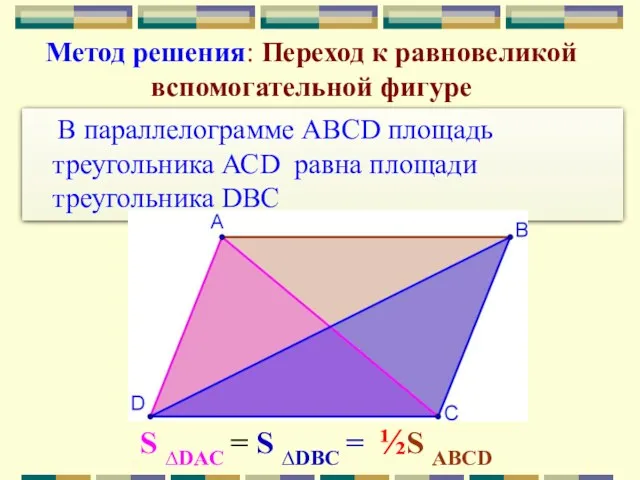
- 20. В параллелограмме ABCD площадь треугольника АСD равна площади треугольника DBС Метод решения: Переход к равновеликой вспомогательной
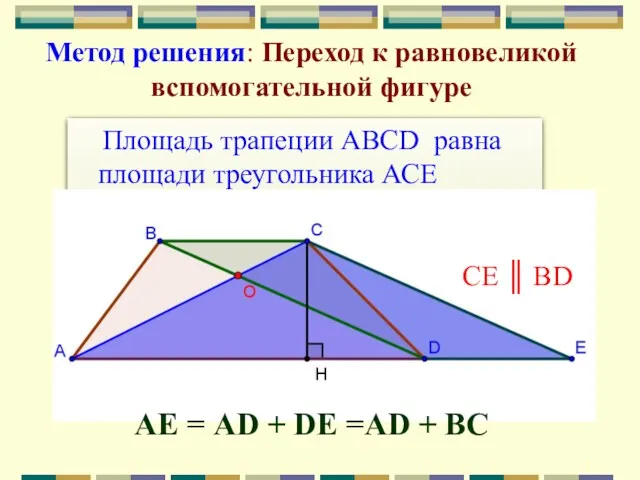
- 21. Площадь трапеции АВСD равна площади треугольника АСЕ Метод решения: Переход к равновеликой вспомогательной фигуре АЕ =
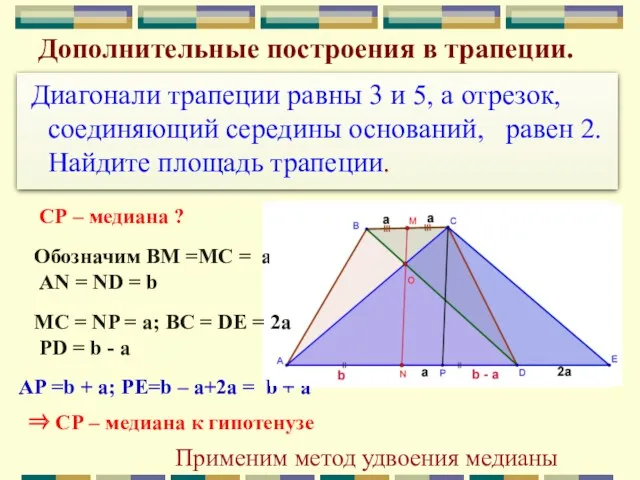
- 22. Дополнительные построения в трапеции. Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен
- 23. Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
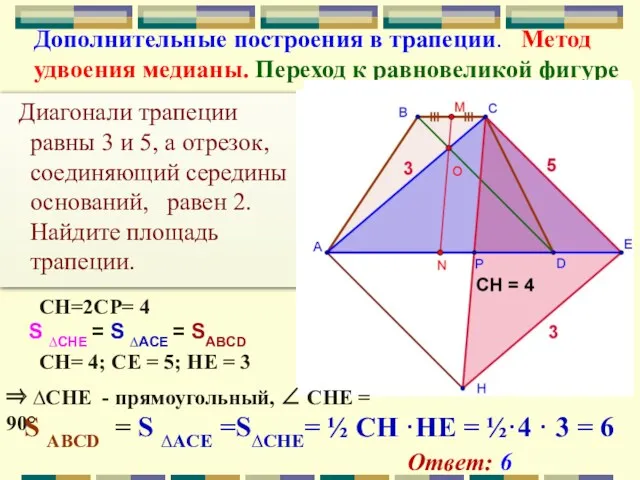
- 24. Дополнительные построения в трапеции. Метод удвоения медианы. Переход к равновеликой фигуре Диагонали трапеции равны 3 и
- 25. Метод площадей Идея метода: площади фигуры находим, используя различные формулы или различные отрезки и углы. Приравняв
- 26. Медиана BM треугольника ABC равна его высоте AH. Найдите угол MBC. Метод площадей Пусть ∠МВС =
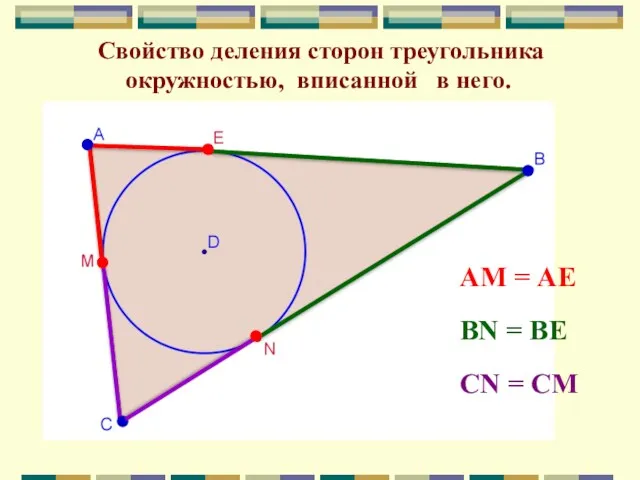
- 27. Свойство деления сторон треугольника окружностью, вписанной в него. АМ = АЕ BN = BЕ CN =
- 28. В треугольник вписана окружность радиуса 4. Одна из сторон треугольника разделена точкой касания на части, равные
- 29. Метод решения: Введение вспомогательной окружности Идея метода: ввести в рассмотрение окружность, если это возможно в данной
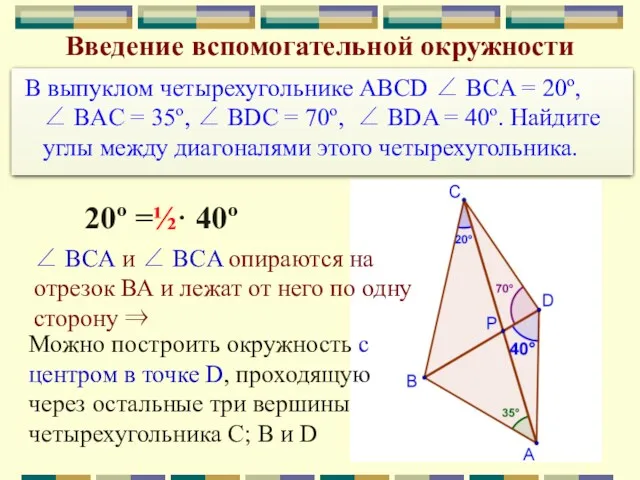
- 30. Введение вспомогательной окружности В выпуклом четырехугольнике ABCD ∠ BCA = 20º, ∠ BAC = 35º, ∠
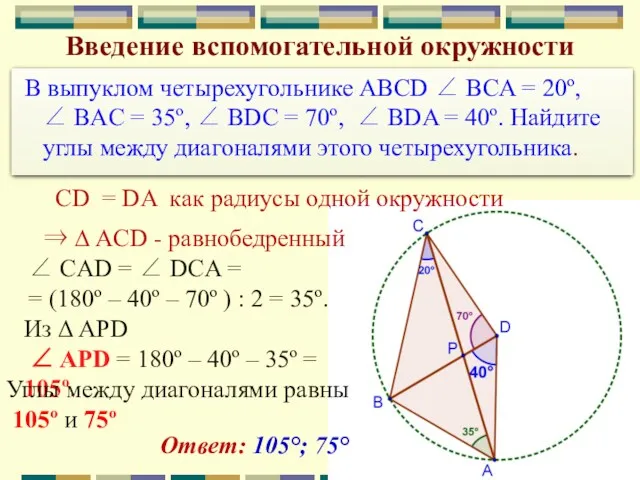
- 31. Введение вспомогательной окружности ∠ СAD = ∠ DСA = = (180º – 40º – 70º )
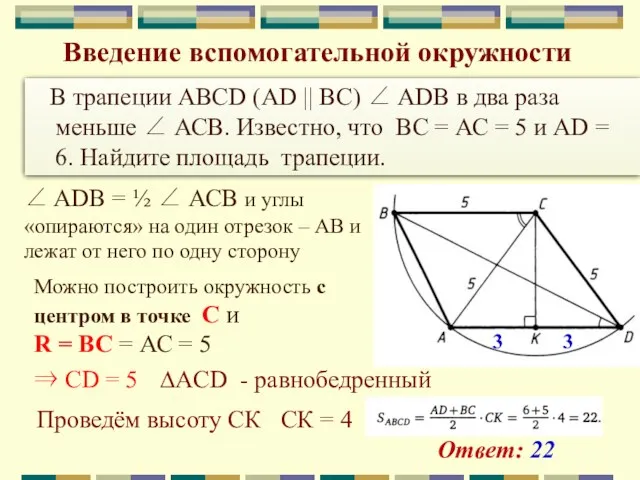
- 32. Введение вспомогательной окружности В трапеции ABCD (AD || ВС) ∠ ADB в два раза меньше ∠
- 33. Рекомендации учащимся при решении геометрических задач
- 34. О чертеже Хороший чертеж – помощник Все, что «увидено», должно быть обосновано Соблюдай пропорции и соотношения
- 35. О поиске решения задачи Треугольник равнобедренный, следовательно … Две касательные проведены из одной точки, следовательно …
- 37. Скачать презентацию


















 Подготовка к контрольной работе Умножение и деление дробей
Подготовка к контрольной работе Умножение и деление дробей Моделирование систем. Классификация моделей
Моделирование систем. Классификация моделей Віднімання двоцифрових чисел. Задача на находження невідомого зменшуваного. Визначення часу. Урок №125
Віднімання двоцифрових чисел. Задача на находження невідомого зменшуваного. Визначення часу. Урок №125 тест по математике для 2 класса
тест по математике для 2 класса Современный урок математики в свете ФГОС
Современный урок математики в свете ФГОС Знакомство с числами 2-го десятка. Состав чисел
Знакомство с числами 2-го десятка. Состав чисел Открытый урок математика 3 класс.
Открытый урок математика 3 класс. Изучение таблицы умножения
Изучение таблицы умножения Презентация по математике: Таблица умножения и деления на 8 и 9
Презентация по математике: Таблица умножения и деления на 8 и 9 Дидактическое пособие Математический театр
Дидактическое пособие Математический театр Математические и структурные модели управления
Математические и структурные модели управления Открытое занятие по ФЭМП в старшей группе детского сада
Открытое занятие по ФЭМП в старшей группе детского сада Золотое сечение
Золотое сечение Шифры и математика
Шифры и математика Тренажер Сложение и вычитание с переходом через разряд 2 класс
Тренажер Сложение и вычитание с переходом через разряд 2 класс Площади фигур. Теорема Пифагора
Площади фигур. Теорема Пифагора Программа Живая геометрия
Программа Живая геометрия Графики функций с модулями. 10 класс
Графики функций с модулями. 10 класс Решение задач по теме Параллельные прямые
Решение задач по теме Параллельные прямые Окружность в планиметрических задачах повышенного уровня ОГЭ и ЕГЭ
Окружность в планиметрических задачах повышенного уровня ОГЭ и ЕГЭ График функции
График функции Деление с остатком
Деление с остатком Презентация к мастер-классу Системно-деятельностный подход при решении задач
Презентация к мастер-классу Системно-деятельностный подход при решении задач Компоненты вычитания
Компоненты вычитания Математика и спорт
Математика и спорт Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива.
Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива. Смежные и вертикальные углы, их свойства
Смежные и вертикальные углы, их свойства Контроль качества продукции. Статистический контроль качества
Контроль качества продукции. Статистический контроль качества