Отношения следования и равносильности презентация

Импликацией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)⇒В(х), заданный на том же множестве, который ложен лишь при тех значениях х ∈ Х, при которых А(х) истинен, а В(х) ложен.

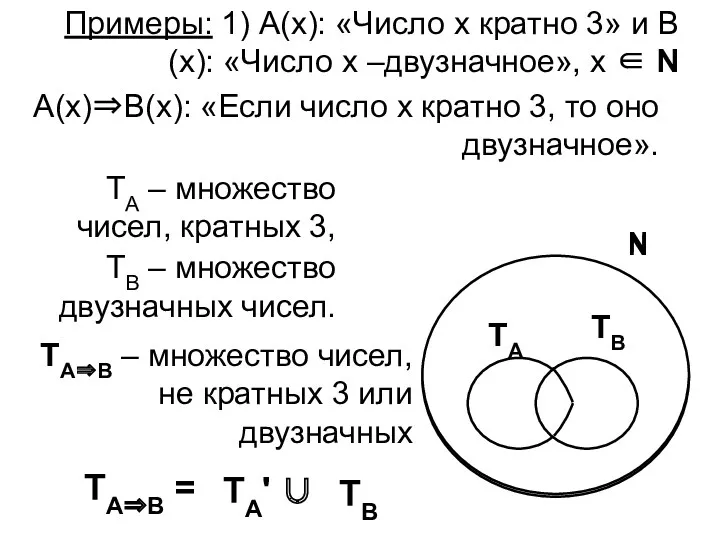
Примеры: 1) А(х): «Число х кратно 3» и В(х): «Число х –двузначное», х ∈ N
А(х)⇒В(х): «Если число х кратно 3, то оно двузначное».
ТА – множество чисел, кратных 3,
ТВ – множество двузначных чисел.
ТА⇒В – множество чисел, не кратных 3 или двузначных
ТА⇒В =
ТА'
∪
ТВ

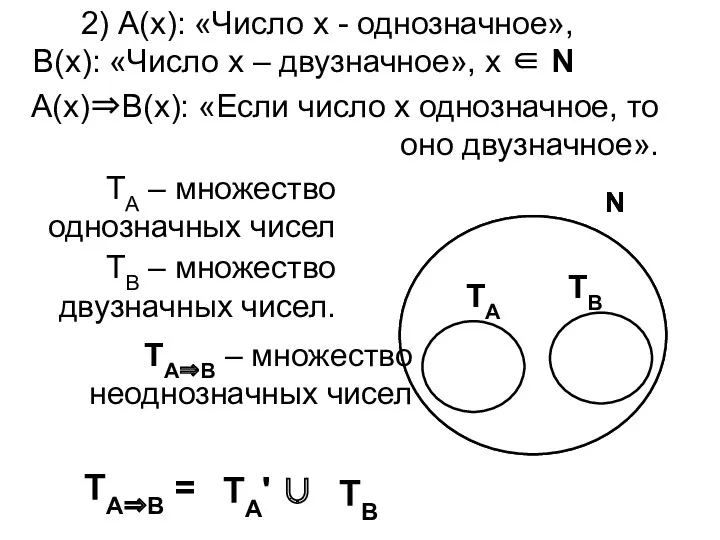
2) А(х): «Число х - однозначное», В(х): «Число х – двузначное», х ∈ N
А(х)⇒В(х): «Если число х однозначное, то оно двузначное».
ТА – множество однозначных чисел
ТВ – множество двузначных чисел.
ТА⇒В – множество неоднозначных чисел

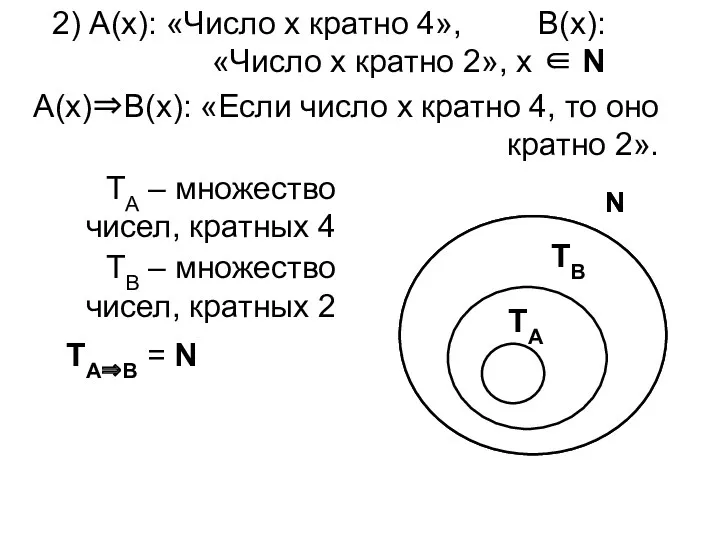
2) А(х): «Число х кратно 4», В(х): «Число х кратно 2», х ∈ N
А(х)⇒В(х): «Если число х кратно 4, то оно кратно 2».
ТА – множество чисел, кратных 4
ТВ – множество чисел, кратных 2
ТА⇒В = N

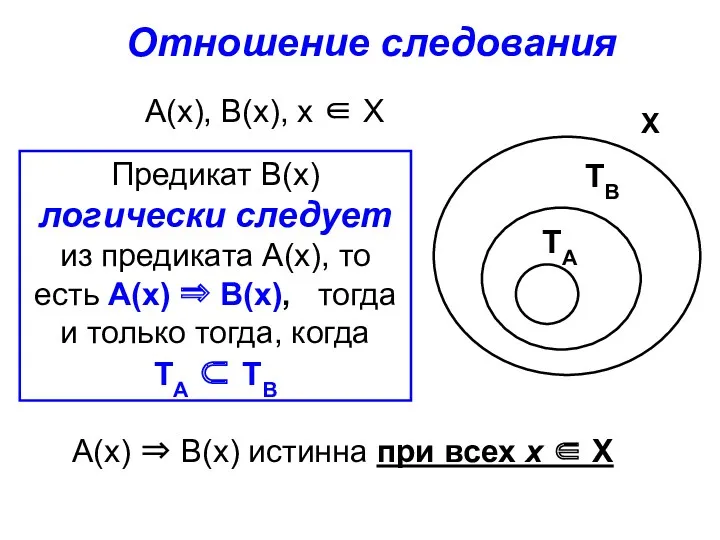
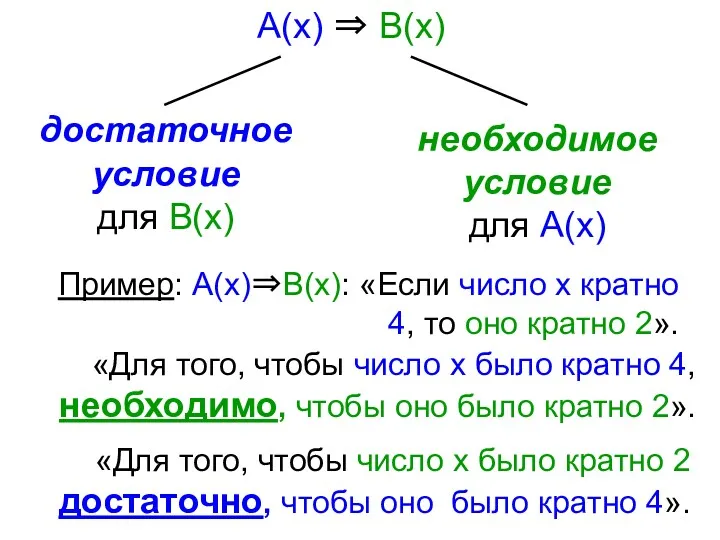
Отношение следования
А(х), В(х), х ∈ Х
А(х) ⇒ В(х) истинна при всех х ∈ Х
Предикат В(х) логически следует из предиката А(х), то есть А(х) ⇒ В(х), тогда и только тогда, когда ТА ⊂ ТВ

Пример: А(х)⇒В(х): «Если число х кратно 4, то оно кратно 2».
«Для того, чтобы число х было кратно 4, необходимо, чтобы оно было кратно 2».
«Для того, чтобы число х было кратно 2 достаточно, чтобы оно было кратно 4».

Эквиваленцией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)⇔В(х), заданный на том же множестве, который истинен лишь при тех значениях х ∈ Х, при которых оба предиката истинны или оба ложны.

Если предикаты А(х) и В(х) равносильны на множестве Х, то эквиваленция предикатов А(х) ⇔ В(х) истинна при всех х ∈Х.
Отношение равносильности
Предикаты А(х) и В(х) равносильны, то есть А(х) ⇔ В(х), тогда и только тогда, когда ТА = ТВ
Пусть даны предикаты А(х) и В(х), х ∈Х.

Пример: А(х) «Число х делится на 10»,
В(х): «Запись числа х заканчивается цифрой 0»
А(х)⇔В(х): «Число х делится на 10 тогда и только тогда, когда его запись оканчивается 0»
ТА – множество чисел, кратных 10,
ТВ – множество чисел, запись которых оканчивается цифрой 0.
ТА = ТВ, значит А(х) ⇔ В(х),
то есть эквиваленция А(х) ⇔ В(х) истинна при всех х ∈ N

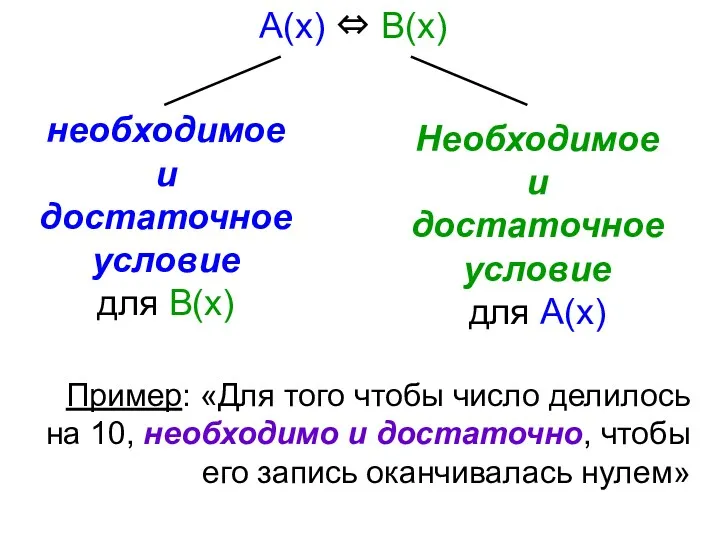
Пример: «Для того чтобы число делилось на 10, необходимо и достаточно, чтобы его запись оканчивалась нулем»

Замечание. Из равносильности предикатов А(х) и В(х) на некотором множестве Х не следует, что предикаты, выраженные теми же словами, окажутся равносильными на другом множестве Y.
Пример:
А(х): «Все стороны четырехугольника равны»,
В(х): «Диагонали четырехугольника перпендикулярны».

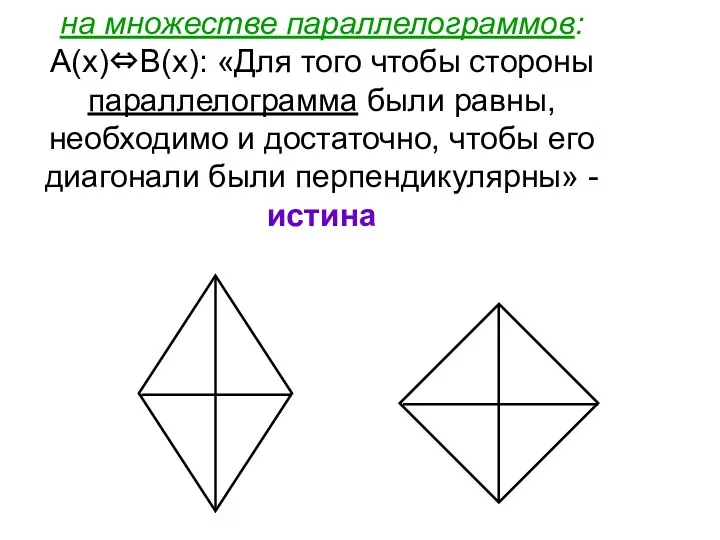
на множестве параллелограммов:
А(х)⇔В(х): «Для того чтобы стороны параллелограмма были равны, необходимо и достаточно, чтобы его диагонали были перпендикулярны» - истина

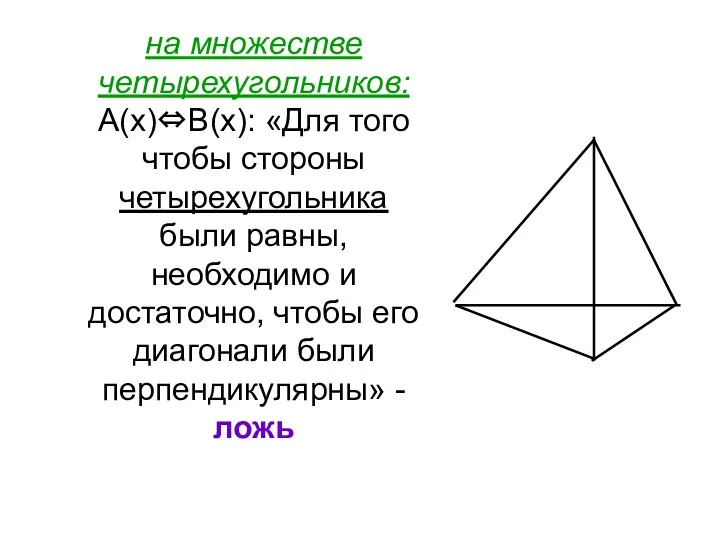
на множестве четырехугольников:
А(х)⇔В(х): «Для того чтобы стороны четырехугольника были равны, необходимо и достаточно, чтобы его диагонали были перпендикулярны» - ложь

Теоремы

Теорема – это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).
Теорема - от греч. τεορεμα - представление, зрелище

С логической точки зрения теорема представляет собой высказывание А(х) ⇒ В(х), где А(х) и В(х) – предикаты, причем В(х) логически следует из А(х), то есть В(х) обращается в истинное высказывание при всех тех значениях х, при которых А(х) истинен.
А(х) – условие теоремы, В(х) – заключение теоремы.
Теорема может быть сформулирована с помощью слов «если …, то…», «следует», «необходимо», «достаточно», а также без использования этих слов.

Пример: «В прямоугольнике диагонали равны».
Если четырехугольник является прямоугольником, то диагонали в нем равны
Из того, что четырехугольник является прямоугольником следует, что его диагонали равны
Для того чтобы в четырехугольнике диагонали были равны, достаточно, чтобы он был прямоугольником
Для того чтобы четырехугольник был прямоугольником, необходимо, чтобы его диагонали были равны

Кроме условия и заключения теорема содержит разъяснительную часть (словесно она обычно не формулируется, но всегда подразумевается, и при работе с теоремой ее необходимо выделять).
В рассмотренном выше примере разъяснительная часть следующая: работаем на множестве всех прямоугольников.

В математике кроме теорем используются предложения, называемые правилами и формулами.
Пример: правило деления суммы на число:
«для того, чтобы разделить сумму на число, можно разделить на это число каждое из слагаемых и полученные результаты сложить»
(а + b) : с = а : с + b : с
Условие: а, b и с – целые неотрицательные числа (с ≠ 0), а  с и b  с
Заключение: (а + b) : с = а : с + b : с

А(х) ⇒ В(х) – данная теорема
В(х) ⇒ А(х)
- теорема обратная данной
- теорема противоположная данной
теорема обратная противоположной или
противоположная обратной

А(х) ⇒ В(х): «Если сумма цифр числа кратна 9, то и само число кратно 9»
В(х) ⇒ А(х):
«Если число кратно 9, то и сумма цифр числа кратна 9»
: «Если сумма цифр числа не кратна 9, то и число не кратно 9»
: «Если число не кратно 9, то и сумма цифр числа не кратна 9»

Замечание. Если условие или заключение данной теоремы представляет собой конъюнкцию или дизъюнкцию, то чтобы получить теорему противоположную данной и обратную противоположной (противоположную обратной), нужно учитывать правила построения отрицания конъюнкции или дизъюнкции.

ПРИМЕР:
А(х) ⇒ В(х): «ЕСЛИ ЧИСЛО ДЕЛИТСЯ НА 3 И НА 5, ТО ОНО ДЕЛИТСЯ НА 15»
: «Если число не делится на 3 или не делится на 5, то оно не делится на 15»
: «Если число не делится на 15, то оно не делится на 3 или не делится на 5»

Если для данной теоремы А(х) ⇒ В(х) истинна обратная теорема В(х) ⇒ А(х), то их можно объединить в одну А(х) ⇔ В(х), и тогда в формулировке будут использоваться слова «необходимо и достаточно»,
«тогда и только тогда, когда»

Пример:
А(х) ⇒ В(х): «В равнобедренном треугольнике углы при основании равны»
В(х) ⇒ А(х):
«Если в треугольнике углы при основании равны, то треугольник равнобедренный»

А(х) ⇔ В(х): «Для того, чтобы треугольник был равнобедренным, необходимо и достаточно, чтобы в нем углы при основании были равны»
или
«Треугольник будет равнобедренным тогда и только тогда, когда в нем углы при основании будут равны»

ЕСЛИ ТЕОРЕМА ИМЕЕТ ВИД РАВНОСИЛЬНОСТИ А(Х) ⇔ В(Х), ТО ЭТО ЗНАЧИТ, ЧТО ОНА СОСТОИТ ИЗ ДВУХ ВЗАИМНО ОБРАТНЫХ ТЕОРЕМ:
А(Х) ⇒ В(Х) И В(Х) ⇒ А(Х),
И, СЛЕДОВАТЕЛЬНО, ЕЕ ДОКАЗАТЕЛЬСТВО СВОДИТСЯ К ДОКАЗАТЕЛЬСТВУ ДВУХ УКАЗАННЫХ ТЕОРЕМ

Упражнения:
Выделите условие и заключение в каждой из следующих теорем:
а) Диагонали прямоугольника равны.
б) Равенство треугольников есть достаточное условие их равновеликости.
2. Для данной теоремы сформулируйте обратную, противоположную и обратную противоположной теоремы : «Диагонали ромба взаимно перпендикулярны».
3. Покажите, что следующая теорема является объединением двух теорем: «На 5 делятся те и только те числа, запись которых оканчивается цифрой 0 или цифрой 5»