Содержание
- 2. Предполагаем, что . Ln(x) — многочлен Лагранжа: для всех i=0,...,n [a,b] — отрезок, содержащий узлы x0,
- 3. Запишем равенство где – многочлен определённый через узлы x0, x1, ..., xn и С – некоторая
- 4. Введём в рассмотрение функцию 03.10.2014 13:29
- 5. Итак, существует : . Так как и получаем Отсюда 03.10.2014 13:29
- 6. Для остаточного члена получаем выражение 03.10.2014 13:29
- 7. Точное представление f(x) через её интерполяционный многочлен Лагранжа : где и зависит от x. Можно оценить
- 8. Пример. Оценить с какой точностью можно вычислить по формуле Лагранжа , если известны значения 03.10.2014 13:29
- 9. Улучшение (уменьшение погрешности) интерполирования за счёт выбора узлов. 03.10.2014 13:29 Задача. Дана функция на отрезке ,
- 10. Многочлен Чебышева 03.10.2014 13:29
- 11. 03.10.2014 13:29 Обозначим
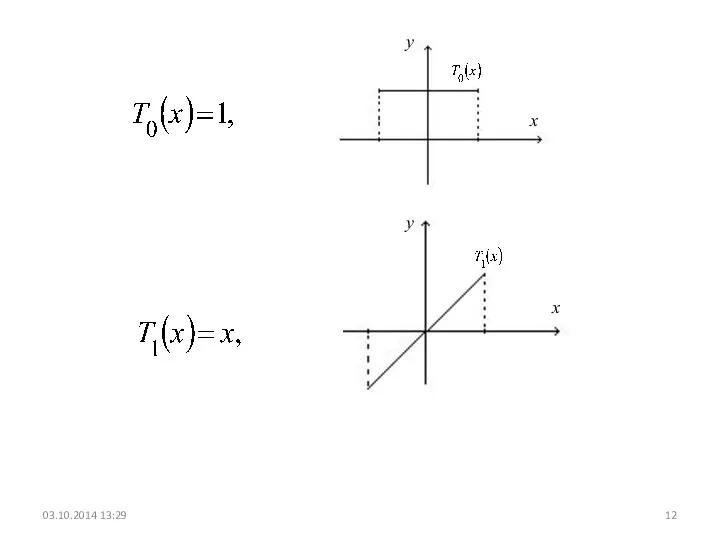
- 12. 03.10.2014 13:29 x y y x
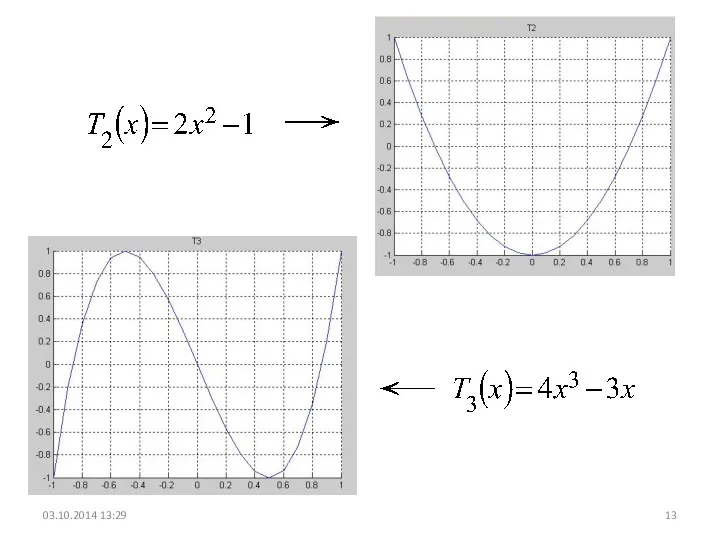
- 13. 03.10.2014 13:29
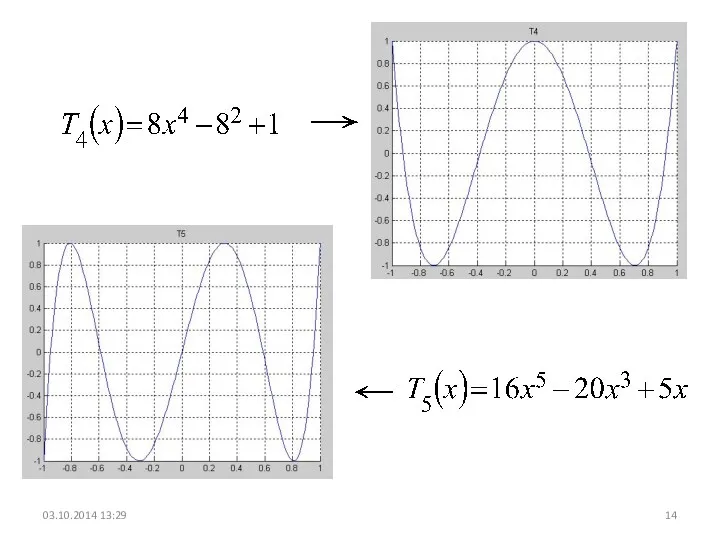
- 14. 03.10.2014 13:29
- 15. 03.10.2014 13:29
- 16. 03.10.2014 13:29 Замечание. Корни расположены неравномерно и сгущаются к концам отрезка
- 17. 03.10.2014 13:29 Теорема Чебышева. Из всех полиномов n-й степени со старшим коэффициентом равным 1, у полинома
- 18. 03.10.2014 13:29 Теорема. Корни многочлена минимизируют в оценке погрешности интерполяционного многочлена. При этом и Тогда
- 19. 03.10.2014 13:29 При интерполировании на произвольном отрезке линейной заменой функция переводится на отрезок Рассматривается функция при
- 21. Скачать презентацию










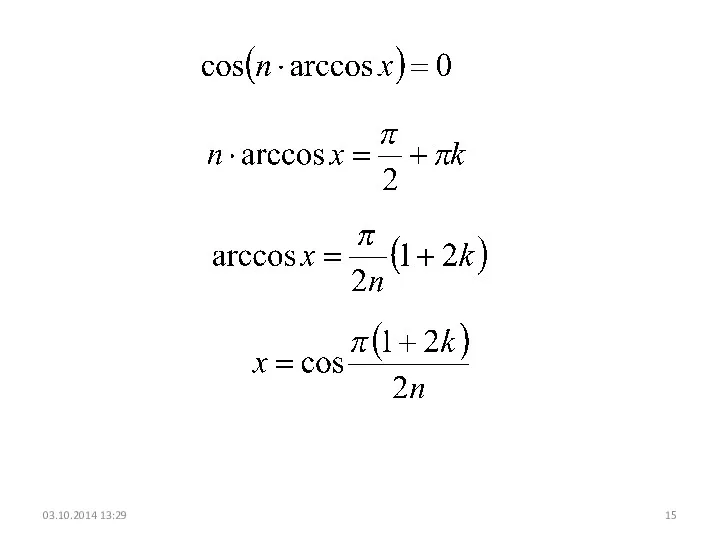




 Методы решения текстовых задач
Методы решения текстовых задач Устные задачи на готовых чертежах. Смежные и вертикальные углы
Устные задачи на готовых чертежах. Смежные и вертикальные углы Формулы сокращенного умножения. Путешествие По стране формул
Формулы сокращенного умножения. Путешествие По стране формул Комбинаторика. Теория вероятности
Комбинаторика. Теория вероятности Умножение десятичных дробей. Тренажер
Умножение десятичных дробей. Тренажер Mixed strategy Nash equilibrium. (Lecture 3)
Mixed strategy Nash equilibrium. (Lecture 3) Относительная частота случайного события. Интегрированный урок в 9 классе математика + английский язык
Относительная частота случайного события. Интегрированный урок в 9 классе математика + английский язык Сложение и вычитание чисел
Сложение и вычитание чисел Математические модели и математическое моделирование
Математические модели и математическое моделирование Свойства производной. Построение графиков функций
Свойства производной. Построение графиков функций Квадратный трехчлен. 8 класс
Квадратный трехчлен. 8 класс Ықтималдықтар теориясының негіздері
Ықтималдықтар теориясының негіздері Математический брейн-ринг для учащихся 5 класса
Математический брейн-ринг для учащихся 5 класса Конспект урока математики в 3 классе Истомина
Конспект урока математики в 3 классе Истомина Осевая и центральная симметрии
Осевая и центральная симметрии Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Решение рациональных уравнений
Решение рациональных уравнений Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Весёлый счёт.
Весёлый счёт. Дидактическая игра по ФЭМП Помоги Буратино достать ключик (подготовительная группа).
Дидактическая игра по ФЭМП Помоги Буратино достать ключик (подготовительная группа). Дисперсионный анализ ANOVA (продолжение). Занятие 4
Дисперсионный анализ ANOVA (продолжение). Занятие 4 Метрология — наука об измерениях, методах и средствах обеспечения их единства
Метрология — наука об измерениях, методах и средствах обеспечения их единства Додавання і віднімання числа частинами
Додавання і віднімання числа частинами Метрология. Научные изыскания в области метрологии
Метрология. Научные изыскания в области метрологии Пропорции
Пропорции Степень с рациональным показателем. Степенная функция
Степень с рациональным показателем. Степенная функция Дополнительные возможности анализа данных в MS Excel. Аппроксимация экспериментальных данных. Линии тренда
Дополнительные возможности анализа данных в MS Excel. Аппроксимация экспериментальных данных. Линии тренда Решение задач с помощью дробных рациональных уравнений
Решение задач с помощью дробных рациональных уравнений