Содержание
- 2. Концентрация внимания Концентрация внимания равна N. N = (число верно указанных чисел) x 0,125 x 100%
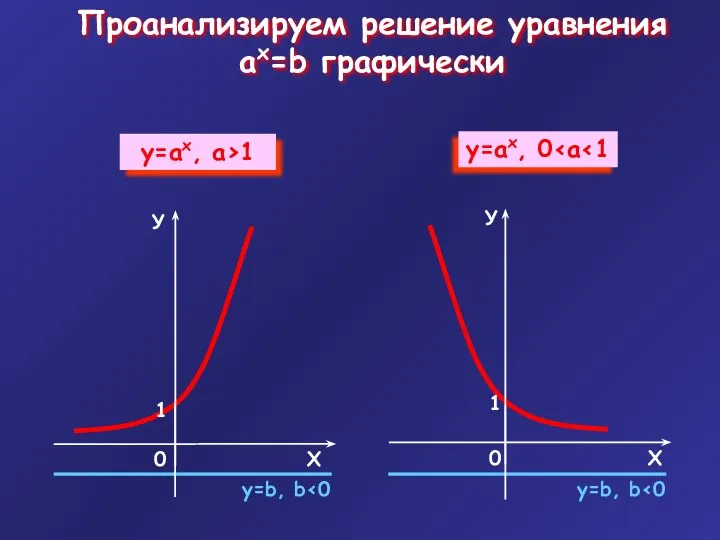
- 4. Проанализируем решение уравнения ax=b графически у=b, b у=b, b
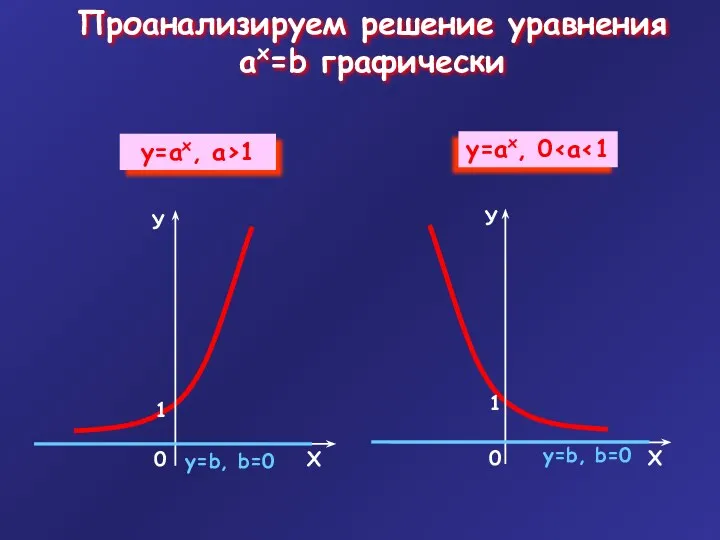
- 5. Проанализируем решение уравнения ax=b графически у=b, b=0 у=b, b=0
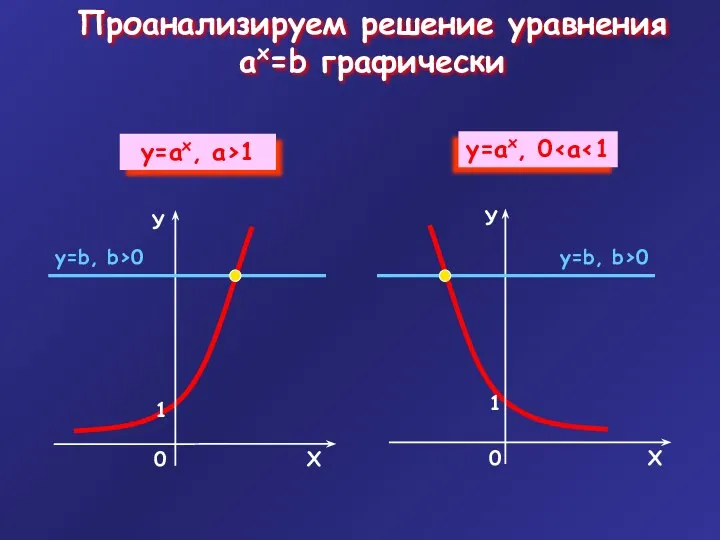
- 6. Проанализируем решение уравнения ax=b графически у=b, b>0 у=b, b>0
- 7. Уравнение ax=b корней не имеет Уравнение ax=b имеет единственное решение x=logab b>0 b≤0 Вывод:
- 8. Пример:
- 9. Во многих случаях решение показательных уравнений после надлежащих преобразований сводится к решению простейших показательных уравнений. При
- 10. ОТВЕТ: -5 ; 1.
- 11. ОТВЕТ: 1.
- 13. ПРИМЕР Показательные уравнения, сводящиеся к квадратным уравнениям. ТИП Вернемся к переменной Х . ОТВЕТ:
- 15. ОТВЕТ:
- 17. . Вернёмся к переменной x ОТВЕТ: 0 ; 1
- 18. Вернёмся к переменной x ОТВЕТ: 0 ; 1.
- 20. ОТВЕТ: Вернёмся к переменной x
- 22. Введём функции и . Функция убывает на R, как сумма убывающих на R. Функция постоянна на
- 23. Легко определить и проверить, что х=3 - корень данного уравнения. Покажем, что других корней уравнение иметь
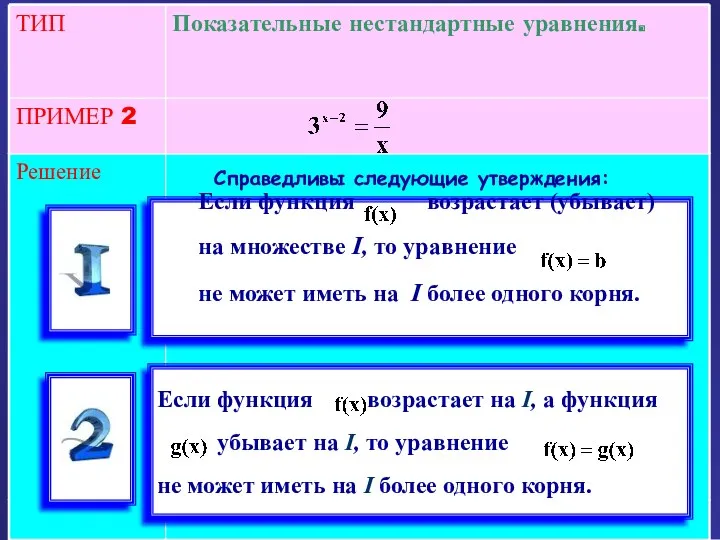
- 24. Решение ПРИМЕР 2 Показательные нестандартные уравнения. ТИП Справедливы следующие утверждения: Если функция возрастает (убывает) на множестве
- 25. ОТВЕТ: 3 Введём функции и . Показательная функция ( ) возрастает на R. Функция (обратная пропорциональность)
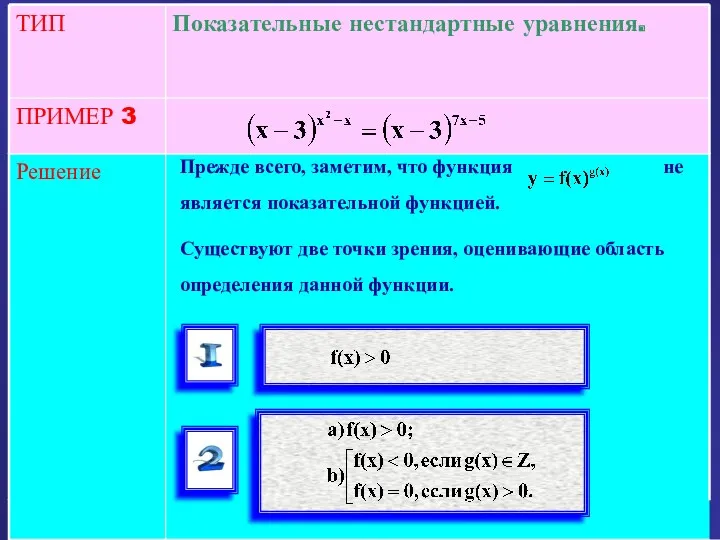
- 26. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Прежде всего, заметим, что функция не является показательной функцией.
- 27. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Решим данное уравнение, придерживаясь второй точки зрения. Вначале проверим,
- 28. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Проверка показала, что x=3 является корнем уравнения. Проверка показала,
- 29. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Теперь установим, какие из корней уравнения удовлетворяют исходному уравнению.
- 30. ОТВЕТ: 5 ; 4 ; 3 ; 1 Проверка показала, что х=5 является корнем уравнения. Замечание:
- 31. Домашнее задание:
- 33. Скачать презентацию

























 Решение задач на концентрацию, смеси и сплавы
Решение задач на концентрацию, смеси и сплавы Уравнение. Задание В5, ЕГЭ
Уравнение. Задание В5, ЕГЭ Викторина для 5 - 6 классов
Викторина для 5 - 6 классов Математическое описание случайных явлений
Математическое описание случайных явлений Исследование основных характеристик случайных процессов
Исследование основных характеристик случайных процессов Піраміда. Правильна піраміда. (Геометрія 11 клас)
Піраміда. Правильна піраміда. (Геометрія 11 клас) Логарифмические неравенства. (11 класс)
Логарифмические неравенства. (11 класс) Задачи на дроби
Задачи на дроби Преобразование выражений при решений уравнений
Преобразование выражений при решений уравнений Числовые характеристики случайных величин. Математическое ожидание
Числовые характеристики случайных величин. Математическое ожидание Математика 3 класс Тема: Решение задач с применением изученных формул
Математика 3 класс Тема: Решение задач с применением изученных формул урок математики в 1 классе Числа 1 – 10 . Закрепление
урок математики в 1 классе Числа 1 – 10 . Закрепление Наибольшее и наименьшее значение функции
Наибольшее и наименьшее значение функции Прямоугольный треугольник и некоторые его свойства
Прямоугольный треугольник и некоторые его свойства Тест по теме: Теорема Пифагора
Тест по теме: Теорема Пифагора Деление на десятичную дробь
Деление на десятичную дробь Урок Объем шара и его частей
Урок Объем шара и его частей Выражения с переменной. УМК Школа 2100
Выражения с переменной. УМК Школа 2100 Выборки. Проблемы контроля в экспериментальных исследованиях
Выборки. Проблемы контроля в экспериментальных исследованиях Учение о дробях. Математики древнего Египта
Учение о дробях. Математики древнего Египта Статистика о вреде курения
Статистика о вреде курения Делители и кратные (часть 1)
Делители и кратные (часть 1) Теңдеулер мен теңсіздіктер. Бір айнымалысы бар теңдеулер. Мәндес теңдеулер
Теңдеулер мен теңсіздіктер. Бір айнымалысы бар теңдеулер. Мәндес теңдеулер Обратная матрица. (Тема 7)
Обратная матрица. (Тема 7) Непрерывность функции в точке и на отрезке
Непрерывность функции в точке и на отрезке Арифметическая и геометрическая последовательности
Арифметическая и геометрическая последовательности Своя игра по математике. 5 класс
Своя игра по математике. 5 класс Устный счет. 1 класс
Устный счет. 1 класс