Содержание
- 2. {уn}: 1,3,5,7,9,…,(2n-1),... Расходится Нет точки сгущения Нет предела {хn}: 1,1/2,1/3,1/4,1/5,…1/n,.. Сходится Точка сгущения-0 Предел последовательности-0 1.
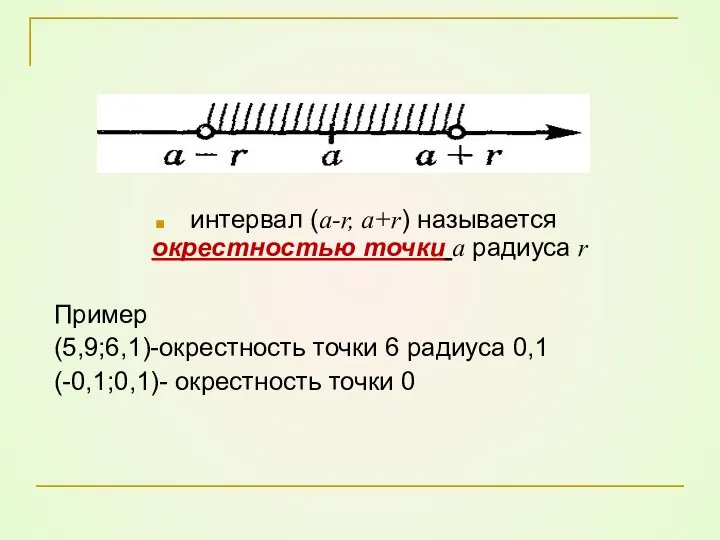
- 3. интервал (a-r, a+r) называется окрестностью точки a радиуса r Пример (5,9;6,1)-окрестность точки 6 радиуса 0,1 (-0,1;0,1)-
- 4. Число a∈ℝ называется пределом последовательности { xn } если ∀ε>0 ∃N∈ℕ такое, что | xn –
- 5. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ предела последовательности Пусть r∈ℝ, M(r)∈Ox M(r) – геометрическая интерпретация числа r∈ℝ . Пусть x0∈ℝ,
- 6. Вывод: (из определения предела последовательности) если {xn}→a , то с геометрической точки зрения это означает, что
- 7. Примеры
- 8. Свойства пределов последовательностей ● Последовательность может иметь только один предел ● Если последовательность сходится , то
- 9. Последовательность, предел которой равен нулю, называют бесконечно малой (б.м) ЛЕММА. Число a∈ℝ является пределом последовательности {xn}
- 10. Замечание * 1. Если {xn} и {yn} б.м последовательности, то сумма { xn+ yn }, разность{
- 11. Правила вычисления пределов 1) Предел суммы равен сумме пределов: 2) Предел произведения равен произведению пределов: Пусть
- 12. ДОКАЗАТЕЛЬСТВО Будем использовать лемму б. м. последовательности и замечание * Самостоятельно (аналогично) доказать правила 3 и
- 13. Теорема о «двух милиционерах» Пусть последовательности {xn} и {yn} сходятся к одному и тому же числу
- 14. Виды неопределённостей и способы их раскрытия
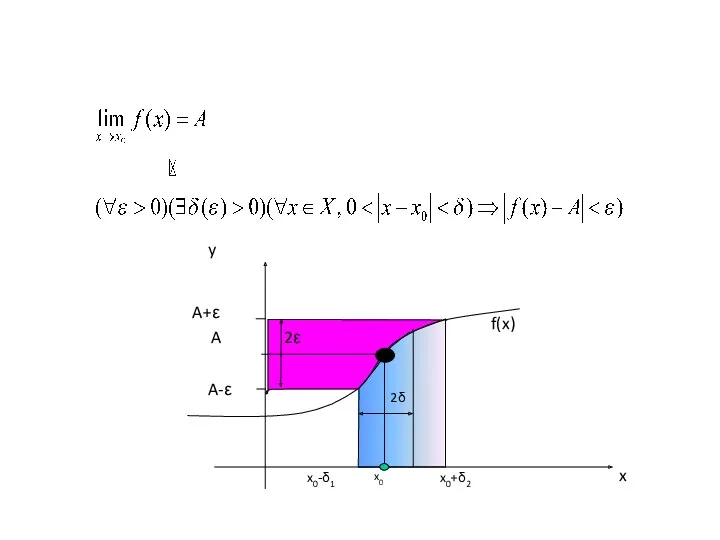
- 17. 2. Предел функции Пусть функция f(x) определена в некоторой окрестности точки x0∈ℝ̄ , кроме, может быть,
- 19. Определение предела функции по Гейне (на языке последовательностей) Число A∈ℝ называется пределом функции f(x) при x
- 20. Замечания 1. Свойства пределов функции, правила вычисления пределов функции аналогичны пределам последовательности Самостоятельно их записать, изменяя
- 21. 2) Пусть f: X → Y , ϕ: Y → Z и существуют пределы Тогда сложная
- 22. Функция α(x) называется бесконечно малой (б.м) при x → x0 , если ЛЕММА. Число A∈ℝ является
- 23. Замечательные пределы первый замечательный предел второй замечательный предел СЛЕДСТВИЯ СЛЕДСТВИЯ
- 24. Односторонние пределы правосторонний левосторонний Число A∈ℝ называется пределом функции f(x) при x → x0 слева (в
- 25. ТЕОРЕМА (необходимое и достаточное условие существования предела функции) Функция f(x) имеет предел при x → x0
- 26. 3. Непрерывность функции, точки разрыва Пусть f(x) определена в некоторой окрестности точки x0 Функция f(x) называется
- 27. Замечание В силу теоремы о существовании предела равенство (1) можно записать в виде – определение непрерывности
- 28. Функция f(x) называется непрерывной на интервале (a; b) если она непрерывна в каждой точке этого интервала
- 29. Если функция f(x) определена в некоторой окрестности точки x0 , но не является непрерывной в этой
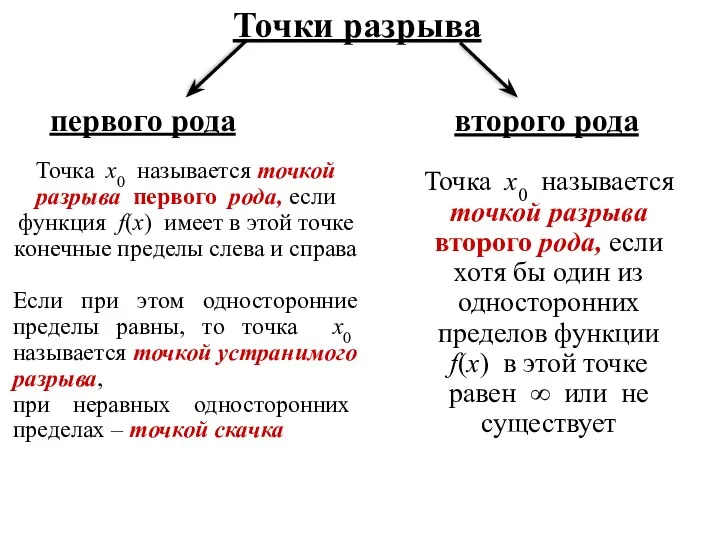
- 30. Точки разрыва первого рода второго рода Точка x0 называется точкой разрыва первого рода, если функция f(x)
- 31. Алгоритм исследования функции на непрерывность Найти точки, подозрительные на разрыв. (точки, в которых функция не определена
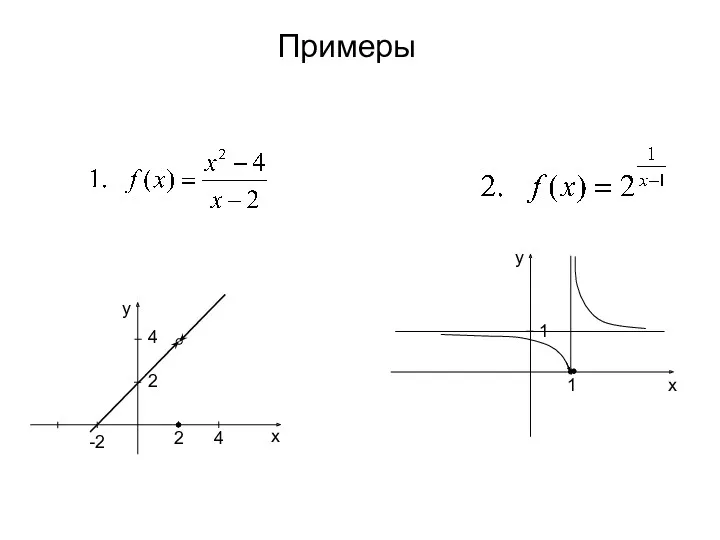
- 32. Примеры
- 34. Скачать презентацию



























 Вычитание удобным способом
Вычитание удобным способом Признаки деления на 3, на 9
Признаки деления на 3, на 9 Физкультминутка(презентация)
Физкультминутка(презентация) Транспортная задача
Транспортная задача Некоторые свойства прямоугольного треугольника. Урок 47
Некоторые свойства прямоугольного треугольника. Урок 47 Равные треугольники. Высота, биссектриса, медиана. 7 класс
Равные треугольники. Высота, биссектриса, медиана. 7 класс Формулы сокращенного умножения
Формулы сокращенного умножения устный счет
устный счет Сумматор
Сумматор Презентация Ох, уж эта математика
Презентация Ох, уж эта математика Свойства функции. 10 класс
Свойства функции. 10 класс Геометрический смысл производной. Подготовка к ЕГЭ
Геометрический смысл производной. Подготовка к ЕГЭ Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Счастливый случай. Игра
Счастливый случай. Игра Инновационный опыт
Инновационный опыт Задачи на нахождение значений параметра
Задачи на нахождение значений параметра Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива.
Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива. Прямоугольная система координат на плоскости. 6 класс
Прямоугольная система координат на плоскости. 6 класс Ряд натуральных чисел
Ряд натуральных чисел Многогранники и их виды
Многогранники и их виды Понятие движения в геометрии
Понятие движения в геометрии Системы двух уравнений с двумя неизвестными. 7 класс
Системы двух уравнений с двумя неизвестными. 7 класс Треугольники. Виды треугольников. Основные свойства треугольников
Треугольники. Виды треугольников. Основные свойства треугольников Decimals
Decimals Взаимно простые числа. Признак делимости на произведение
Взаимно простые числа. Признак делимости на произведение Сложение и вычитание векторов
Сложение и вычитание векторов устный счёт в виде теста 2 класс Табличное умножение
устный счёт в виде теста 2 класс Табличное умножение Перпендикулярные прямые. Решение задач
Перпендикулярные прямые. Решение задач