Содержание
- 2. 1. Предел функции. Теоремы о пределах функции.
- 3. Число зависит от , при уменьшении уменьшается и . Если А – это предел f(x) в
- 4. Пример 1. а) Вычислите предел: б) Вычислите следующий предел:
- 5. Бесконечно большие величины. Ограниченные функции. Бесконечно малые величины и их свойства. - бесконечно большая величина Переменная
- 6. Основные теоремы о бесконечно малых. 1. Алгебраическая сумма любого конечного числа бесконечно малых есть также величина
- 7. Теоремы о пределах. Теорема 1. Предел алгебраической суммы конечного числа слагаемых равен сумме пределов этих слагаемых.
- 8. Теорема 3. Предел частного двух переменных равен частному их пределов, если только предел знаменателя отличен от
- 9. Замечательные пределы
- 10. Теорема 4. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен 1:
- 11. Раскрытие неопределенностей
- 12. Существуют неопределенности следующих видов: 1) 2) 3) 4) 5)
- 13. Неопределенность 1 правило Лопиталя: 1 замечательный предел ( формулу см. ранее). Неопределенность 2 правило Лопиталя (также
- 14. Пример 2. а) Вычислите предел: б) Вычислите следующий предел:
- 15. Пример 3. а) Вычислите предел: б) Вычислите следующий предел:
- 16. Неопределенность Метод решения: используется 2-ой замечательный предел (формулу см. ранее).
- 17. 3. Непрерывность функции. Определение 7. Функция y=f(x) называется непрерывной в точке х0, если бесконечно малому приращению
- 18. 4. Классификация точек разрыва. Разрыв в точке х=х0 имеет место, если нарушено хотя бы одно из
- 20. Скачать презентацию

















 Сумма первых n-членов арифметической прогрессии
Сумма первых n-членов арифметической прогрессии Умные задачки
Умные задачки Переход к новому основанию логарифма
Переход к новому основанию логарифма Понятие квадратного корня из неотрицательного числа
Понятие квадратного корня из неотрицательного числа Паралельне проектування та його властивості
Паралельне проектування та його властивості Математика Стрелки часов
Математика Стрелки часов Квадратичная функция и её график
Квадратичная функция и её график Аналитическая геометрия. Линии на плоскости и их уравнения. Прямая линия на плоскости
Аналитическая геометрия. Линии на плоскости и их уравнения. Прямая линия на плоскости Поняття про об’єм тіла. Основні властивості об’ємів. Об’єм прямокутного паралелепіпеда
Поняття про об’єм тіла. Основні властивості об’ємів. Об’єм прямокутного паралелепіпеда Обыкновенные дроби. Урок-мозаика
Обыкновенные дроби. Урок-мозаика Решение логических задач на уроках математики
Решение логических задач на уроках математики Округление десятичных дробей. Урок математики в 5 классе
Округление десятичных дробей. Урок математики в 5 классе Линейная функция и её график. Устная работа
Линейная функция и её график. Устная работа Таблица умножения. Обобщение
Таблица умножения. Обобщение Расстояние между точками координатной прямой
Расстояние между точками координатной прямой Вычисление первообразных функции
Вычисление первообразных функции Определение декартовых координат. Координаты середины отрезка. Расстояние между точками
Определение декартовых координат. Координаты середины отрезка. Расстояние между точками Математика 3 класс Задачи на кратное сравнение
Математика 3 класс Задачи на кратное сравнение Материалы к урокам математики, УМК Планета знаний, 1 класс
Материалы к урокам математики, УМК Планета знаний, 1 класс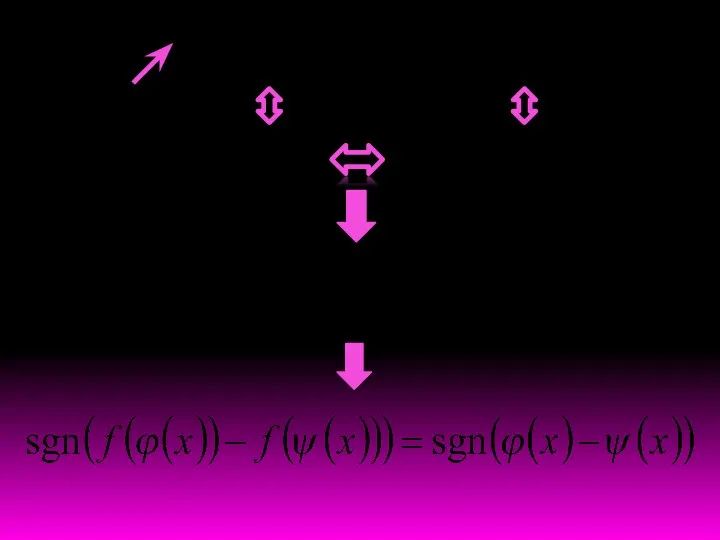 Рационализация неравенства
Рационализация неравенства Конус
Конус Комбинаторное правило умножения. Урок №2
Комбинаторное правило умножения. Урок №2 Виды задач на дроби
Виды задач на дроби Метрология. Калибровка средств измерений. (Лекция 4)
Метрология. Калибровка средств измерений. (Лекция 4) Смежные углы
Смежные углы Последовательность выполнения действий в выражении
Последовательность выполнения действий в выражении Решение задач. Сумма углов треугольника. Внешний угол треугольника
Решение задач. Сумма углов треугольника. Внешний угол треугольника Дробные выражения. Урок математики в 6 классе
Дробные выражения. Урок математики в 6 классе