Содержание
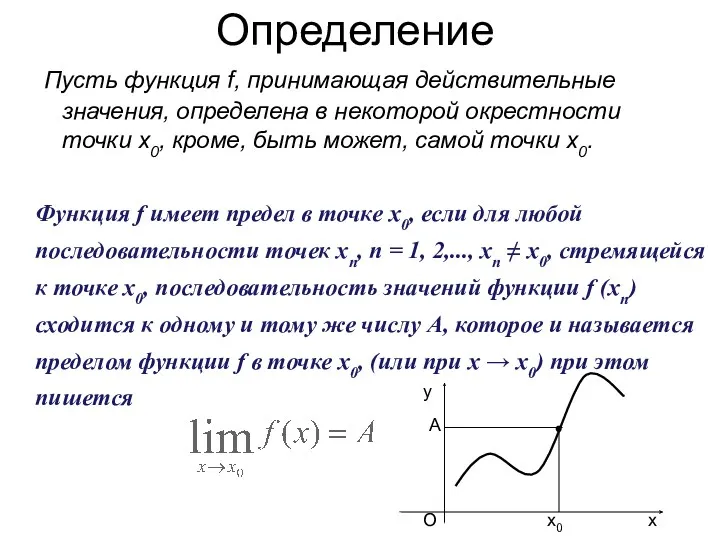
- 2. Определение Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может,
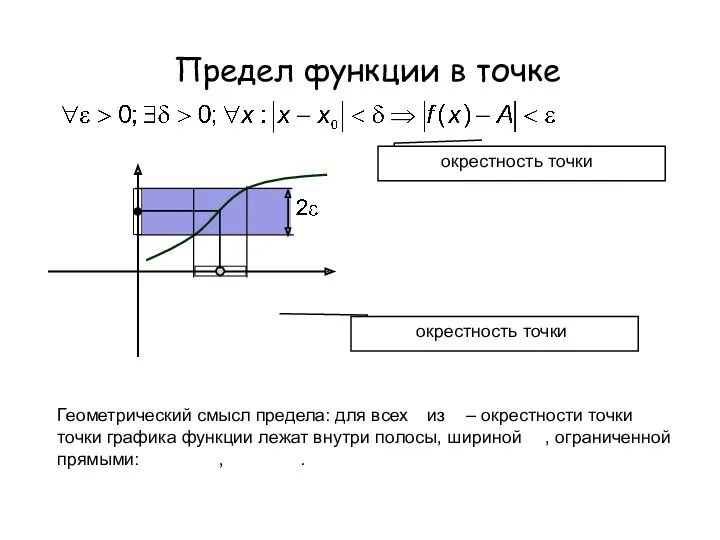
- 3. Предел функции в точке х0 А δ окрестность точки x0 ε окрестность точки А Геометрический смысл
- 4. Определение Число А называется пределом функции f в точке x0, если для любого числа ε >
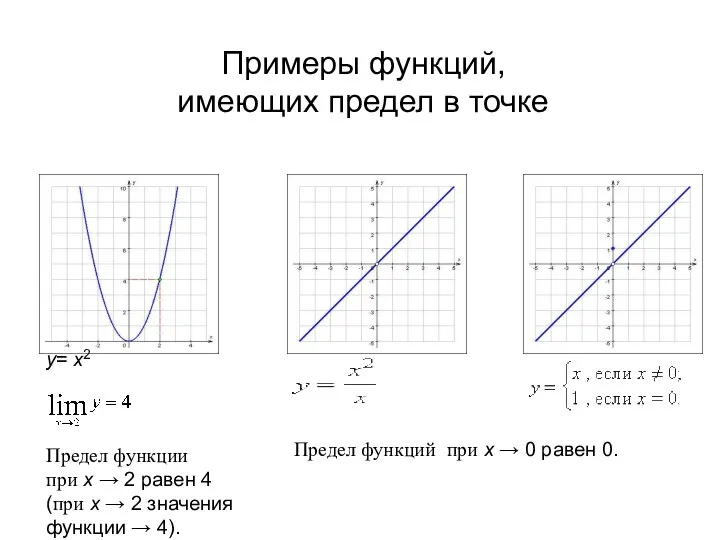
- 5. Примеры функций, имеющих предел в точке у= x2 Предел функции при x → 2 равен 4
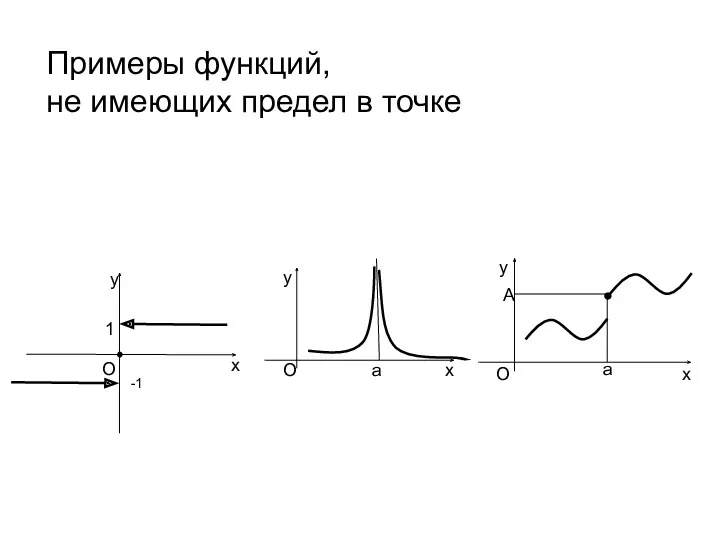
- 6. Примеры функций, не имеющих предел в точке
- 7. Основные теоремы о пределах Рассмотрим теоремы, которые облегчают нахождение пределов функций. Предел суммы (разности) двух функций
- 8. Основные теоремы о пределах Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя
- 9. Основные теоремы о пределах Если между соответствующими значениями трех функций при этом: тогда: выполняются неравенства: Если
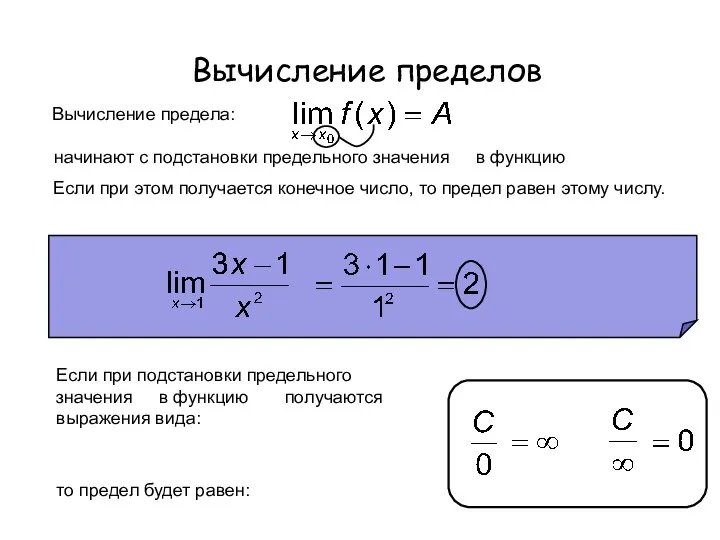
- 10. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
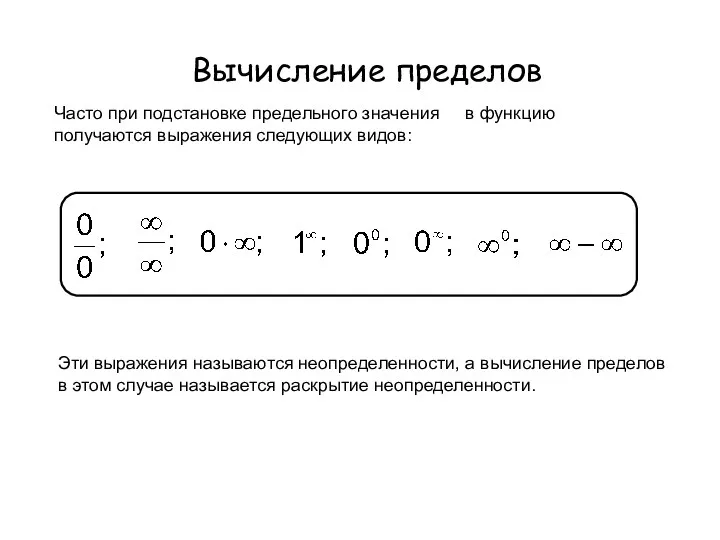
- 11. Вычисление пределов Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов: Эти
- 12. Вычисление предела функции в точке Найдем Предел числителя Предел знаменателя . Используя теорему о пределе частного,
- 13. Найдем Предел числителя Предел знаменателя равен нулю, поэтому теорему о пределе частного применять нельзя. Величина 1/(x-3)
- 14. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель
- 15. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить
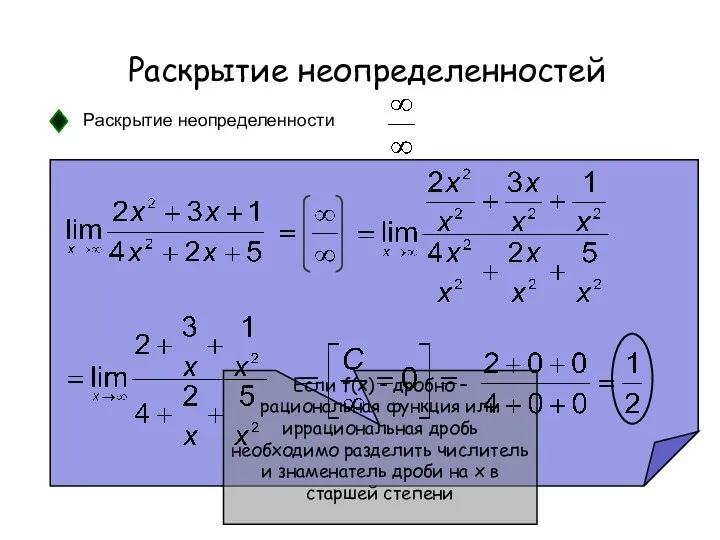
- 16. Раскрытие неопределенности Для того, чтобы раскрыть неопределенность ∞/∞ необходимо разделить числитель и знаменатель на х в
- 17. Разделим числитель и знаменатель на х4
- 18. Разделим числитель и знаменатель на х2 подразумевается не деление на ноль (делить на ноль нельзя), а
- 19. Раскрытие неопределенностей Раскрытие неопределенности Умножим и разделим функцию на сопряженное выражение.
- 21. Решить:
- 23. Скачать презентацию













 Состязание юных математиков
Состязание юных математиков Три подхода к построению множества целых чисел. (Часть 6)
Три подхода к построению множества целых чисел. (Часть 6) Случаи сложения и вычитания основанные на знаниях нумерации
Случаи сложения и вычитания основанные на знаниях нумерации Деление на десятичную дробь
Деление на десятичную дробь Математикадан ачык дәрес 4 класс
Математикадан ачык дәрес 4 класс Случаи вычитания 11-
Случаи вычитания 11- Логарифмы и их применение
Логарифмы и их применение Метрология и метрологическое обеспечение
Метрология и метрологическое обеспечение Бесінші нөмір
Бесінші нөмір Окружность
Окружность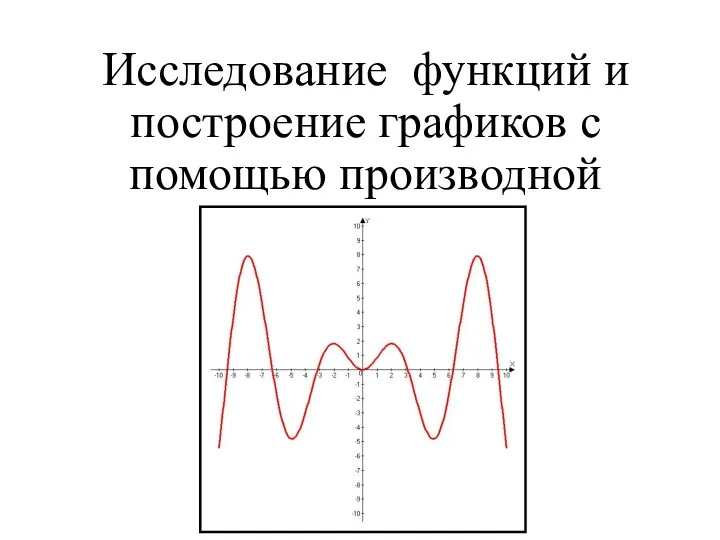 Исследование функций и построение графиков с помощью производной
Исследование функций и построение графиков с помощью производной Сложение вида: +5
Сложение вида: +5 Площади многоугольников
Площади многоугольников Ықтималдылықтар теориясының элементтері дегеніміз не
Ықтималдылықтар теориясының элементтері дегеніміз не Неравенства и системы неравенств с двумя переменными
Неравенства и системы неравенств с двумя переменными Геометрическое место точек. Окружность и круг
Геометрическое место точек. Окружность и круг Әй, осы математика
Әй, осы математика Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Выборочный метод
Выборочный метод Параллельность двух прямых в пространстве
Параллельность двух прямых в пространстве Измерение отрезков. Блиц-опрос. Геометрия 7 класс
Измерение отрезков. Блиц-опрос. Геометрия 7 класс Величина угла. Измерение углов
Величина угла. Измерение углов Множественная регрессия и корреляция
Множественная регрессия и корреляция Способы решения систем линейных уравнений
Способы решения систем линейных уравнений Круглые числа
Круглые числа Учимся считать до 10
Учимся считать до 10 Пропорции
Пропорции Решение задач по готовым чертежам
Решение задач по готовым чертежам