Содержание
- 2. Содержание: Приращение функции Понятие о производной Определение производной Правила вычисления производной Производная сложной функции Производные тригонометрических
- 3. Приращение функции. Δf=f(x0+ Δ x)-f(x0) конспект
- 4. Определение. Производной функции ƒ в точке х0 называется число, к которому стремится разностное отношение, при Δ
- 5. Понятие о производной. (x2)΄= Δ у/ Δx=(x0+ Δx)2-x02/ Δx=x20+2x Δx+ +Δx2-x02/ Δx=2x0 Δx+ Δx2/ Δx=2x0+Δx→2x0 ↓
- 6. Определение производной. f΄(x0)=lim /Δx →0 f(x0+ Δx)-f(x0)/Δx f (x)-дифференцируема с΄=0; x΄=1; (c x)΄=c (x)΄= c Далее.
- 7. Правило вычисления производных. (u ± v ) ΄ = u ΄± v ΄ (u · v
- 8. Производная сложной функции. h ( x ) = g ( f ( x ) ) h
- 9. Производные тригонометрических функций. (sin x) ΄ =cos x (cos x) ΄ = - sin x (tg
- 10. Дифференцирование. Функцию, имеющую производную в точке хо называют дифференцируемой в этой точке. Пусть D1-множество точек, в
- 11. Приращение функции. При сравнении значения функции ƒ в некоторой фиксированной точке х0 значениями этой функции в
- 12. Приращение функции. Эта разность называется приращением Функции ƒ в точке х0 соответствующим приращению Δ х, и
- 13. Производная сложной функции Если функция f имеет производную в точке х0,а функция g имеет производную в
- 14. Приращение функции. Пример 1.Найдем приращения Δ х и Δ f в точке х0 ,если f(х)= Х2
- 15. Производная сложной функции. Пример 1.Найдем производную функции h (x)=(2x+3)100 Функцию h можно представить в виде сложной
- 16. Правила вычисления производных. Правило 1.Если функции U и v дифференцируемое в точке х0 ,то их сумма
- 17. Правила вычисления производных. Пример 1. Найдем производные функций: А) f (x)=x2-1/x (1/x) ΄= - x΄/x2= -1/x2,
- 18. Производные тригонометрических функций. Формула производной синуса. Докажем, что функция синуса имеет производную в любой точке и
- 19. Производные тригонометрических функций. Для вывода формулы достаточно показать ,что а) sinΔx/2/Δx/2→ 1при Δx→ 0; б) cos(x0+Δx/2)
- 20. Формула приближенного вычисления. У=f(x0)+f΄(x0)(x-x0) У ≈f(x0)+f '(x0) Δx
- 21. Производная в физике и технике. Vср (Δt)=Δx/Δt→v(t0) Δx/Δt→x'(t0) V (t)= x´(t) a=v' (t)
- 22. Метод интервалов. 1f Δf →0 при Δ х →0 f (x) →(a) при х →а f
- 23. Метод интервалов. У=k x + b A(x0;f(x0)) У=f '(x) • x + b f(x0)=f´(x0) • x0
- 24. Касательная к графику функции. k=f ´(x0)=tgα f ´(x1)>0; f ´(x2)=0; f ´(x3) f ´(x1)=1; f ´(x2)=0;
- 26. Скачать презентацию























 Степенные функции, свойства, графики
Степенные функции, свойства, графики Решение уравнений, приводимых к квадратным методом введения новой переменной
Решение уравнений, приводимых к квадратным методом введения новой переменной Случайные события и их вероятность
Случайные события и их вероятность Степени и корни. Иррациональные уравнения
Степени и корни. Иррациональные уравнения Повторение испытаний
Повторение испытаний Игра по математике Считай, смекай, отгадывай
Игра по математике Считай, смекай, отгадывай Геометрия моими глазами. Евклидова и неевклидова геометрия
Геометрия моими глазами. Евклидова и неевклидова геометрия Кут та його величина. Види кутів. 5 клас
Кут та його величина. Види кутів. 5 клас Приёмы устных вычислений вида 450+30, 620-200
Приёмы устных вычислений вида 450+30, 620-200 Действия с дробями. Задачи на движения
Действия с дробями. Задачи на движения Игры (геометрия). Статические игры
Игры (геометрия). Статические игры Арифметическая прогрессия
Арифметическая прогрессия Занимательные задачи
Занимательные задачи Деление многозначных чисел на трёхзначное число
Деление многозначных чисел на трёхзначное число Действия с обыкновенными дробями. Считаем устно
Действия с обыкновенными дробями. Считаем устно Натуральные числа и нуль. Измерение величин. Математика. 5 класс
Натуральные числа и нуль. Измерение величин. Математика. 5 класс Производная. Понятие о производной
Производная. Понятие о производной Математик – бизнесмен. Математическая игра для 5 классов
Математик – бизнесмен. Математическая игра для 5 классов Решение задач на движение по реке
Решение задач на движение по реке Методы статистического вывода: проверка гипотез
Методы статистического вывода: проверка гипотез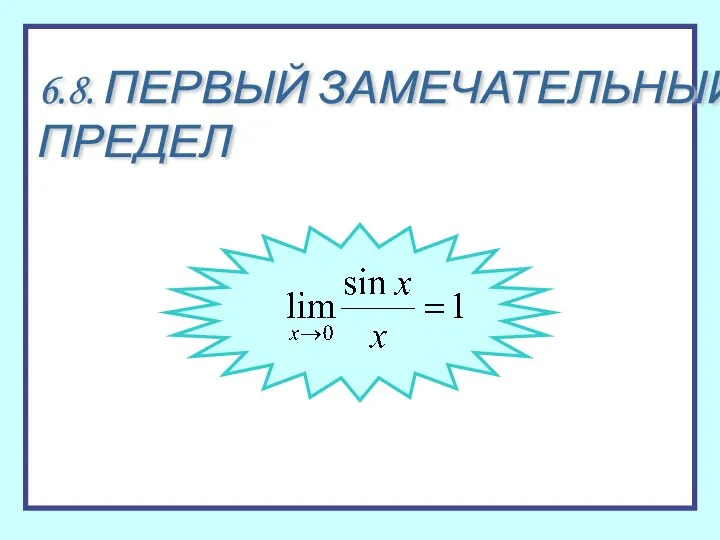 6.8
6.8 Рекордсмены царства животных. Математика. 5 класс
Рекордсмены царства животных. Математика. 5 класс Цена, количество, стоимость. Задачи
Цена, количество, стоимость. Задачи Векторная алгебра
Векторная алгебра Компьютерное моделирование как метод научного познания
Компьютерное моделирование как метод научного познания Мәтінді есептерді шығару
Мәтінді есептерді шығару Решение задач с использованием формулы полной вероятности и формулы Бейеса
Решение задач с использованием формулы полной вероятности и формулы Бейеса Развитие теории вероятностей. Основные элементы комбинаторики
Развитие теории вероятностей. Основные элементы комбинаторики