Содержание
- 2. Расстояние от точки до плоскости
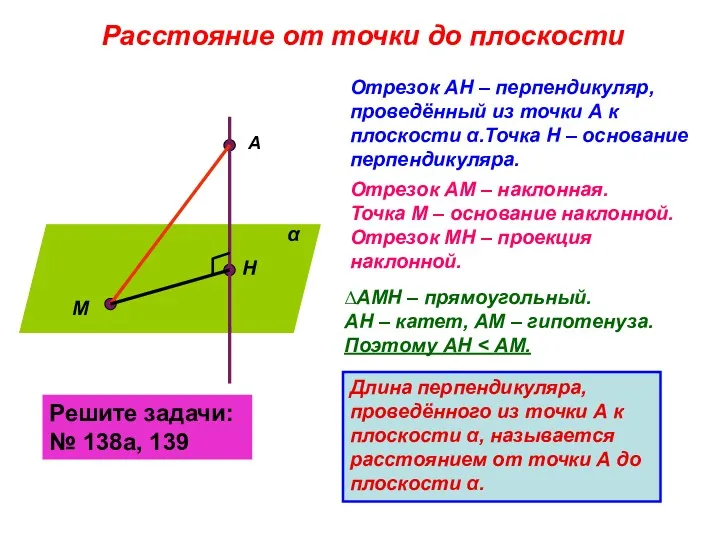
- 3. Расстояние от точки до плоскости α А Н М Отрезок АН – перпендикуляр, проведённый из точки
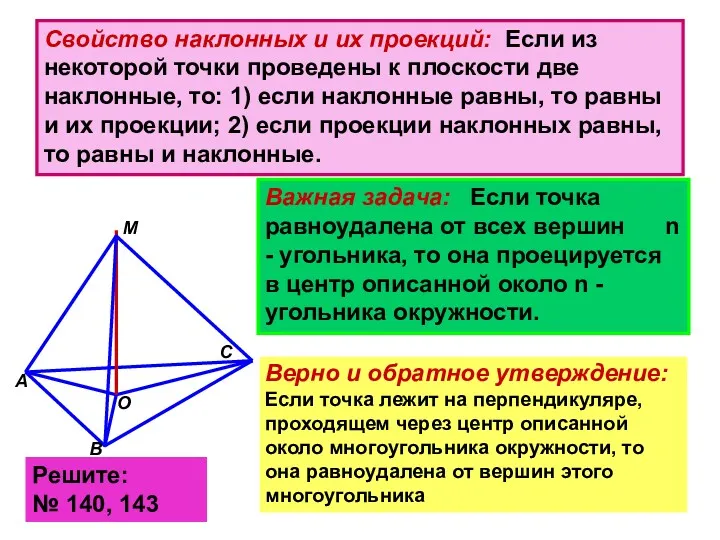
- 4. Свойство наклонных и их проекций: Если из некоторой точки проведены к плоскости две наклонные, то: 1)
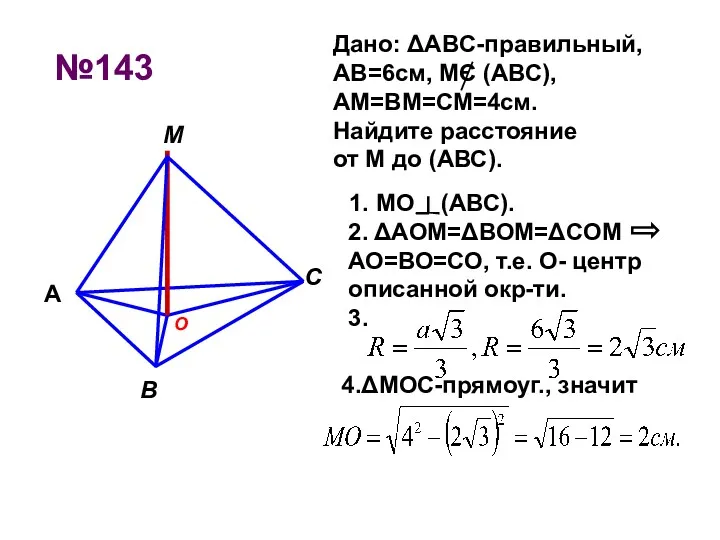
- 5. №143 1. МО (АВС). 2. ΔAOM=ΔBOM=ΔCOM АО=ВО=СО, т.е. О- центр описанной окр-ти. 3. 4.ΔMOC-прямоуг., значит В
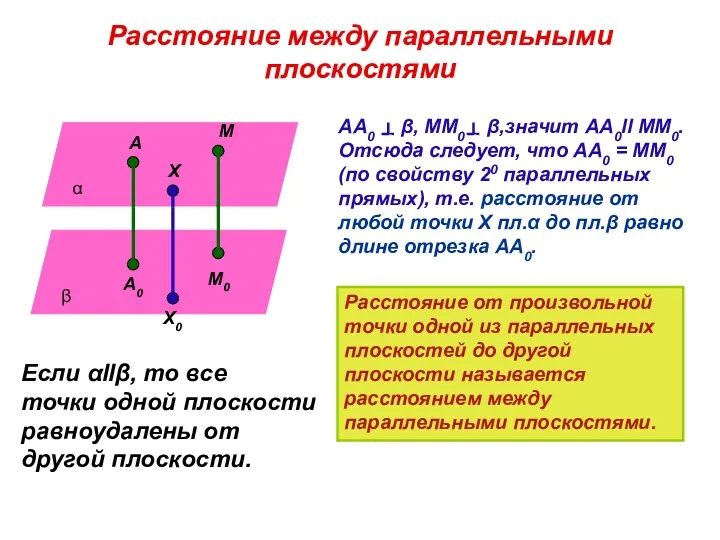
- 6. Расстояние между параллельными плоскостями А М А0 М0 Х Х0 α β АА0 β, ММ0 β,значит
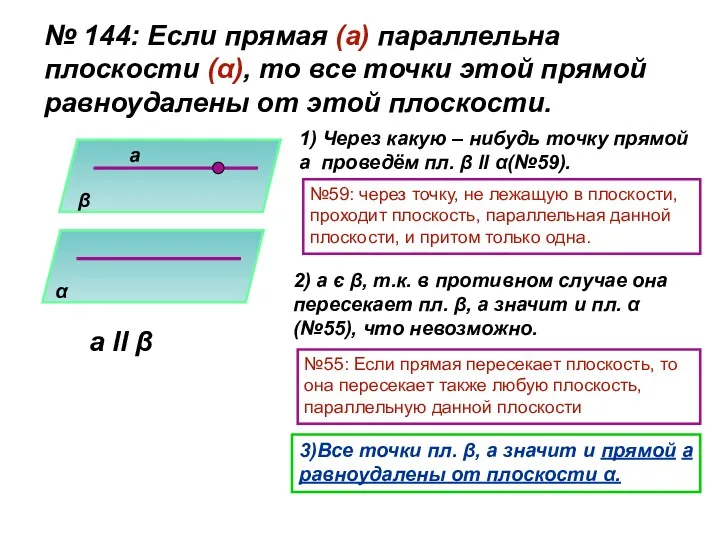
- 7. № 144: Если прямая (а) параллельна плоскости (α), то все точки этой прямой равноудалены от этой
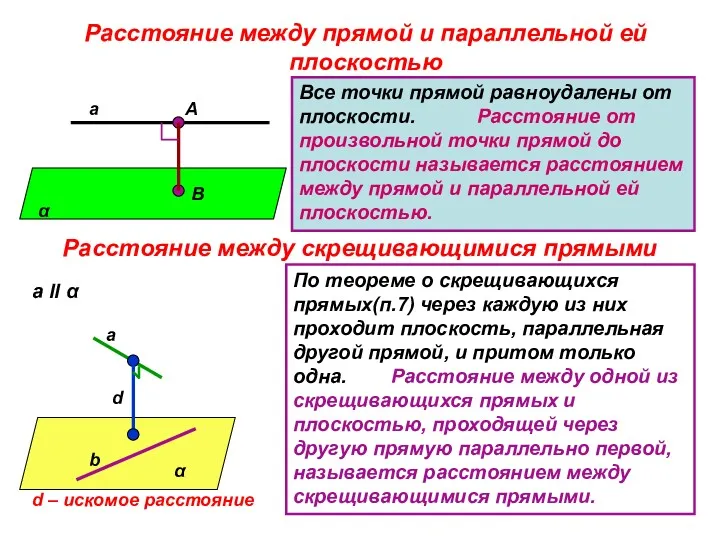
- 8. Расстояние между прямой и параллельной ей плоскостью а α А В Все точки прямой равноудалены от
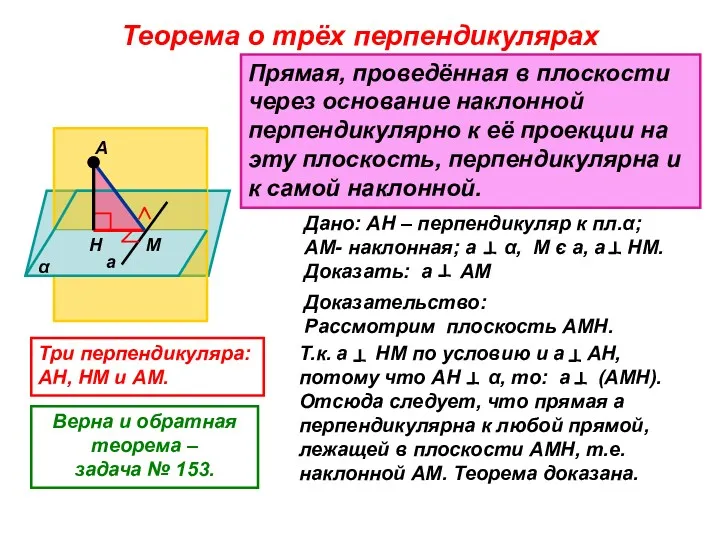
- 9. Теорема о трёх перпендикулярах
- 10. Теорема о трёх перпендикулярах α А Н М а Прямая, проведённая в плоскости через основание наклонной
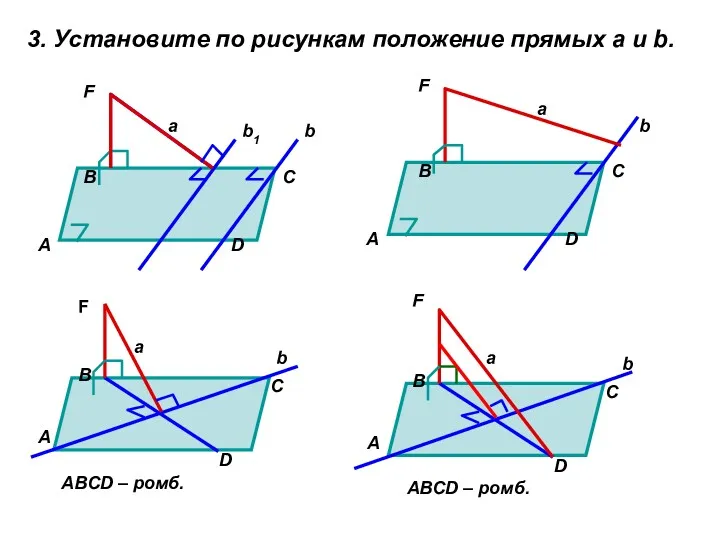
- 11. 3. Установите по рисункам положение прямых а и b. А В С D b а F
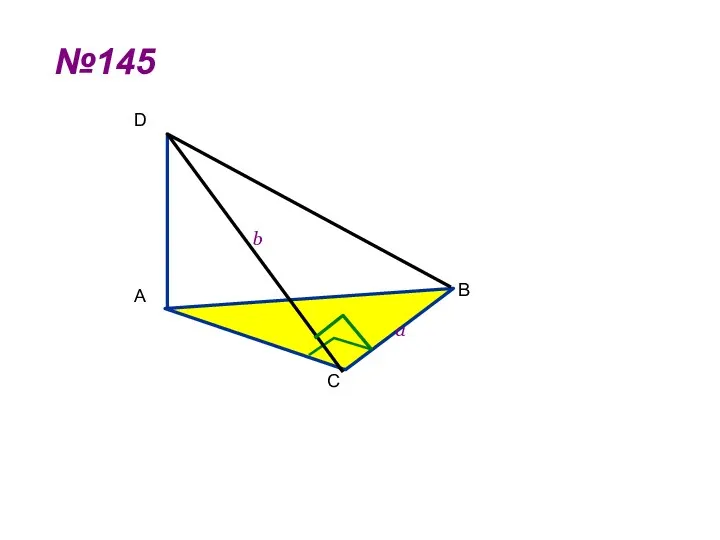
- 12. №145 C A D B a b
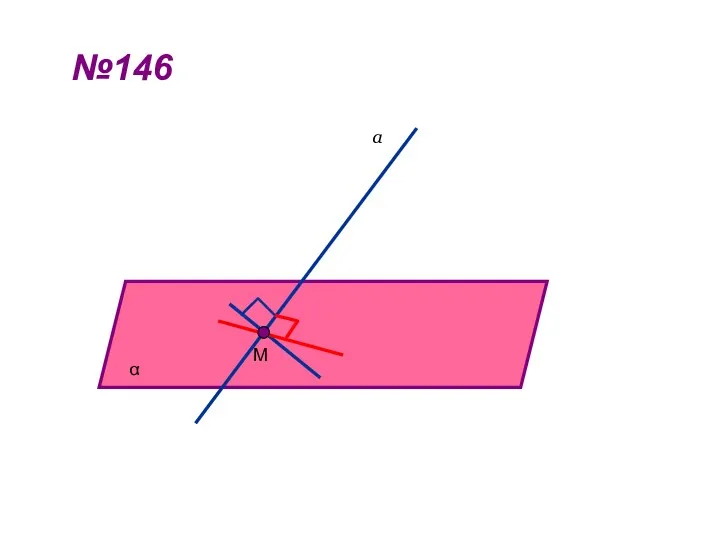
- 13. №146 α а М
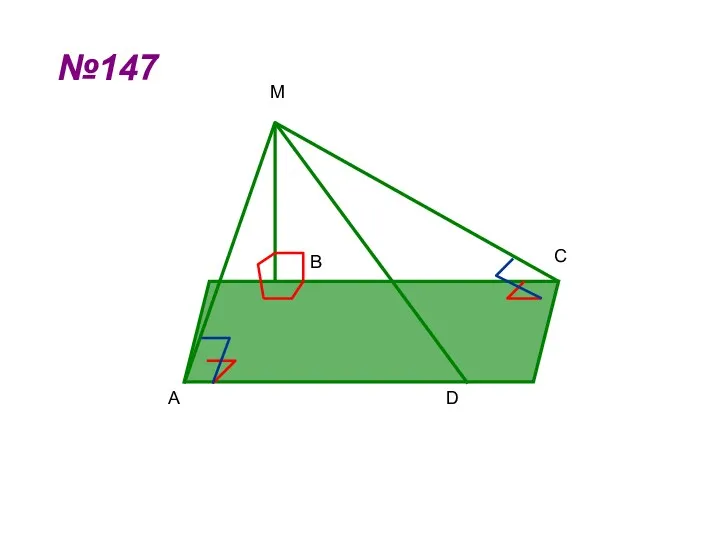
- 14. №147 А В С D M
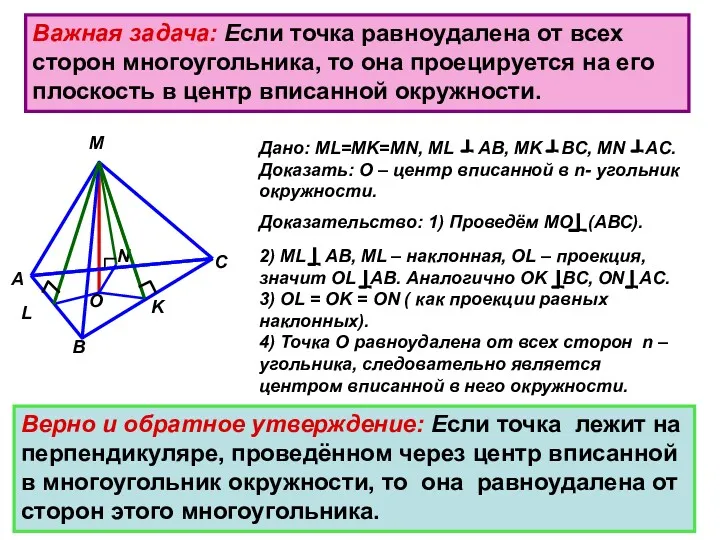
- 15. Важная задача: Если точка равноудалена от всех сторон многоугольника, то она проецируется на его плоскость в
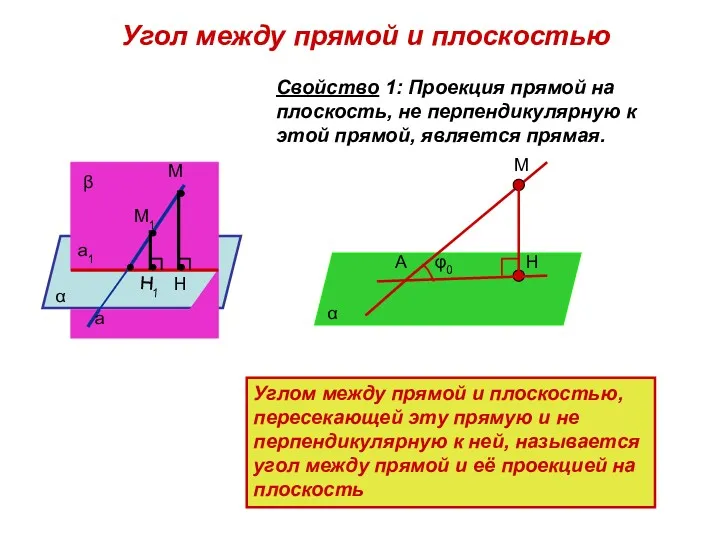
- 16. Угол между прямой и плоскостью
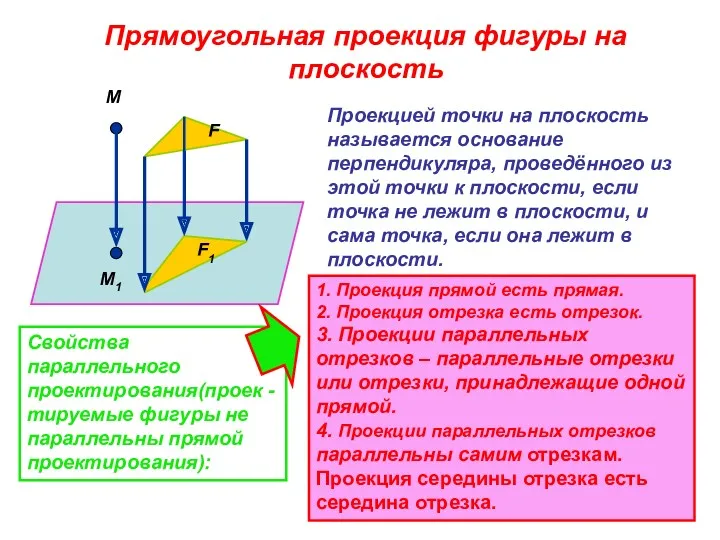
- 17. Прямоугольная проекция фигуры на плоскость М М1 F F1 Проекцией точки на плоскость называется основание перпендикуляра,
- 18. Свойство 1: Проекция прямой на плоскость, не перпендикулярную к этой прямой, является прямая. Угол между прямой
- 20. Скачать презентацию



 Вероятность и статистика. Операции над множествами: объединение, пересечение, дополнение
Вероятность и статистика. Операции над множествами: объединение, пересечение, дополнение Координаты на плоскости. 6 класс
Координаты на плоскости. 6 класс Квадрат суммы и квадрат разности для матриц размером 2х2
Квадрат суммы и квадрат разности для матриц размером 2х2 Вычитание вида 11 - …, 12 - …
Вычитание вида 11 - …, 12 - … Презентация по математике , 1 класс, тема Числа 0-9. Закрепление.
Презентация по математике , 1 класс, тема Числа 0-9. Закрепление. Часы, минуты, сутки
Часы, минуты, сутки Трапеция. 6 класс
Трапеция. 6 класс Властивості коренів. Розв′язування задач
Властивості коренів. Розв′язування задач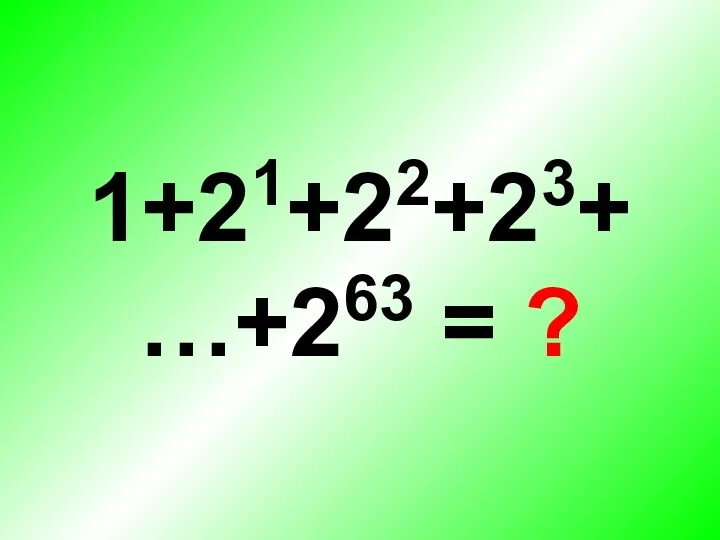 Степень числа. Квадрат и куб числа
Степень числа. Квадрат и куб числа Математика- Устный счет, логические разминки 1 класс
Математика- Устный счет, логические разминки 1 класс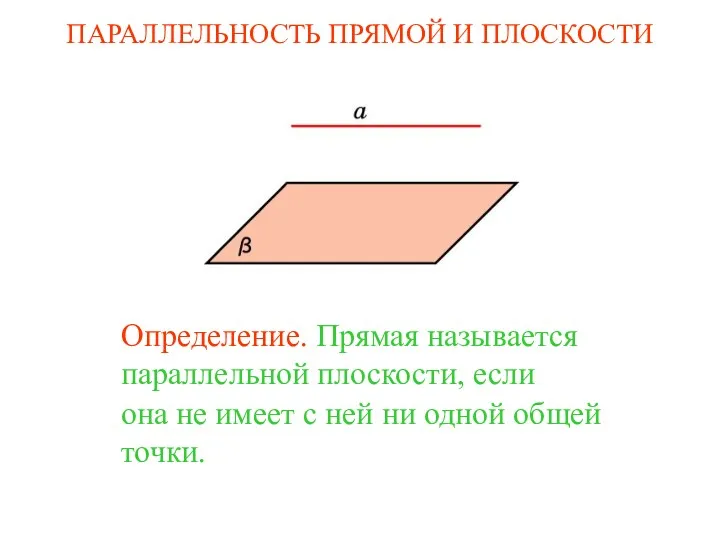 Параллельность прямой и плоскости
Параллельность прямой и плоскости Длина окружности и площадь круга
Длина окружности и площадь круга Формулы сокращенного умножения. Квадрат выражения
Формулы сокращенного умножения. Квадрат выражения презентация к уроку Математика 4 класс Поупражняемся в действиях над величинами ПНШ
презентация к уроку Математика 4 класс Поупражняемся в действиях над величинами ПНШ Действия с отрицательными и положительными числами на уроках математики и географии
Действия с отрицательными и положительными числами на уроках математики и географии Свойства действий с рациональными числами
Свойства действий с рациональными числами Презентация к уроку математики во 2 классе по теме Периметр
Презентация к уроку математики во 2 классе по теме Периметр Презентация к уроку математики на тему Сложение и вычитание трехзначных чисел
Презентация к уроку математики на тему Сложение и вычитание трехзначных чисел Задачи в координатах II
Задачи в координатах II Метрологические характеристики средств измерения
Метрологические характеристики средств измерения Виды многогранников. Тела Платона
Виды многогранников. Тела Платона Четырёхугольники
Четырёхугольники Урок - презентация Единицы времени
Урок - презентация Единицы времени Элементы теории множеств. Понятие множества
Элементы теории множеств. Понятие множества Математика и космос. Задачи
Математика и космос. Задачи Графическое решение систем уравнений с двумя переменными
Графическое решение систем уравнений с двумя переменными Мүмкінді ауысу әдісі. Қарқынды ауысу әдісі
Мүмкінді ауысу әдісі. Қарқынды ауысу әдісі Урок математики Во 2 классе Тема: Урок повторения изученного с элементами материалов окружающего мира
Урок математики Во 2 классе Тема: Урок повторения изученного с элементами материалов окружающего мира