Содержание
- 3. Кормен Т., Лейзерсон Ч., Ривест Р. «Алгоритмы. Построение и анализ» (главы 1, 2, 4) Левитин А.
- 4. Анализ вычислительной сложности алгоритмов
- 5. Алгоритм Евклида (III в. до н.э)
- 6. Псевдокод
- 7. Псевдокод 1. Отступ от левого поля указывает на уровень вложенности
- 8. Введение Основная задача теории – анализ алгоритмов с целями: определения необходимых объемов ресурсов для решения конкретной
- 9. Ресурсы, расходуемые алгоритмом (вычислительные ресурсы) Вычислительные ресурсы – возможности, обеспечиваемые компонентами вычислительной системы, расходуемые (занимаемые) в
- 10. Абстрактная модель вычислений Основные положения Алгоритм рассматривается как набор операций и управляющих структур. Каждому виду операций
- 11. 1. Алгоритм рассматривается как набор операций и управляющих структур Базовые виды управляющих структур Составной оператор (begin
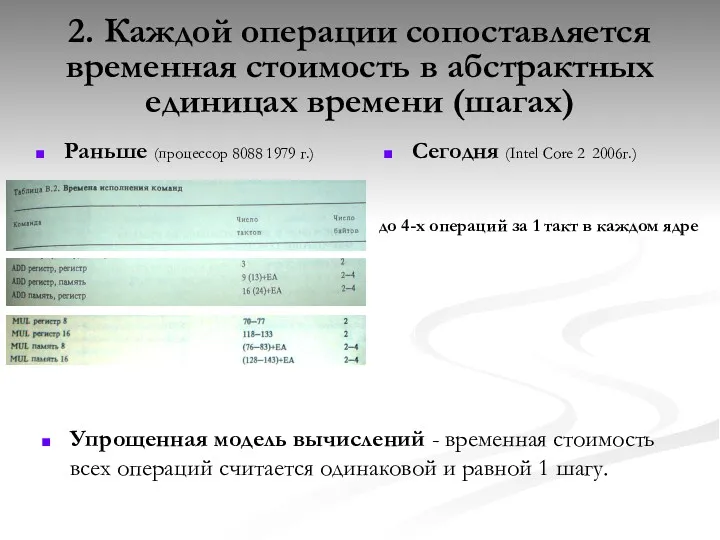
- 12. 2. Каждой операции сопоставляется временная стоимость в абстрактных единицах времени (шагах) Упрощенная модель вычислений - временная
- 13. 3. Время работы алгоритма в целом равно сумме стоимостей составляющих его операций с учетом вложенности управляющих
- 14. Оценка сложности
- 15. Оценка сложности
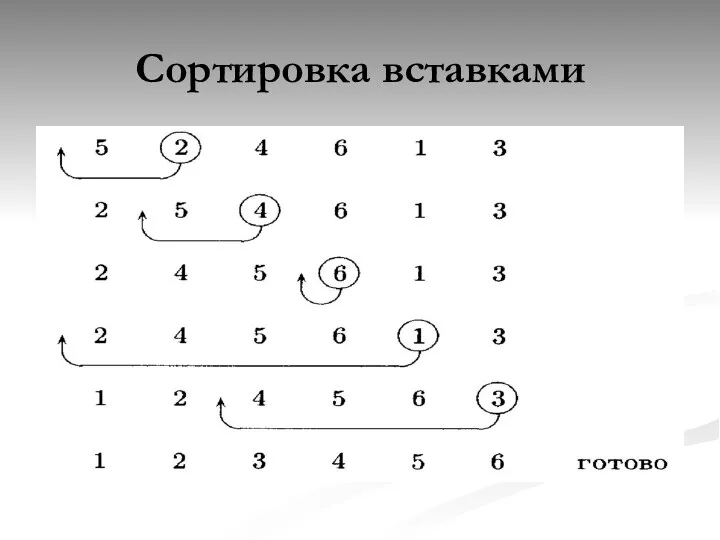
- 16. Сортировка вставками
- 17. Сортировка вставками
- 18. Сортировка вставками
- 19. Худший случай
- 20. Пример анализа вычислительной сложности алгоритма //Алгоритм простого последовательного поиска целого числа x в массиве A function
- 21. Пример анализа вычислительной сложности алгоритма (в упрощенной модели вычислений) //Алгоритм простого последовательного поиска целого числа x
- 22. Зависимость от входных данных Временная сложность поиска числа в массиве зависит от содержимого массива А, от
- 23. Асимптотический анализ вычислительной сложности алгоритмов Асимптотический анализ – анализ поведения функции временной сложности алгоритма Т(n) при
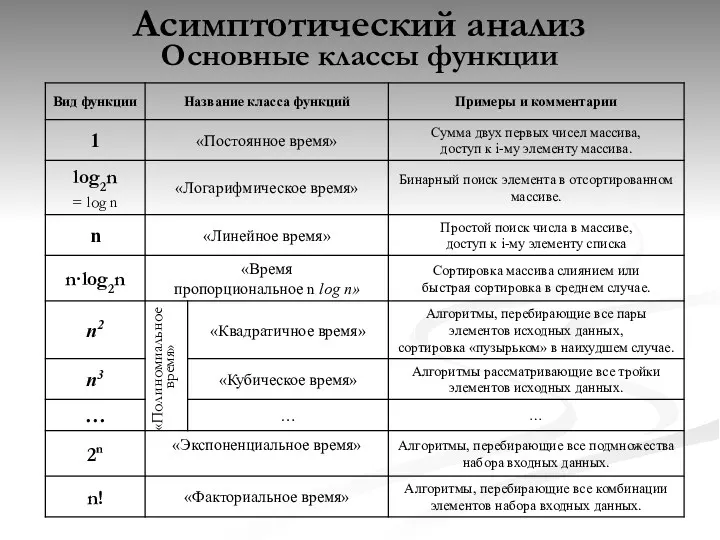
- 24. Асимптотический анализ Основные классы функции «Полиномиальное время»
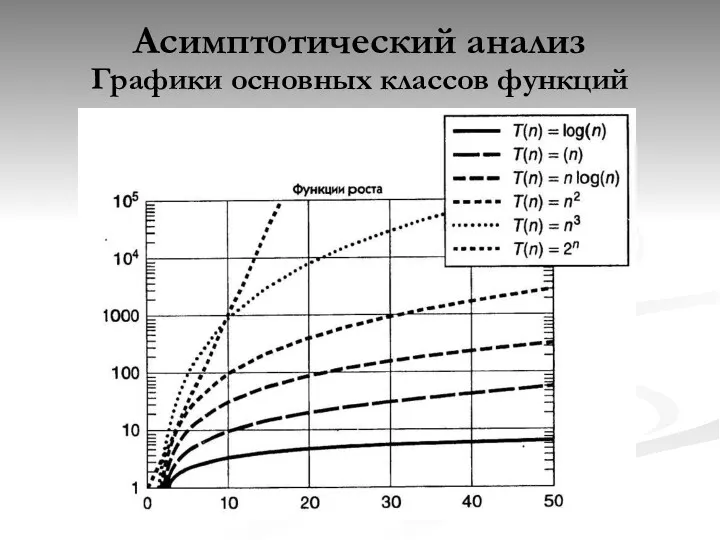
- 25. Асимптотический анализ Графики основных классов функций
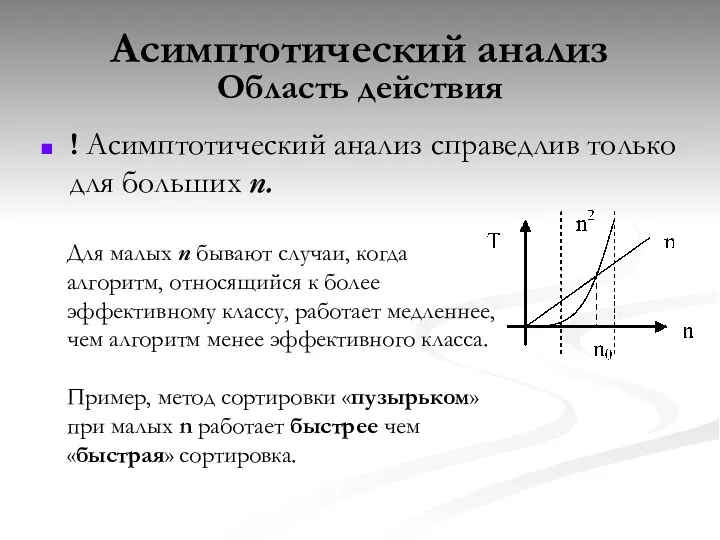
- 26. Асимптотический анализ Область действия ! Асимптотический анализ справедлив только для больших n. Для малых n бывают
- 27. Асимптотический анализ
- 32. Аналогии
- 33. Примеры
- 35. Основные формулы суммирования
- 38. Пример
- 39. Метод итераций
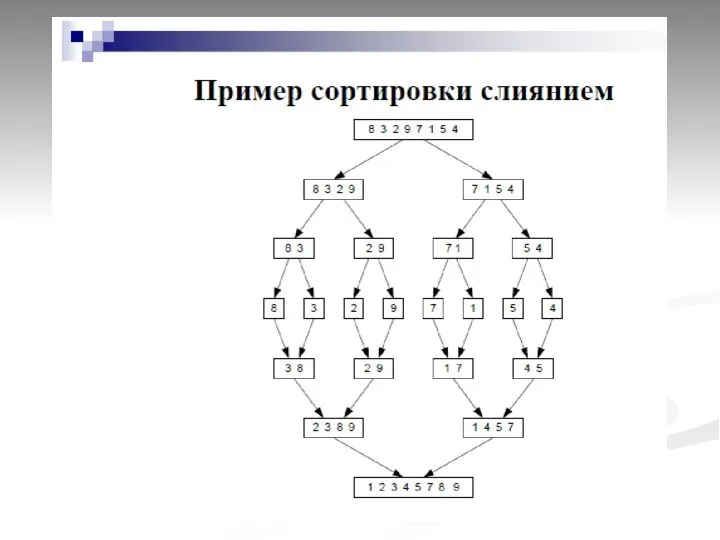
- 42. Сортировка слиянием
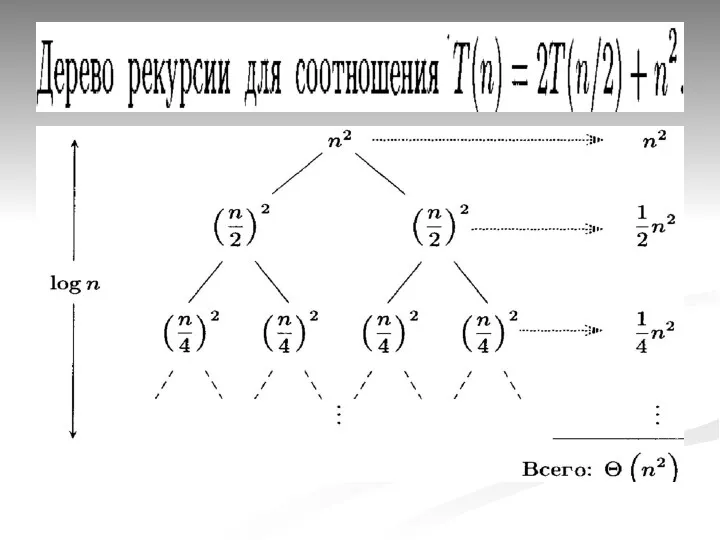
- 43. Анализ
- 46. Скачать презентацию




































 Основные понятия стереометрии
Основные понятия стереометрии Сумма и разность синусов и косинусов
Сумма и разность синусов и косинусов Минимизация переключательных функций по картам Карно
Минимизация переключательных функций по картам Карно Угол. Виды углов. Прямой угол (2 класс)
Угол. Виды углов. Прямой угол (2 класс) Периметр квадрата и прямоугольника. Презентация.
Периметр квадрата и прямоугольника. Презентация. Формулы тригонометрии
Формулы тригонометрии Линейные уравнения с параметрами. 7 класс
Линейные уравнения с параметрами. 7 класс презентация по математике Решение задач в 2 действия
презентация по математике Решение задач в 2 действия Устные задания В2 и В8. ЕГЭ по математике
Устные задания В2 и В8. ЕГЭ по математике Статистические характеристики
Статистические характеристики Основные тригонометрические формулы
Основные тригонометрические формулы Координаталық сәуле. Натурал сандарды координаталық сәуледе салыстыру
Координаталық сәуле. Натурал сандарды координаталық сәуледе салыстыру Тест по математике
Тест по математике Веселый счет
Веселый счет Прямоугольные треугольники. Свойства прямоугольных треугольников
Прямоугольные треугольники. Свойства прямоугольных треугольников Мистика и тайны загадочного числа пи
Мистика и тайны загадочного числа пи Счет в пределах 10, 1 класс Поймай рыбку
Счет в пределах 10, 1 класс Поймай рыбку Matrices: Basic Operations
Matrices: Basic Operations Арифметические действия с натуральными числами. Упражнение 7. 5 класс
Арифметические действия с натуральными числами. Упражнение 7. 5 класс Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Задачи на нахождение неизвестного по двум разностям 4 класс(практичекий материал)
Задачи на нахождение неизвестного по двум разностям 4 класс(практичекий материал) Задачи на взвешивание. Тема №8
Задачи на взвешивание. Тема №8 Система задач по теме Преобразование числовых выражений
Система задач по теме Преобразование числовых выражений Подобные треугольники
Подобные треугольники Мультимедийный путеводитель Математический Петербург: опыт погружения математики в городскую среду
Мультимедийный путеводитель Математический Петербург: опыт погружения математики в городскую среду Числовые выражения, содержащие знаки + и -. Урок-путешествие За сокровищами
Числовые выражения, содержащие знаки + и -. Урок-путешествие За сокровищами Приёмы письменных вычислений
Приёмы письменных вычислений Парабола. Квадратичная функция
Парабола. Квадратичная функция