Содержание
- 2. Цели урока: Развивать математическую речь, мышление и память; Расширить знания по данной теме, рассмотрев различные способы
- 3. «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить
- 4. Во глубь веков Представители различных цивилизаций: Древнего Египта, Древнего Вавилона, Древней Греции, Древней Индии, Древнего Китая,
- 5. Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными
- 6. Диофантовы уравнения Греческий математик Диофант составлял и решал квадратные уравнения. В «Арифметике» Диофанта нет систематического изложения
- 8. В Древней индии Задачи на составление квадратных уравнений встречаются уже в астрономическом трактате «Ариа-бхатиам», составленном в
- 9. Вот одна из задач знаменитого индийского математика XII в. Бхаскары: Обезьянок резвых стая Всласть поевши, развлекалась.
- 10. В Древней Азии Первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX
- 11. Квадратные уравнения в Европе XIII-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду
- 12. Квадратное уравнение Квадратным уравнением называется уравнение вида ax2+bx+c=0, где a, b, с ∈ R (a ≠
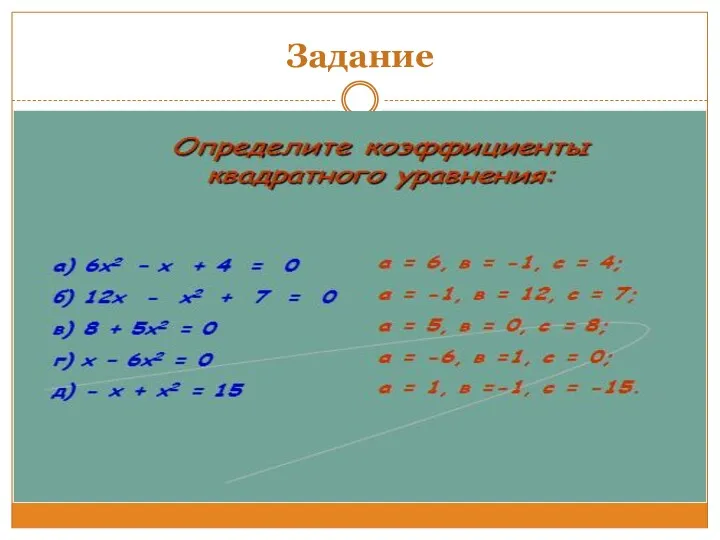
- 13. Задание
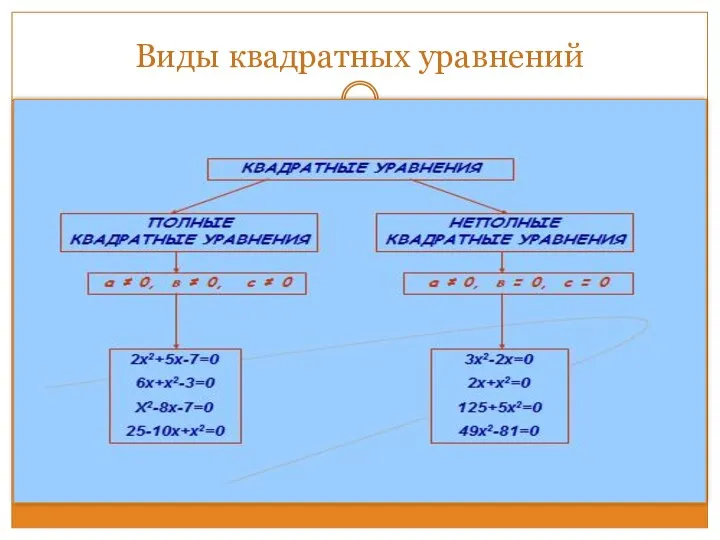
- 14. Виды квадратных уравнений
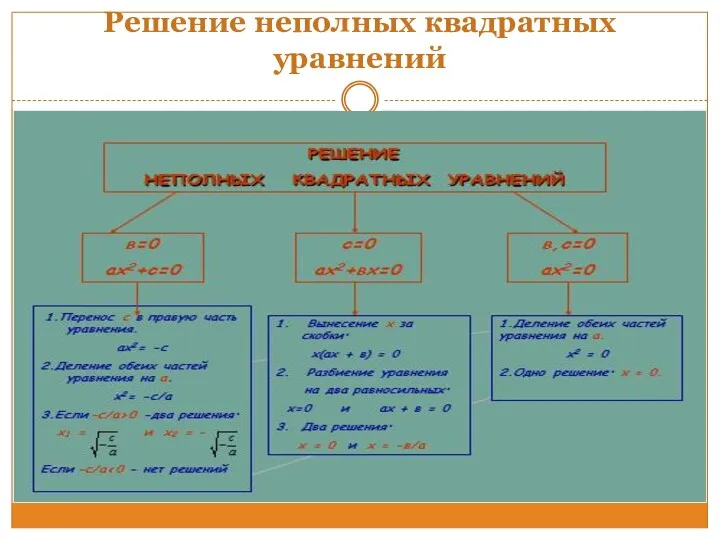
- 15. Решение неполных квадратных уравнений
- 16. Примеры решения неполных квадратных уравнений 6x2 =0, 2x2 - 9x =0 х =0. х(2х – 9)
- 17. Примеры решения неполных квадратных уравнений -2x2+32=0, -2x2 = - 32
- 18. Решение квадратных уравнений по формуле ax2+bx+c=0 Выписать: а =…, в =…, с =… Найдите дискриминант по
- 19. РЕШИТЕ УСТНО: ). x²=0, ). 4x²=0, ). 3x²+12=0, ). 7x²-3x=0, ). -x²+7=0. ОТВЕТЫ: 1) нет решений;
- 20. Пример решения квадратного уравнения по формуле 2x2 – 5x + 2 = 0, а = 2,
- 21. Решите уравнения 3х2 + х – 4 = 0; 10х2 – 11х + 3 = 0;
- 22. О теореме Виета Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета,
- 23. О теореме Виета Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета,
- 24. x1 и х2 – корни уравнения Решение уравнений с помощью теоремы Виета Х2 + 3Х –
- 25. РЕШИТЕ УРАВНЕНИЯ х2 – 2х – 15 = 0; х2 + 2х – 8 = 0;
- 26. Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета
- 27. Второй коэффициент - четный
- 28. Решим уравнение: х2 + 6х - 7 = 0. х2 + 6х -7 = 0. (х
- 29. РЕШИ УРАВНЕНИЯ с помощью формулы : 1 вариант: а) -7х + 5х2 + 1 =0 б)
- 31. Скачать презентацию

























 Дистанционный урок по математике 10 марта 2014 года
Дистанционный урок по математике 10 марта 2014 года Умножение и деление на 3. Треть числа.
Умножение и деление на 3. Треть числа. Подготовка к ЕГЭ по математике. Решение заданий В3
Подготовка к ЕГЭ по математике. Решение заданий В3 урок математики в 3 классе Умножение многозначного на однозначное число по программе Начальная школа 21 век
урок математики в 3 классе Умножение многозначного на однозначное число по программе Начальная школа 21 век Работа с матрицами и решение систем линейных алгебраических уравнений
Работа с матрицами и решение систем линейных алгебраических уравнений Отношения и пропорции
Отношения и пропорции Презентация по математике по теме Логарифм для 10-11 класса
Презентация по математике по теме Логарифм для 10-11 класса Порядок возрастания числа
Порядок возрастания числа Цена, количество, стоимость. Решение задач
Цена, количество, стоимость. Решение задач Дидактическая игра по ФЭМП Помоги Буратино достать ключик (подготовительная группа).
Дидактическая игра по ФЭМП Помоги Буратино достать ключик (подготовительная группа). Делители. Наибольший общий делитель. Наименьшее общее кратное
Делители. Наибольший общий делитель. Наименьшее общее кратное Прямая и кривая линии. (1 класс)
Прямая и кривая линии. (1 класс) Теорема о равенстве односторонних углов. Теорема о свойстве односторонних углов
Теорема о равенстве односторонних углов. Теорема о свойстве односторонних углов Красота и гармония в симметрии
Красота и гармония в симметрии Порядок действий.
Порядок действий. шар и сфера (1)
шар и сфера (1) Задачи на разрезание и складывание фигур. Наглядная геометрия. 5 класс
Задачи на разрезание и складывание фигур. Наглядная геометрия. 5 класс Презентация к уроку математики Решение задач на одновременное движение
Презентация к уроку математики Решение задач на одновременное движение Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Учимся определять время по часам
Учимся определять время по часам Приемы вычислений для случаев вида 26+4, 30-7.
Приемы вычислений для случаев вида 26+4, 30-7. Случаи сложения вида +4
Случаи сложения вида +4 Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems
Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems Prisma. Definiţii, notaţii
Prisma. Definiţii, notaţii Интеграл от функции комплексного переменного. Теорема Коши (доказательство). Многозначные функции
Интеграл от функции комплексного переменного. Теорема Коши (доказательство). Многозначные функции Последовательность комплексных чисел
Последовательность комплексных чисел Диэлектрическая проницаемость сред с временной и пространственной дисперсией. (Лекция 3)
Диэлектрическая проницаемость сред с временной и пространственной дисперсией. (Лекция 3) Статистикалық бақылау
Статистикалық бақылау