Содержание
- 2. РЕШЕНИЕ УРАВНЕНИЙ Решить уравнение – значит найти множество всех корней этого уравнения. При решении практических задач:
- 3. КЛАССЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В зависимости от того, какие функции входят в уравнение f(x)=0, уравнения разделяются на
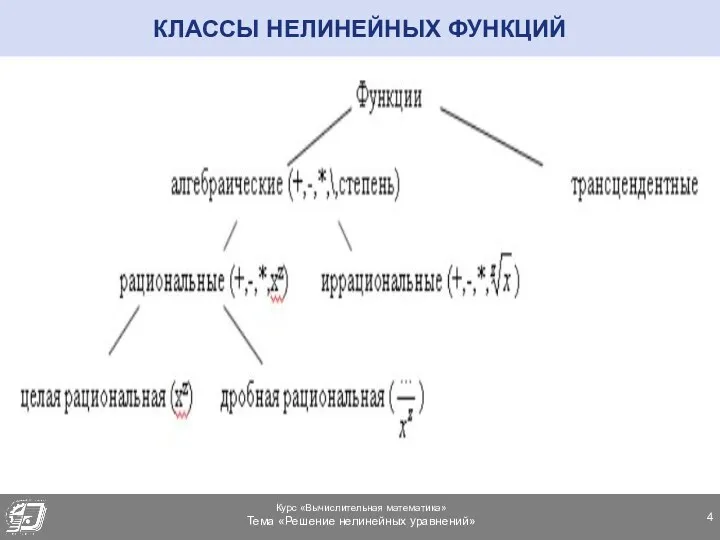
- 4. КЛАССЫ НЕЛИНЕЙНЫХ ФУНКЦИЙ
- 5. АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ Алгебраическая функция – функция, содержащая арифметические операции (+, -, *, \ ) и возведение
- 6. Пример рациональной алгебраической функции Рациональная алгебраическая функция:
- 7. ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ Целая рациональная алгебраическая функция: Иррациональная алгебраическая функция:
- 8. АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ Дробно-рациональная алгебраическая функция:
- 9. ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ Трансцендентные функции – все неалгебраические функции: показательная ax , логарифмическая logax , тригонометрические sinx,
- 10. ЭТАПЫ НАХОЖДЕНИЙ КОРНЯ Процесс нахождения приближенных значений корней уравнения разбивается на 2 этапа: 1) отделение корней,
- 11. ЛОКАЛИЗАЦИЯ КОРНЕЙ Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом
- 12. СПОСОБЫ ОТДЕЛЕНИЯ КОРНЕЙ Отделение корней можно произвести двумя методами: графическим, аналитическим.
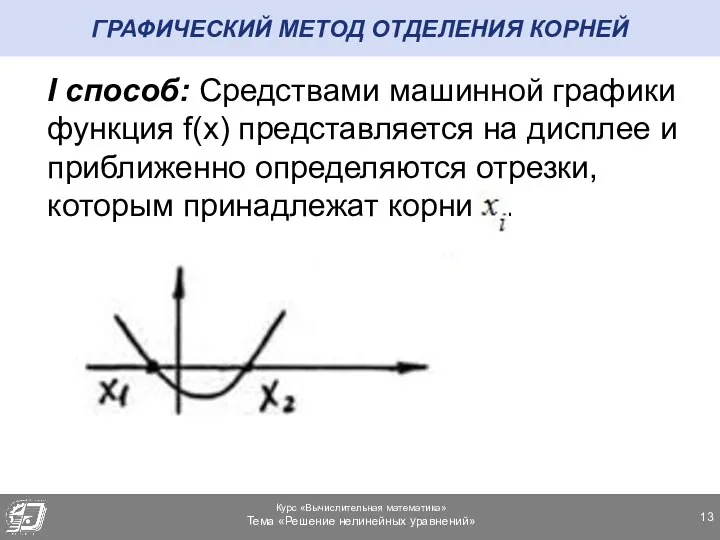
- 13. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ I способ: Средствами машинной графики функция f(x) представляется на дисплее и приближенно
- 14. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ II способ: Все члены уравнения f(x)=0 разбивают на 2 группы, т.е. представляют
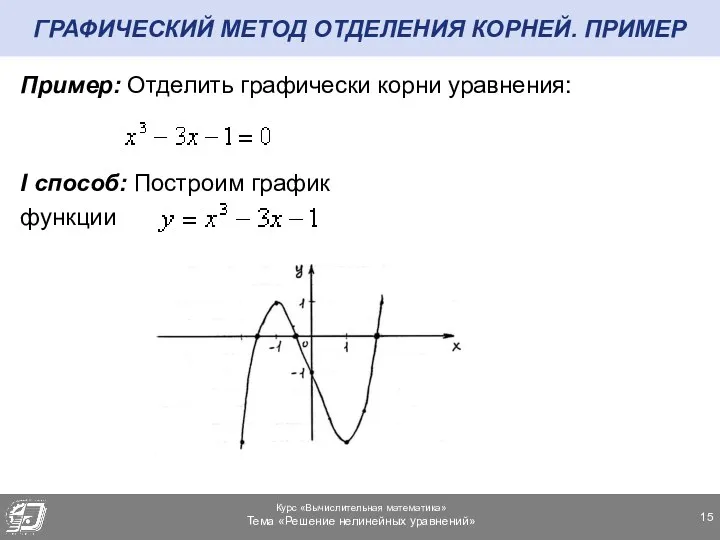
- 15. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР Пример: Отделить графически корни уравнения: I способ: Построим график функции
- 16. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР II способ: Представим данное уравнение в виде и построим графики функций
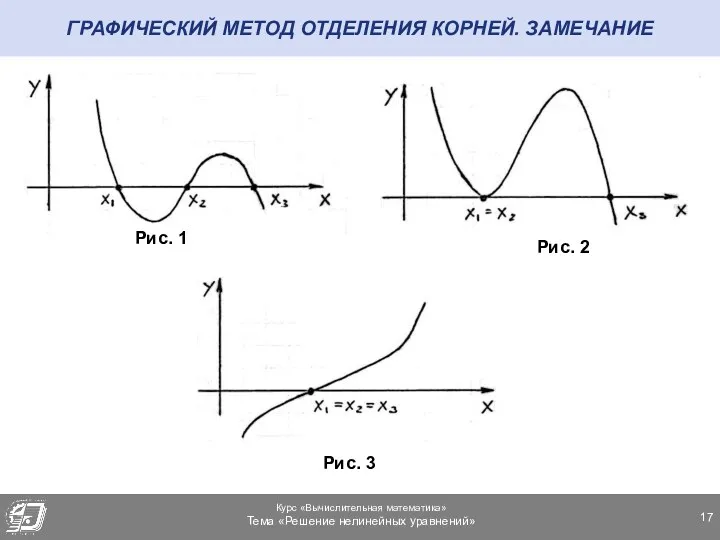
- 17. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ЗАМЕЧАНИЕ Рис. 1 Рис. 2 Рис. 3
- 18. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Аналитически корни уравнения f(x)=0 можно отделить, используя некоторые свойства функций, изучаемые в
- 19. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Теорема 2. Если функция f(x) непрерывна и монотонна на отрезке [a, b]
- 20. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Теорема 3. Если функция f(x) непрерывна на отрезке [a, b] и принимает
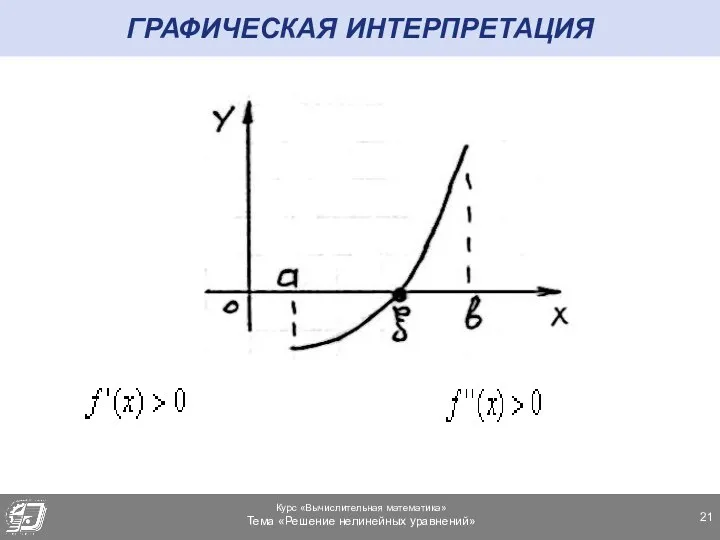
- 21. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
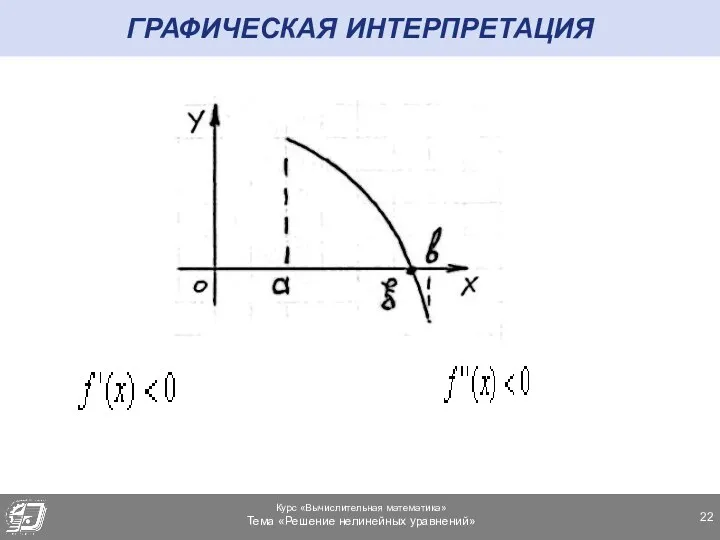
- 22. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
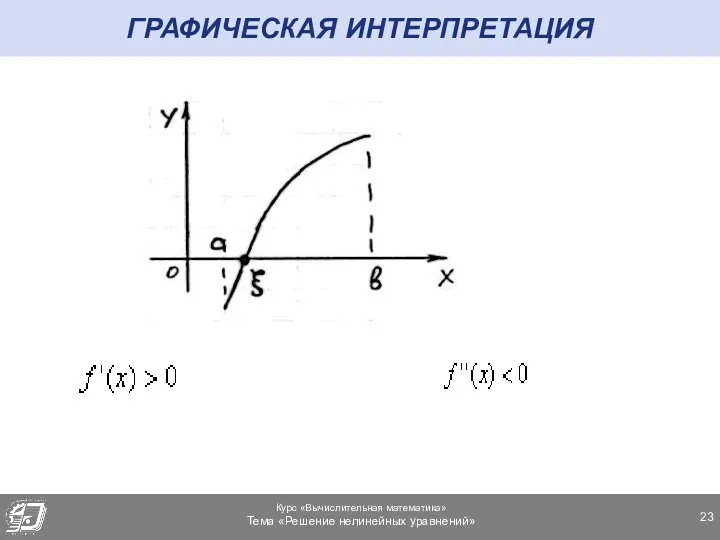
- 23. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
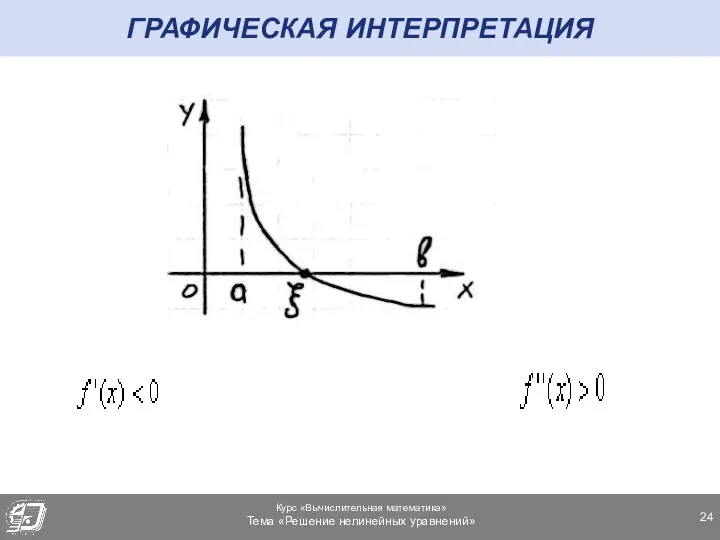
- 24. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
- 25. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Для того чтобы определить наибольшее и наименьшее значение функции на отрезке, надо:
- 26. ПОРЯДОК ДЕЙСТВИЙ ДЛЯ ОТДЕЛЕНИЯ КОРНЕЙ АНАЛИТИЧЕСКИМ МЕТОДОМ 1) Находят f’(x). 2) Составляют таблицу знаков функции f(x),
- 27. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
- 28. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР Составим таблицу знаков функции f(x), полагая х равным: а) критическим значениям
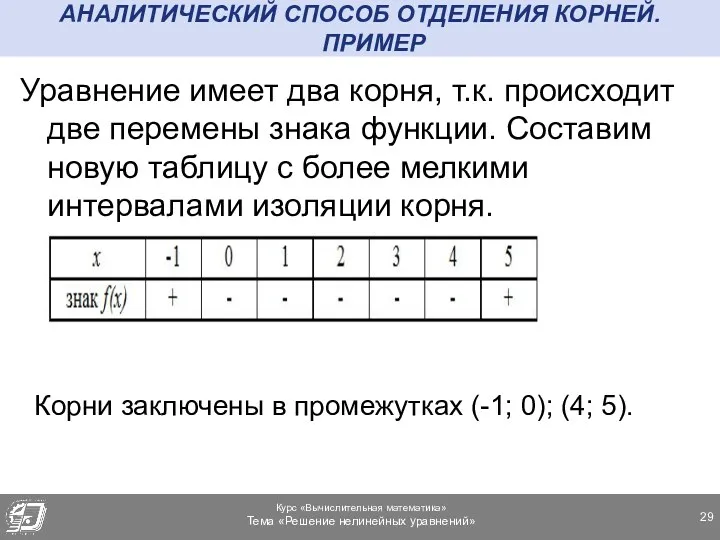
- 29. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР Уравнение имеет два корня, т.к. происходит две перемены знака функции. Составим
- 30. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 1: (о числе корней алгебраического уравнения - действительные числа (1) Алгебраическое
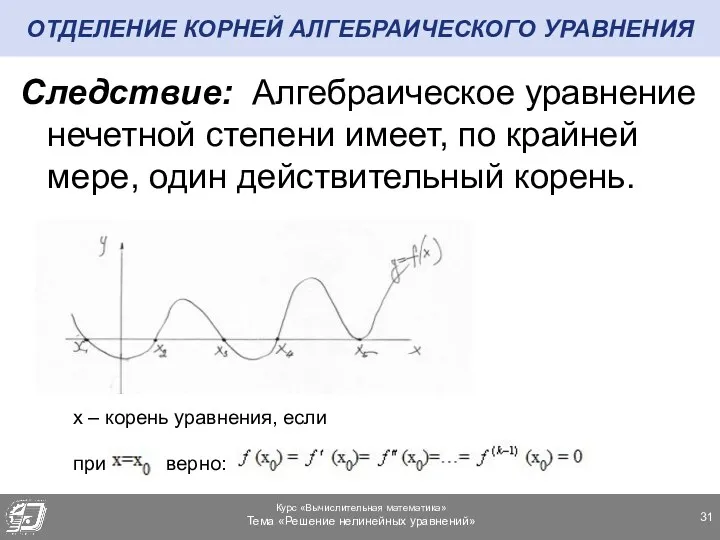
- 31. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Следствие: Алгебраическое уравнение нечетной степени имеет, по крайней мере, один действительный корень.
- 32. КРАТНОСТЬ КОРНЯ Число x есть корень уравнения (1) кратности k, если при x=x0 вместе с функцией
- 33. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
- 34. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 3: (теорема Лагранжа о верхней границе положительных корней уравнения (1)). Пусть
- 35. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 4: (о нижних и верхних границах положительных и отрицательных корней алгебраического
- 36. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Тогда положительные корни и отрицательные корни уравнения(1) удовлетворяют неравенствам:
- 37. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 5: (теорема Декарта о количестве действительных корней алгебраического уравнения). Число S1
- 38. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Число S2 отрицательных корней (с учетом их кратности) алгебраического уравнения равно числу
- 39. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 6: (теорема Гюа о необходимом условии действительности всех корней алгебраического уравнения).
- 40. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР Согласно Следствию Теоремы 1 уравнение имеет 3 корня, среди которых, по
- 41. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР
- 42. ЛОКАЛИЗАЦИЯ ПОЛОЖИТЕЛЬНЫХ КОРНЕЙ
- 43. ЛОКАЛИЗАЦИЯ ПОЛОЖИТЕЛЬНЫХ КОРНЕЙ
- 44. ЛОКАЛИЗАЦИЯ ОТРИЦАТЕЛЬНЫХ КОРНЕЙ Рассчитаем границы отрицательных корней по Теоремам 3 и 4:
- 45. ЛОКАЛИЗАЦИЯ ОТРИЦАТЕЛЬНЫХ КОРНЕЙ
- 46. Нахождение числа положительных корней уравнения Определим количество положительных корней по Теореме 5 уравнения: = Коэффициенты многочлена:
- 47. Нахождение числа отрицательных корней уравнения Определим количество отрицательных корней уравнения. Для уравнения выпишем коэффициенты: -1, -1,
- 48. Исследование структуры корней По Теореме Гюа исследуем структуру корней по коэффициентам уравнения: Необходимое условие действительности всех
- 49. Уточнение корней Уточнение корней – это доведение отделенных корней до заданной степени точности. Второй этап решения
- 50. УТОЧНЕНИЕ КОРНЕЙ Пусть дано уравнение f(x)=0, где f(x) – непрерывная функция. Требуется найти корень этого уравнения
- 51. МЕТОДЫ УТОЧНЕНИЯ КОРНЕЙ 1. МЕТОДЫ ДИХОТОМИИ -Метод половинного деления -Метод хорд 2. Метод простых итераций
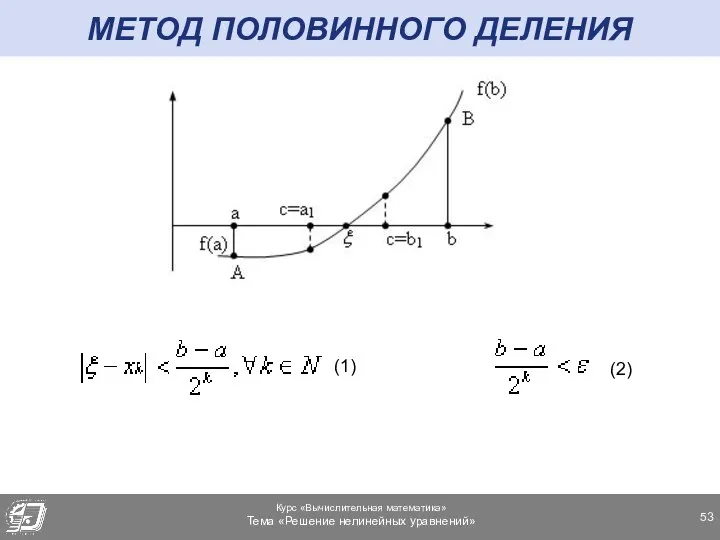
- 52. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ Возьмем на отрезке [a,b] промежуточную точку так, чтобы она являлась серединой отрезка [a,b],
- 53. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (2) (1)
- 54. Априорная оценка метода половинного деления Априорная оценка позволяет предварительно рассчитать примерное количество шагов(итераций), достаточное для получения
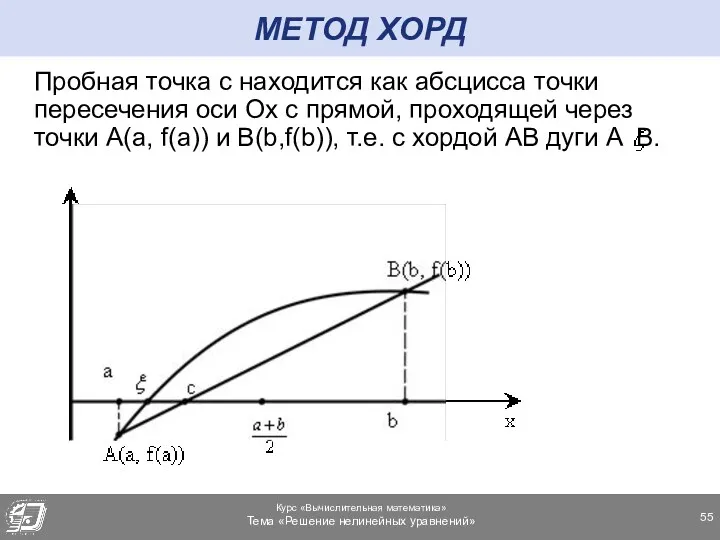
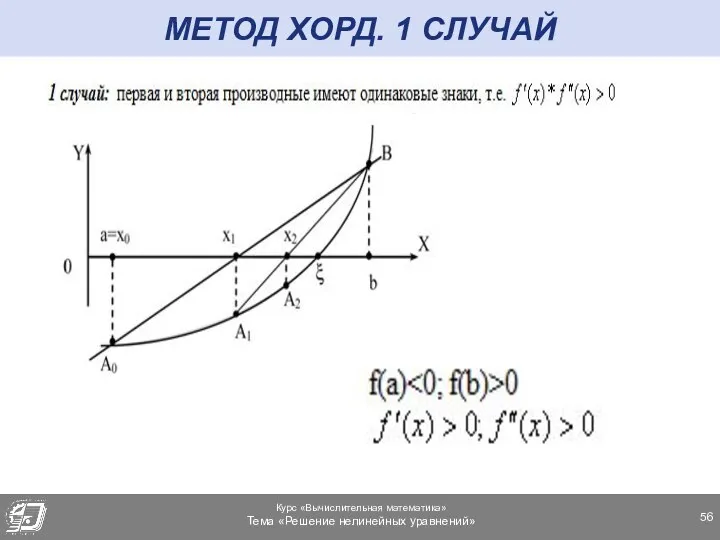
- 55. МЕТОД ХОРД Пробная точка c находится как абсцисса точки пересечения оси Ox с прямой, проходящей через
- 56. МЕТОД ХОРД. 1 СЛУЧАЙ
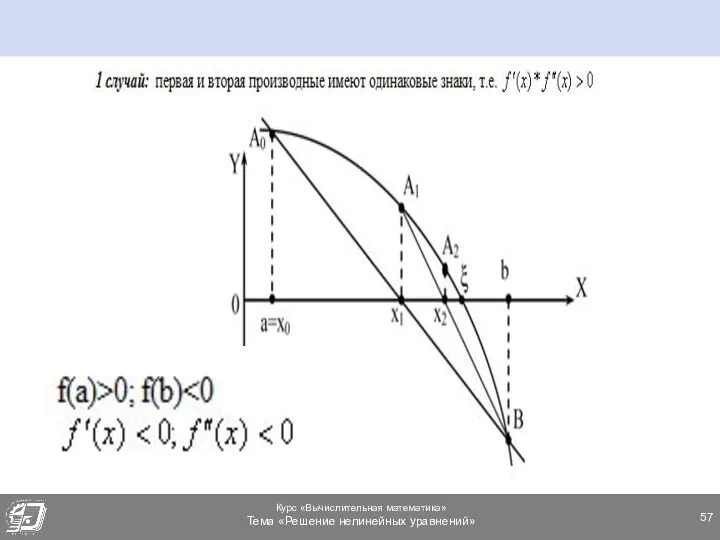
- 58. МЕТОД ХОРД. 1 СЛУЧАЙ
- 59. МЕТОД ХОРД. 1 СЛУЧАЙ (2)
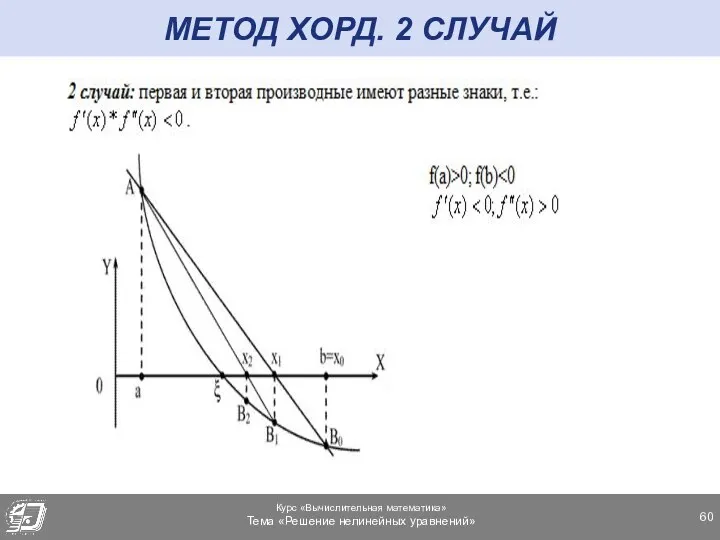
- 60. МЕТОД ХОРД. 2 СЛУЧАЙ
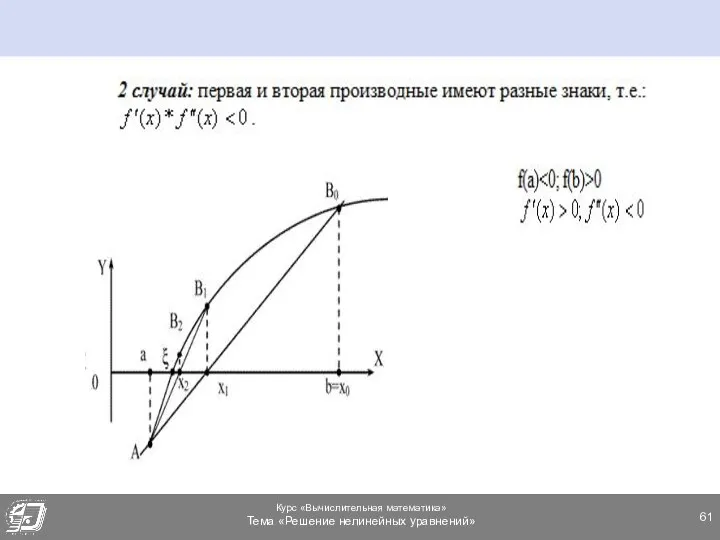
- 62. МЕТОД ХОРД. 2 СЛУЧАЙ
- 63. МЕТОД ХОРД. 2 СЛУЧАЙ В общем случае: (3)
- 64. Выбор формулы (2) или (3) можно осуществить, пользуясь простым правилом: неподвижным концом отрезка является тот, для
- 65. МЕТОД ХОРД → неподвижен конец b, в качестве начального приближения- конец a. При этом используется расчетная
- 66. МЕТОД ХОРД. УСЛОВИЕ ОСТАНОВА ПРОЦЕССА
- 67. МЕТОД ХОРД. УСЛОВИЕ ОСТАНОВА ПРОЦЕССА
- 68. МЕТОД ХОРД. ПРИМЕР
- 69. МЕТОД ХОРД. ПРИМЕР
- 70. МЕТОД ХОРД. ПРИМЕР
- 71. МЕТОД ХОРД. ПРИМЕР
- 72. МЕТОД ХОРД. ПРИМЕР
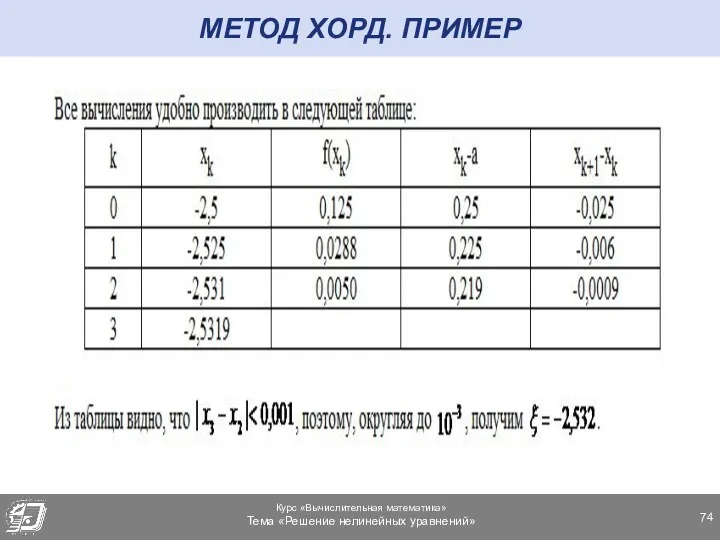
- 73. МЕТОД ХОРД. ПРИМЕР
- 74. МЕТОД ХОРД. ПРИМЕР
- 75. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ Дано (1) (2) Если существует и функция непрерывна, то получим Существование и единственность
- 76. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
- 77. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ [a, b]⊃ [a1, b1]⊃ [a2, b2]⊃… [ak, bk ]⊃… Возрастающая функция
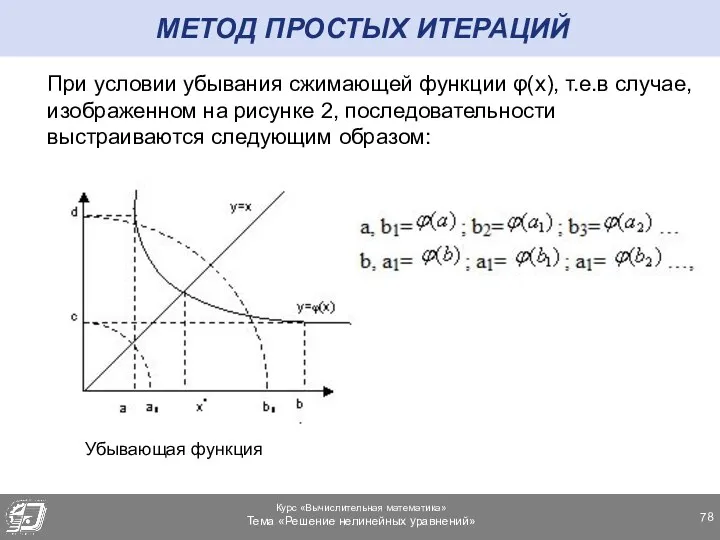
- 78. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ При условии убывания сжимающей функции φ(x), т.е.в случае, изображенном на рисунке 2, последовательности
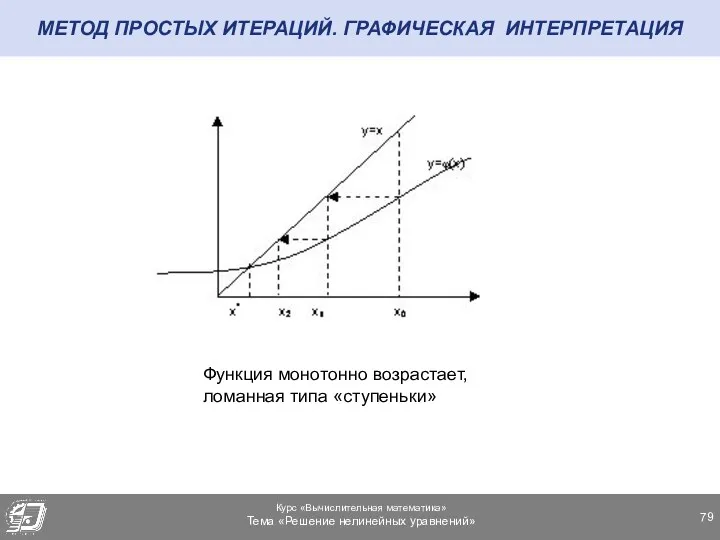
- 79. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ Функция монотонно возрастает, ломанная типа «ступеньки»
- 80. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ Функция монотонно убывает, ломанная типа «спираль»
- 81. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ Выводы: На некотором промежутке [a,b] функция φ(x) удовлетворяет условиям сжатия, зафиксированным в определении
- 82. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
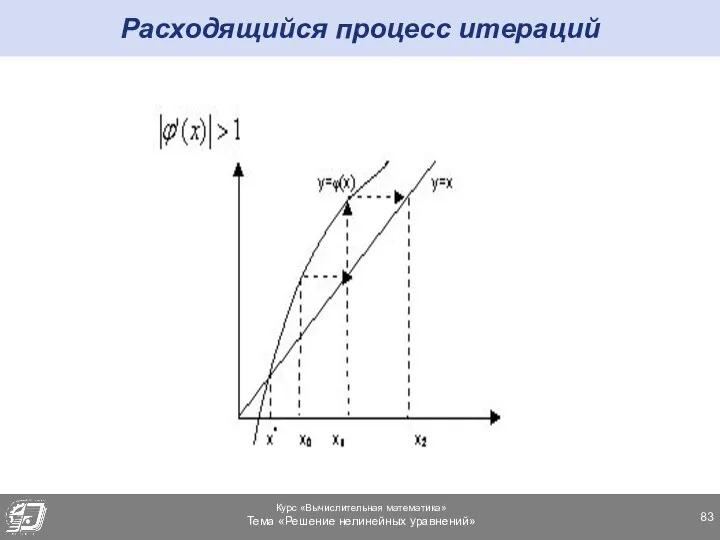
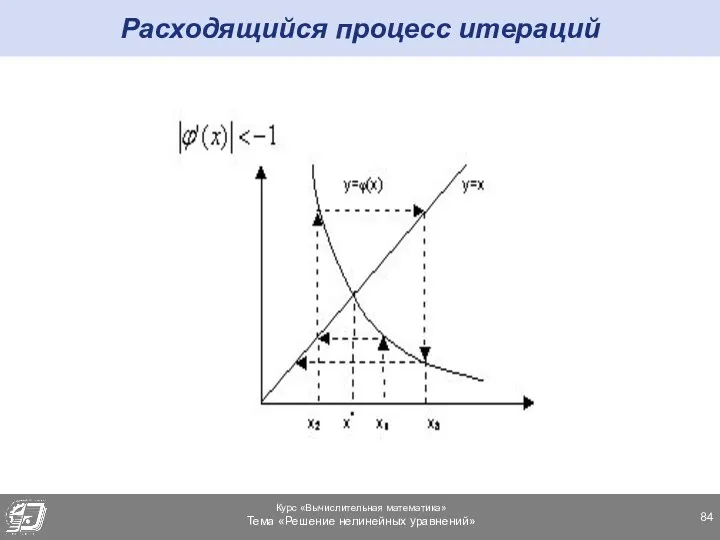
- 83. Расходящийся процесс итераций
- 84. Расходящийся процесс итераций
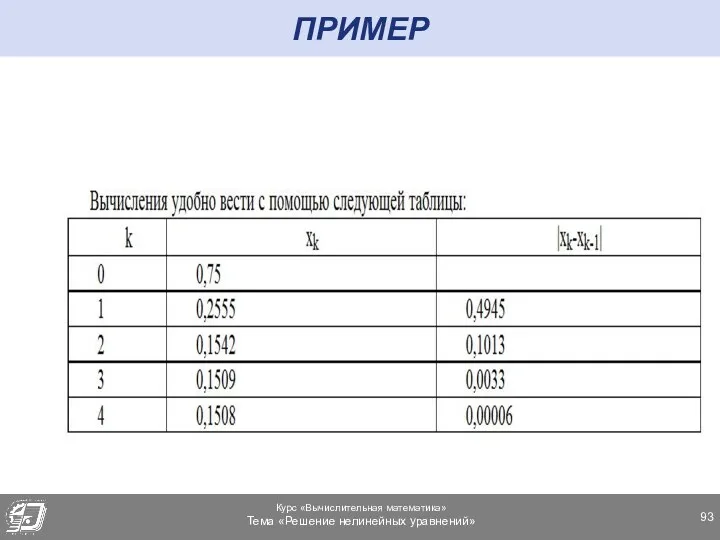
- 85. АПОСТЕРИОРНАЯ ОЦЕНКА Используется для остановки итерационного процесса
- 86. Априорная оценка Используется для предварительного расчета количества операций
- 87. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2) Заменяем f(x)=0 на равносильное x=x+cf(x), c=const≠0 φ(x)=x Находим с
- 88. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2) 2. Заменяем f(x)=0 на равносильное Знак выбирается из условия
- 89. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2) Выражаем x из : f(x)=0 x=φ(x);
- 90. ПРИМЕР
- 91. ПРИМЕР
- 92. ПРИМЕР
- 93. ПРИМЕР
- 95. Скачать презентацию








































![МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ Возьмем на отрезке [a,b] промежуточную точку так,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369169/slide-51.jpg)

















![МЕТОД ПРОСТЫХ ИТЕРАЦИЙ [a, b]⊃ [a1, b1]⊃ [a2, b2]⊃… [ak, bk ]⊃… Возрастающая функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369169/slide-76.jpg)

![МЕТОД ПРОСТЫХ ИТЕРАЦИЙ Выводы: На некотором промежутке [a,b] функция φ(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369169/slide-80.jpg)









 Презентация Вычитание. Название компонентов и результат действия
Презентация Вычитание. Название компонентов и результат действия Функции в жизни человека
Функции в жизни человека Електронний альбом дидактичних матеріалів. Аналітична геометрія у просторі. (Частина 2)
Електронний альбом дидактичних матеріалів. Аналітична геометрія у просторі. (Частина 2) Правила для решения уравнений
Правила для решения уравнений Отношения и их свойства
Отношения и их свойства Шар. Сфера. 11 класс
Шар. Сфера. 11 класс дидактические игры Машины, Шарики
дидактические игры Машины, Шарики Векторы. Средняя линия трапеции. Подготовка к контрольной работе
Векторы. Средняя линия трапеции. Подготовка к контрольной работе Презентация по математике по теме урока: Знакомимся с задачей, 1 класс
Презентация по математике по теме урока: Знакомимся с задачей, 1 класс Основні види переміщення
Основні види переміщення Функция. Свойства функции
Функция. Свойства функции Регрессионный, корреляционный и дисперсионный виды анализа. (Лекция 3)
Регрессионный, корреляционный и дисперсионный виды анализа. (Лекция 3) Устный счёт на уроках математики в пределах 10 (1 класс)
Устный счёт на уроках математики в пределах 10 (1 класс) Конспект урока по математике с презентацией 4 класс по теме Единицы длины. Километр.
Конспект урока по математике с презентацией 4 класс по теме Единицы длины. Километр. Найди пару
Найди пару Решение задач на проценты. Урок математики в 5 классе
Решение задач на проценты. Урок математики в 5 классе Исчисление высказываний. Элементы теории алгоритмов
Исчисление высказываний. Элементы теории алгоритмов Невский проспект Санкт-Петербурга в цифрах. Публичная библиотека в Санкт-Петербурге (часть 6)
Невский проспект Санкт-Петербурга в цифрах. Публичная библиотека в Санкт-Петербурге (часть 6) Умножение. Замена сложения умножением
Умножение. Замена сложения умножением Система организации вагонопотоков. Исходные данные и последовательность составления плана формирования поездов. (Тема 2)
Система организации вагонопотоков. Исходные данные и последовательность составления плана формирования поездов. (Тема 2) Понятие площади многоугольника
Понятие площади многоугольника Мера центральной тенденции. Средние величины и изучение вариации
Мера центральной тенденции. Средние величины и изучение вариации Прямая и обратная пропорциональные зависимости. 6 класс
Прямая и обратная пропорциональные зависимости. 6 класс Умножение одночлена на многочлен
Умножение одночлена на многочлен Квадратичная функция, её свойства и график
Квадратичная функция, её свойства и график Прямоугольный треугольник
Прямоугольный треугольник Перенос графика функции у=ах2 вдоль осей координат
Перенос графика функции у=ах2 вдоль осей координат Геометрические фигуры. Треугольник
Геометрические фигуры. Треугольник