Содержание
- 2. Виды задач Задачи на движение по воде. Задачи на движение по местности. Задачи на работу. Задачи
- 3. Анализ текста задачи. Составление таблицы - условия. Выбор метода решения. Решение. Интерпретация полученного результата. Этапы работы
- 4. Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь
- 5. Необходимо ответить на вопросы: Сколько участников задачи? Какими величинами характеризуется ситуация? Каково количество ситуаций, в которые
- 6. Задачи на движение по течению и против течения реки Собственная скорость катера Vc Скорость течения реки
- 7. Две ситуации Две строки в таблице Сколько ситуаций в задаче?
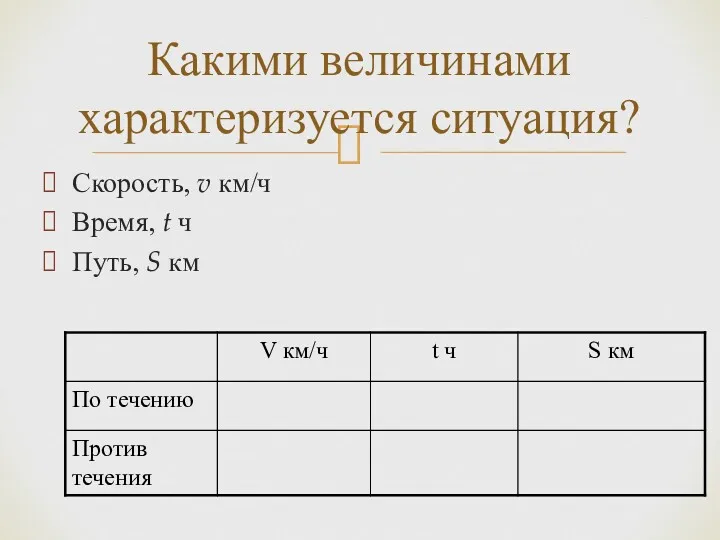
- 8. Скорость, v км/ч Время, t ч Путь, S км Какими величинами характеризуется ситуация?
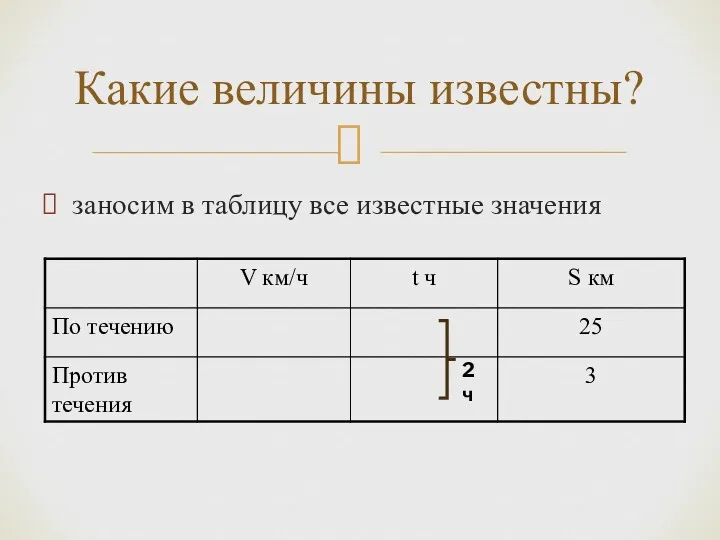
- 9. заносим в таблицу все известные значения Какие величины известны? 2 ч
- 10. заносим в таблицу все связи Пусть х км/ч – скорость лодки в стоячей воде Как связаны
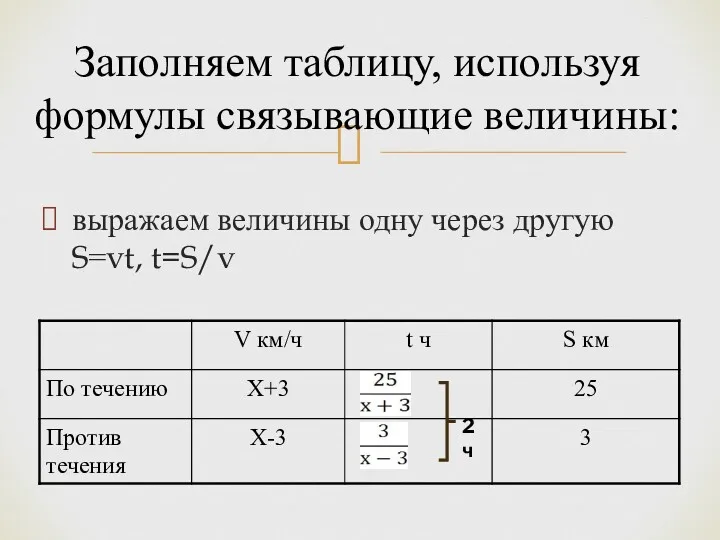
- 11. выражаем величины одну через другую S=vt, t=S/v Заполняем таблицу, используя формулы связывающие величины: 2 ч
- 12. Составление уравнения
- 13. t = s : v 2 км 2 км (х +1) км/ч (х – 1) км/ч
- 14. Катер, собственная скорость которого 8 км/ч, прошёл по реке расстояние, равное 15 км, по течению и
- 15. Решение Известно, что время, затраченное на весь путь, равно 4 ч. Пусть х км/ч – скорость
- 16. Катер отправился в путь в 15 часов, прошел 7км против течения реки и сделал остановку на
- 17. Катер отправился в путь в 15 часов, прошел 7км против течения реки и сделал остановку на
- 18. s – расстояние, v – скорость, t - время s = vt 15 км/ч 10 км/ч
- 19. 20 х – 3 на 3 км/ч меньше х 20 на 3 км/ч больше s –
- 20. Задачи на движение
- 21. Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость
- 22. Первый лыжник прошел расстояние в 20 км на 20 минут быстрее, чем второй. Найдите скорость каждого
- 23. 400км 400км х км/ч (х+20)км/ч Составим уравнение - = 1 Пусть х км/ч скорость товарного поезда
- 24. Задачи на совместную работу
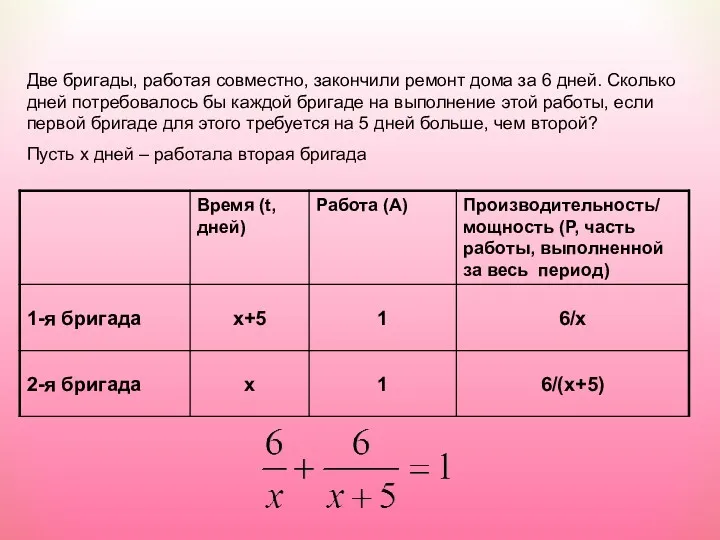
- 25. Две бригады, работая совместно, закончили ремонт дома за 6 дней. Сколько дней потребовалось бы каждой бригаде
- 26. Заказ на 240 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в
- 28. Скачать презентацию







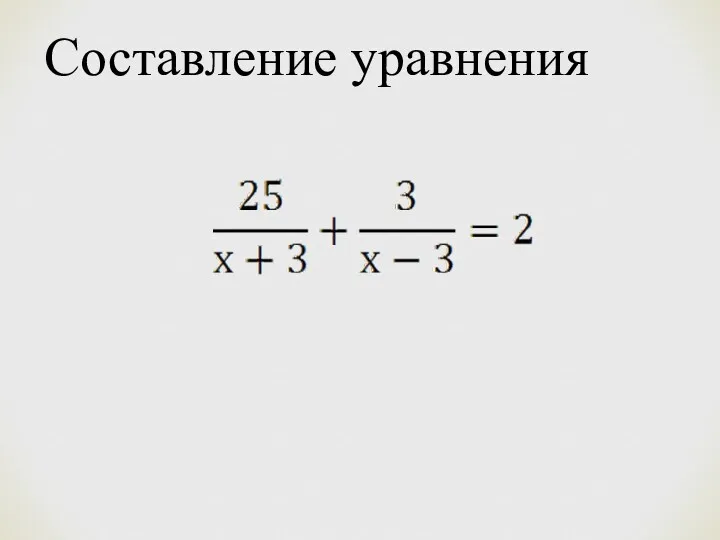












 Значения алгебраической дроби. Совместные действия над алгебраическими дробями
Значения алгебраической дроби. Совместные действия над алгебраическими дробями Магический квадрат
Магический квадрат Задачи для устного счёта по математике
Задачи для устного счёта по математике Основное свойство дроби
Основное свойство дроби Окружающий нас мир – это мир геометрии
Окружающий нас мир – это мир геометрии Розв'язування задач за допомогою рівнянь
Розв'язування задач за допомогою рівнянь Умники и умницы. 8 класс
Умники и умницы. 8 класс Дисперсионный анализ
Дисперсионный анализ Внеклассное занятие .Презентация КВМ ( Клуб весёлых математиков)
Внеклассное занятие .Презентация КВМ ( Клуб весёлых математиков) Числовые характеристики случайных величин. (Тема 5)
Числовые характеристики случайных величин. (Тема 5) Масштаб. Длина окружности и площадь круга
Масштаб. Длина окружности и площадь круга Изображение точек на координатной плоскости
Изображение точек на координатной плоскости Бесінші нөмір
Бесінші нөмір Квадратичная функция и ее график. Урок алгебры. 9 класс
Квадратичная функция и ее график. Урок алгебры. 9 класс Задачи на движение. (6 класс)
Задачи на движение. (6 класс) Средние величины и показатели вариации
Средние величины и показатели вариации Сравниваем двузначные числа
Сравниваем двузначные числа Вычисление площадей фигур на клетчатой бумаге. Формула Пика
Вычисление площадей фигур на клетчатой бумаге. Формула Пика Математика.Тема урока: Числа от 1 до 10.
Математика.Тема урока: Числа от 1 до 10. Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 2
Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 2 Уравнение окружности (9 класс)
Уравнение окружности (9 класс) Презентация к уроку математики решение задач
Презентация к уроку математики решение задач Закрепление изученного
Закрепление изученного Упростите выражение
Упростите выражение Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Количественный счет (презентация)
Количественный счет (презентация) Смежные и вертикальные углы
Смежные и вертикальные углы Центральная симметрия
Центральная симметрия