Содержание
- 2. мода медиана унимодальное и бимодальное распределения взвешенное среднее моменты распределения асимметрия (skewness) эксцесс
- 3. ЗР исчерпывающе описывают СВ и позволяют рассчитать вероятности любых связанных с ними событий Однако: 1) Не
- 4. Числовые характеристики [ распределения ] случайной величины – числа, характеризующие наиболее существенные черты распределения Теоретические –
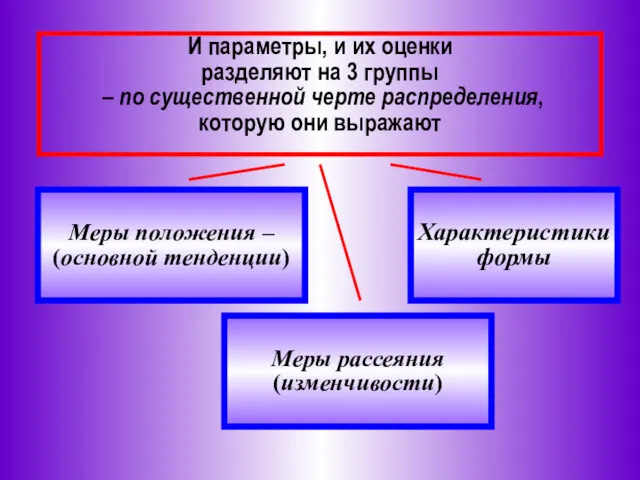
- 5. И параметры, и их оценки разделяют на 3 группы – по существенной черте распределения, которую они
- 6. Фиксируют место СВ на числовой оси. Это некоторое среднее значение, эталон, место нахождения, вокруг которого группируются
- 7. Математическое ожидание дискретной величины есть сумма произведений всех ее значений на вероятности этих значений Другие обозначения
- 8. Примеры М.о. числа очков, выбиваемых 1-ым стрелком: М(X) = 1 ⋅ 0.0 + 2 ⋅ 0.2
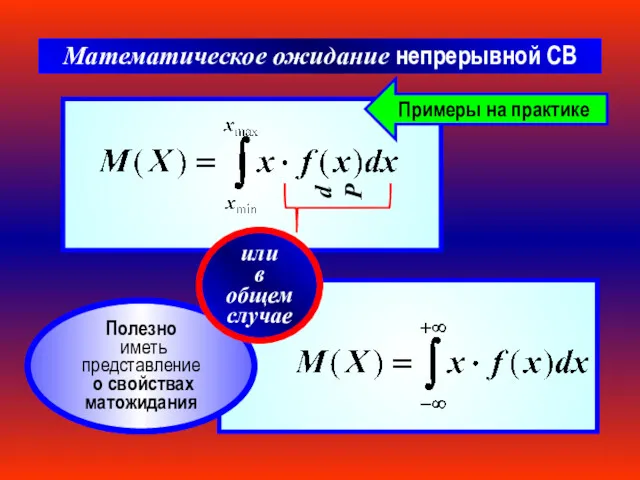
- 9. Математическое ожидание непрерывной СВ dP Примеры на практике Полезно иметь представление о свойствах матожидания или в
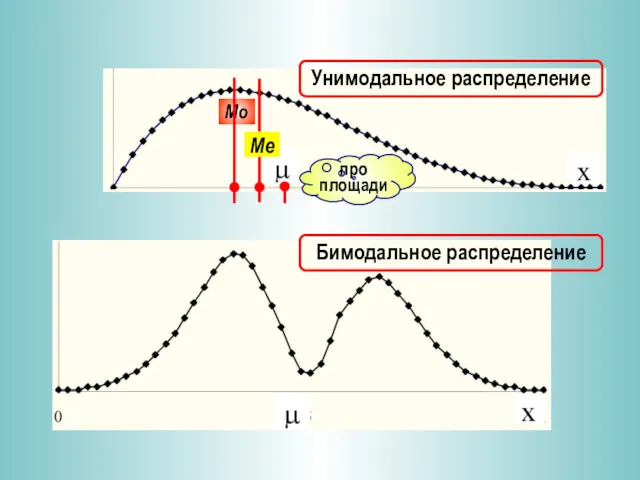
- 10. Mo – значение величины X, которому соответствует максимальная плотность распределения. Для дискретной X – наиболее вероятное
- 11. Унимодальное распределение Бимодальное распределение про площади
- 12. Рассмотрели характеристики центра: Рассматриваем характеристики рассеяния − разброса, изменчивости, вариации матожидание М или μ моду Мо
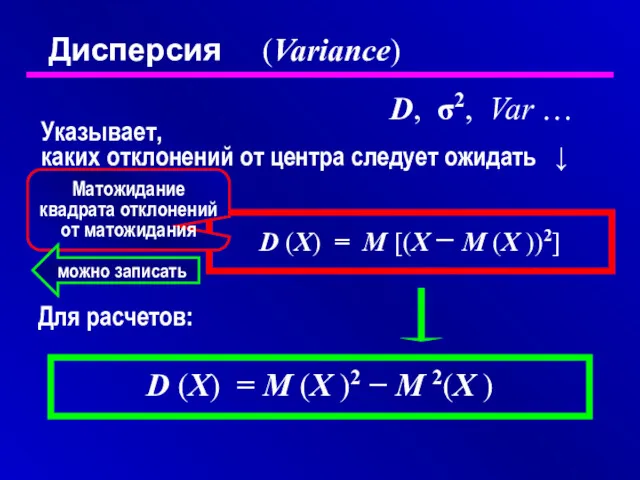
- 13. Дисперсия (Variance) D, σ2, Var … Указывает, каких отклонений от центра следует ожидать ↓ D (X)
- 14. Дисперсия дискретной СВ: Дисперсия непрерывной СВ:
- 15. Был пример про стрелков: значения дисперсии показали − 1-ый стреляет «кучнее», у него разброс попаданий меньше
- 16. Важный пример Применение общей формулы в случае биномиального распределения дает: D = n ⋅ p ⋅
- 17. Пример непрерывной величины Известно, что плотность распределения f(x) = 1/4 в интервале от 40 до 44.
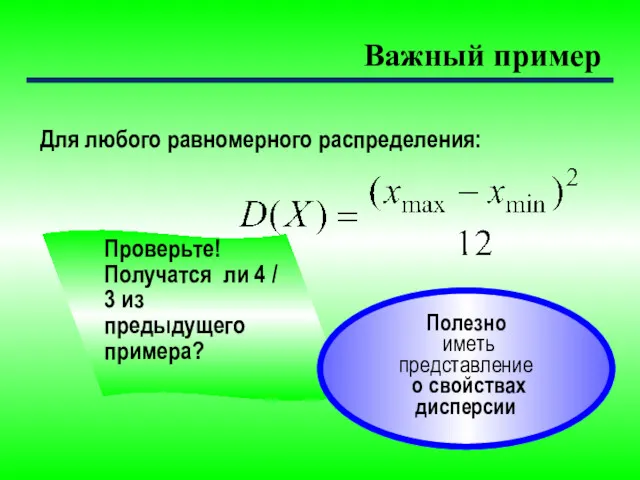
- 18. Важный пример Для любого равномерного распределения: Проверьте! Получатся ли 4 / 3 из предыдущего примера? Полезно
- 19. Более естественная мера разброса ↔ имеет ту же размерность, что и СВ это корень квадратный из
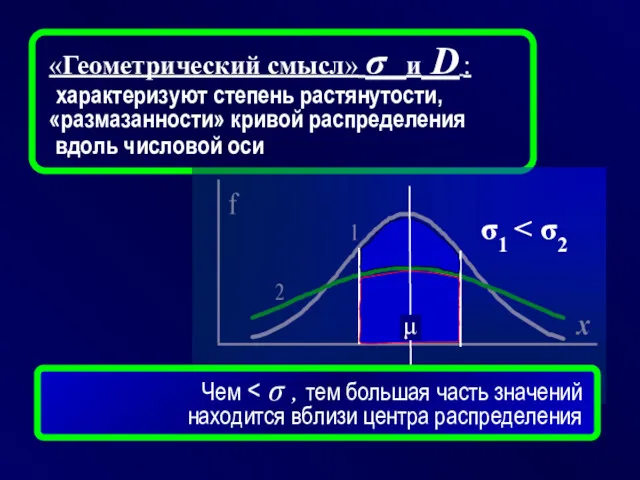
- 20. «Геометрический смысл» σ и D : характеризуют степень растянутости, «размазанности» кривой распределения вдоль числовой оси σ1
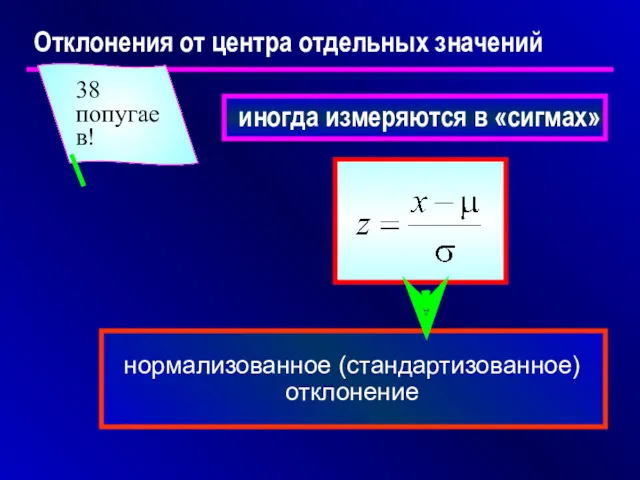
- 21. Отклонения от центра отдельных значений иногда измеряются в «сигмах» нормализованное (стандартизованное) отклонение
- 22. Еще одна характеристика изменчивости коэффициент вариации Мера относительного рассеяния → полезна при сравнении СВ, особенно одних
- 23. Моменты распределения Так называют параметры распределений − по аналогии с механикой Математическое ожидание μ − начальный
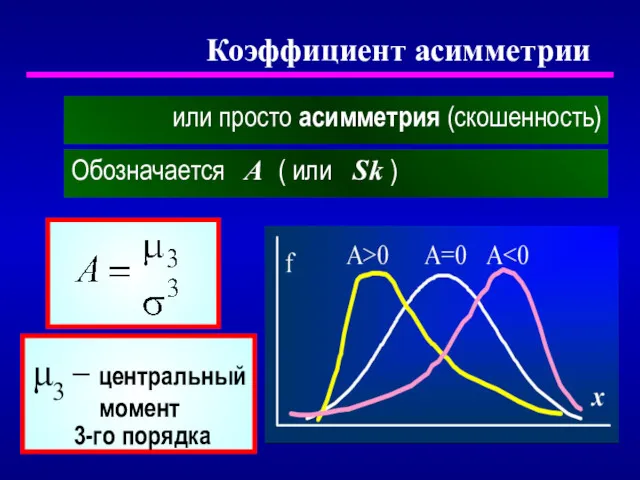
- 24. или просто асимметрия (скошенность) Коэффициент асимметрии Обозначается А ( или Sk ) μ3 − центральный момент
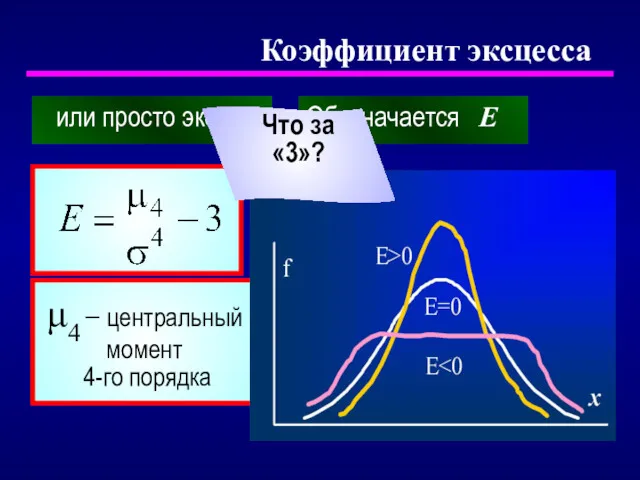
- 25. Коэффициент эксцесса или просто эксцесс Обозначается E μ4 − центральный момент 4-го порядка Что за «3»?
- 27. Скачать презентацию

![Числовые характеристики [ распределения ] случайной величины – числа, характеризующие](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/124671/slide-3.jpg)












 Развитие алгоритмического мышления младших школьников
Развитие алгоритмического мышления младших школьников Математика – царица всех наук. Математическая викторина
Математика – царица всех наук. Математическая викторина Математические диктанты
Математические диктанты Сравнение многозначных чисел.
Сравнение многозначных чисел.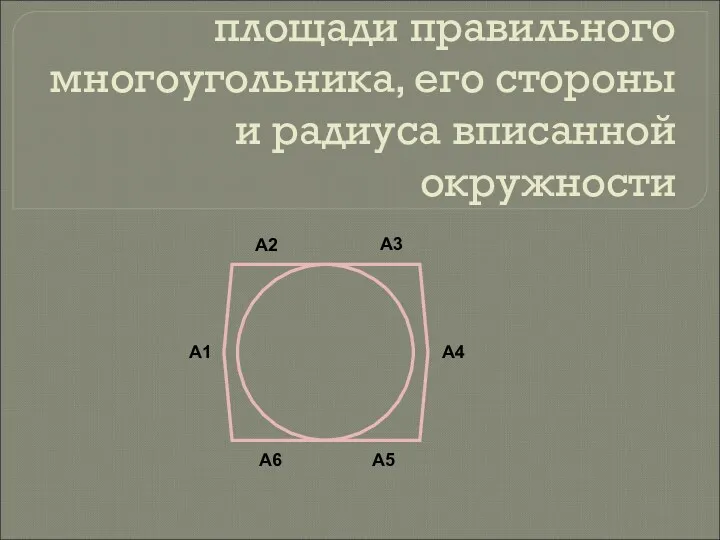 Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Игра Математика в мире животных и животные в мире математики
Игра Математика в мире животных и животные в мире математики Решение задач на нахождение дроби от числа
Решение задач на нахождение дроби от числа Решение задач по теме Некоторые свойства касательных, хорд и секущих в окружности
Решение задач по теме Некоторые свойства касательных, хорд и секущих в окружности Математикадан дидактик уеннар
Математикадан дидактик уеннар Число и цифра 4.
Число и цифра 4. Геометрическая прогрессия
Геометрическая прогрессия Решение заданий С1, С3
Решение заданий С1, С3 Выражение с переменной
Выражение с переменной Объем конуса
Объем конуса Быстро называй ответ
Быстро называй ответ Преобразование графиков тригонометрических функций. Интегрированный урок (математика-информатика)
Преобразование графиков тригонометрических функций. Интегрированный урок (математика-информатика) Решение квадратных неравенств
Решение квадратных неравенств Урок математики
Урок математики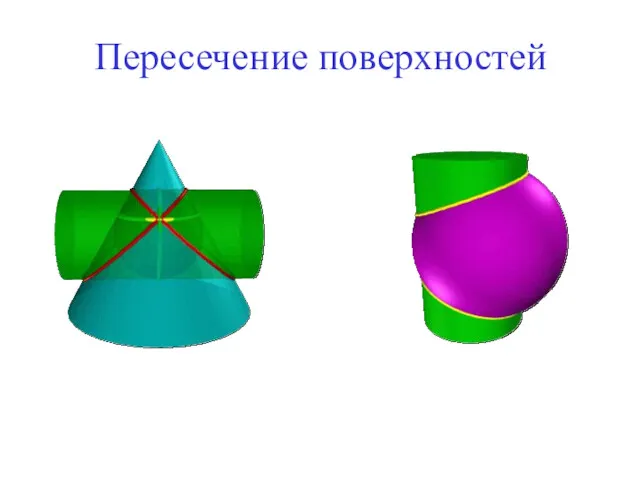 Пересечение поверхностей
Пересечение поверхностей Ряды Фурье
Ряды Фурье Элементы теории нечетких множеств
Элементы теории нечетких множеств Функции y = tgx и y = ctgx, их свойства и графики
Функции y = tgx и y = ctgx, их свойства и графики Интерактивный тренажёр Состав числа 10
Интерактивный тренажёр Состав числа 10 Прямоугольный треугольник
Прямоугольный треугольник Квадрат и куб (1 класс)
Квадрат и куб (1 класс) Графическое представление данных в виде круговых, столбиковых (столбчатых) диаграмм. 7 класс
Графическое представление данных в виде круговых, столбиковых (столбчатых) диаграмм. 7 класс Додавання і множення числових нерівностей. 9 клас
Додавання і множення числових нерівностей. 9 клас Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график