Содержание
- 2. Обчисліть і запишіть в зошит результати: 1.arcsin 2. arccos 3. arctg 5.arcsin (– ) 4. arctg
- 3. До найпростіших тригонометричних рівнянь належать рівняння виду:
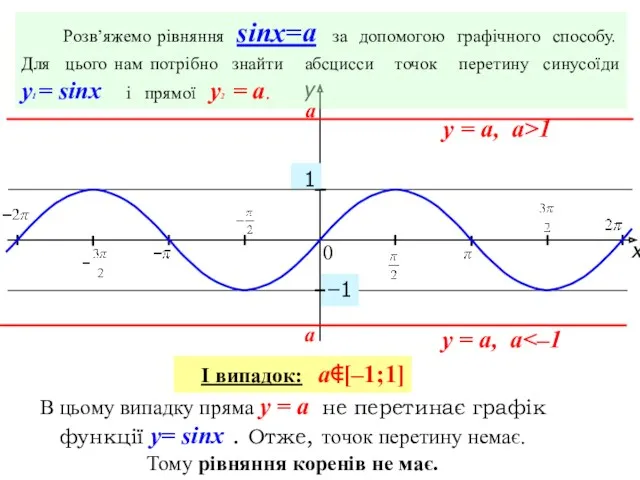
- 4. x y 1 0 −1 Розв’яжемо рівняння sinx=a за допомогою графічного способу. Для цього нам потрібно
- 5. x y 1 0 −1 Очевидно, що в цьому випадку точок перетину безліч, причому їх абсцисси
- 6. x y 1 0 −1 a Отже, всі корені в цьому випадку можна записати у вигляді
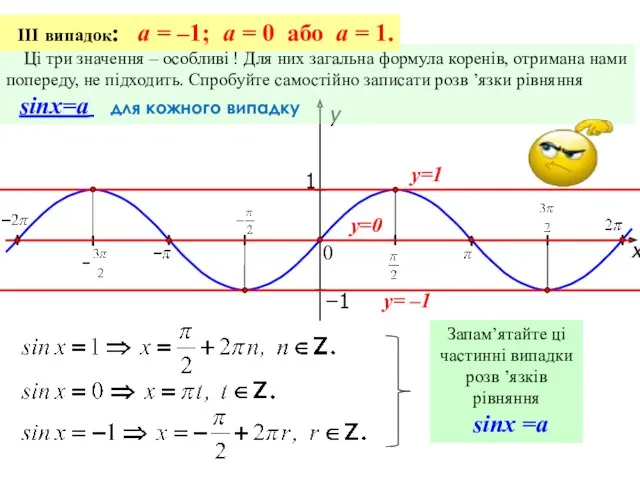
- 7. x y 1 0 −1 Ці три значення – особливі ! Для них загальна формула коренів,
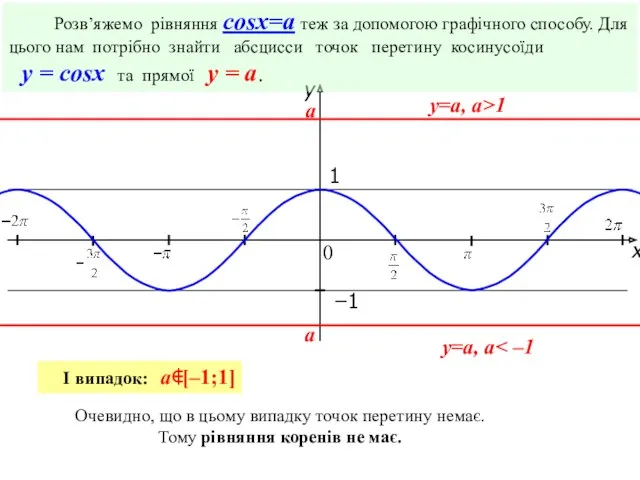
- 8. x y 1 0 −1 Розв’яжемо рівняння cosx=a теж за допомогою графічного способу. Для цього нам
- 9. x y 1 0 −1 II випадок: a∈[–1;1] Очевидно, що в цьому випадку точок перетину безліч,
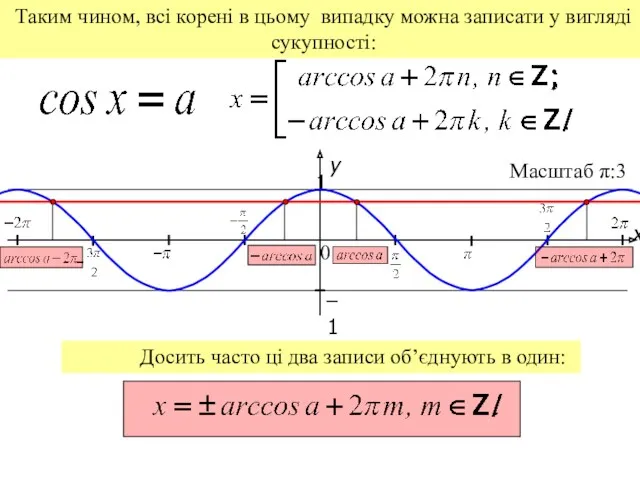
- 10. Таким чином, всі корені в цьому випадку можна записати у вигляді сукупності: Досить часто ці два
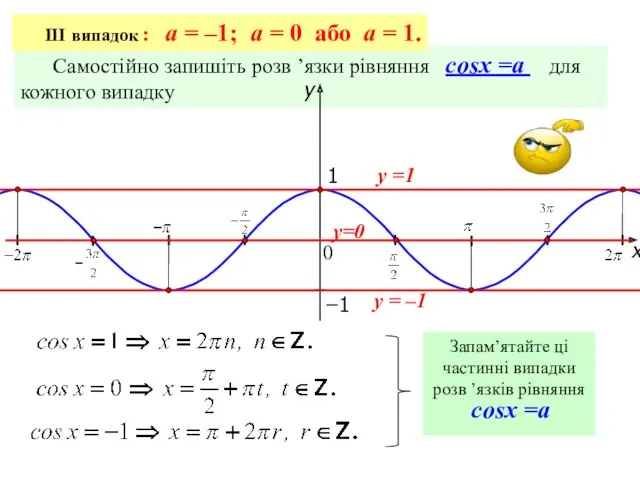
- 11. Самостійно запишіть розв ’язки рівняння cosx =a для кожного випадку III випадок : a = –1;
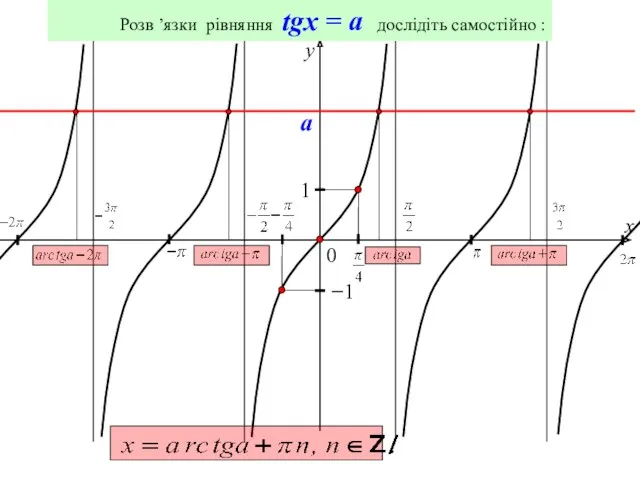
- 12. 0 y 1 x −1 Розв ’язки рівняння tgx = a дослідіть самостійно : a
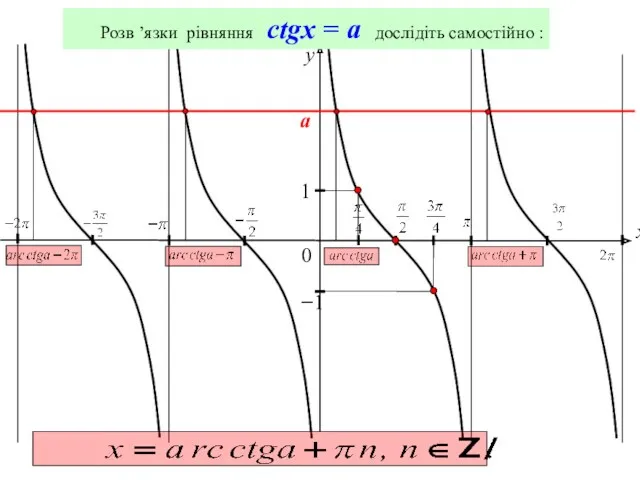
- 13. 0 y 1 x −1 Розв ’язки рівняння сtgx = a дослідіть самостійно : a
- 14. Розв’язання будь-яких тригонометричних рівнянь зводиться до розв’язання найпростіших тригонометричних рівнянь, які ми розглянули вище. Для цього
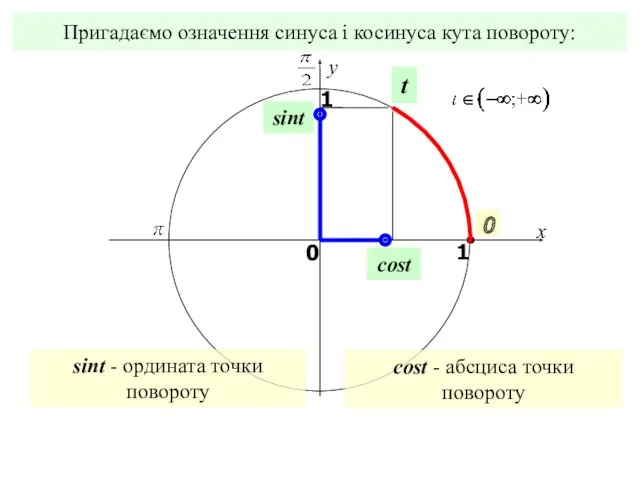
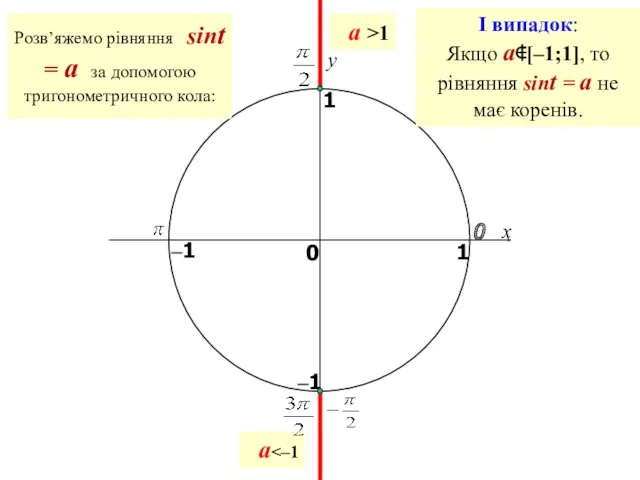
- 15. Пригадаємо означення синуса і косинуса кута повороту: sint cost t x y 0 1 0 1
- 16. x y 0 1 0 1 –1 –1 a >1 a I випадок: Якщо a∉[–1;1], то
- 17. x y 0 1 0 1 t = arcsina t = π –arcsina a –1 –1
- 18. Враховуючи періодичність функції y = sinx (Т=2πn, де n∈Z), кожну з цих точок можна отримати при
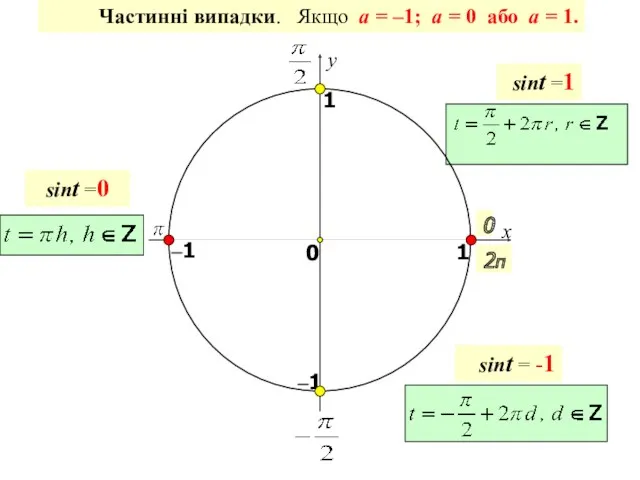
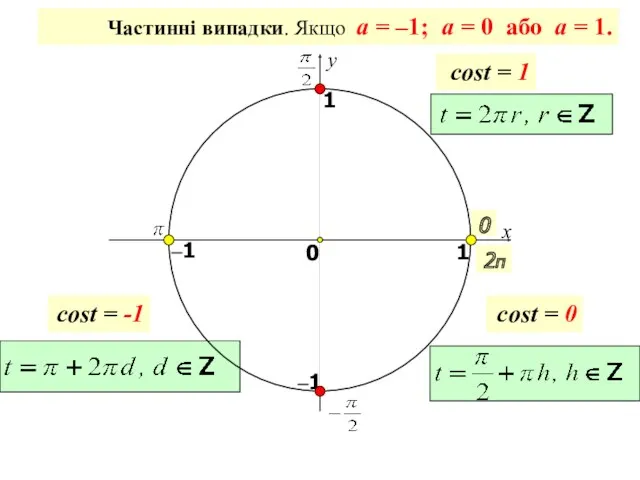
- 19. x y 0 1 0 1 –1 –1 Частинні випадки. Якщо a = –1; a =
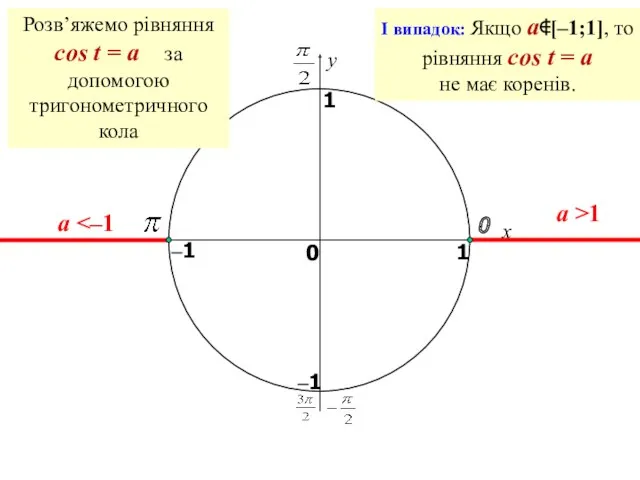
- 20. x y 0 1 0 1 –1 –1 a >1 a I випадок: Якщо a∉[–1;1], то
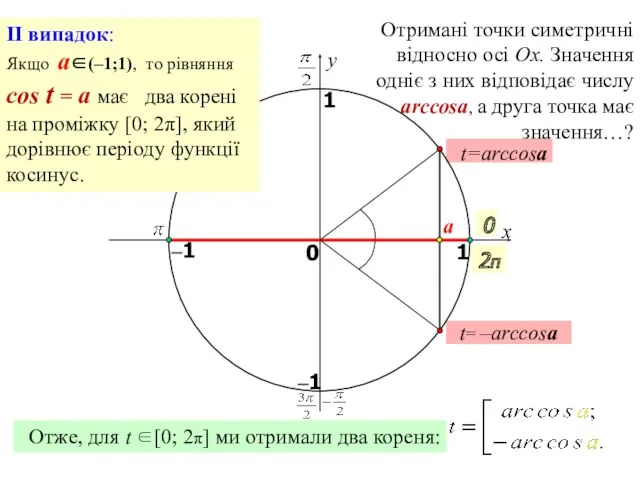
- 21. x y 0 1 0 1 t=arccosa t= –arccosa a –1 –1 II випадок: Якщо a∈(–1;1),
- 22. Враховуючи періодичність функції y = сos x (Т=2πn, де n∈Z), кожну з цих точок можна отримати
- 23. x y 0 1 0 1 –1 –1 2π cost = 1 cost = 0 cost
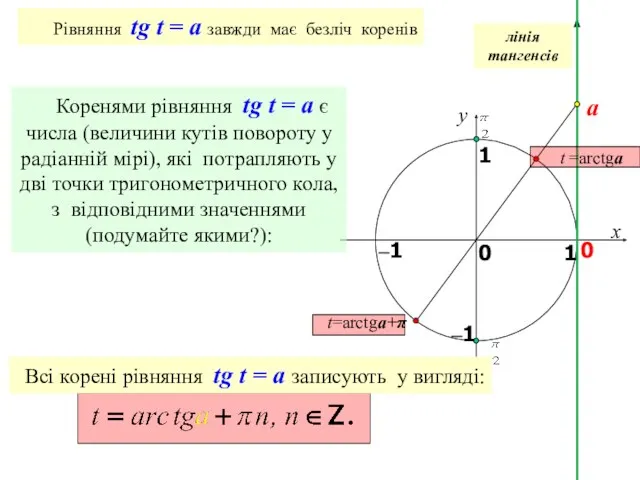
- 24. x y 1 0 1 –1 0 лінія тангенсів a Рівняння tg t = a завжди
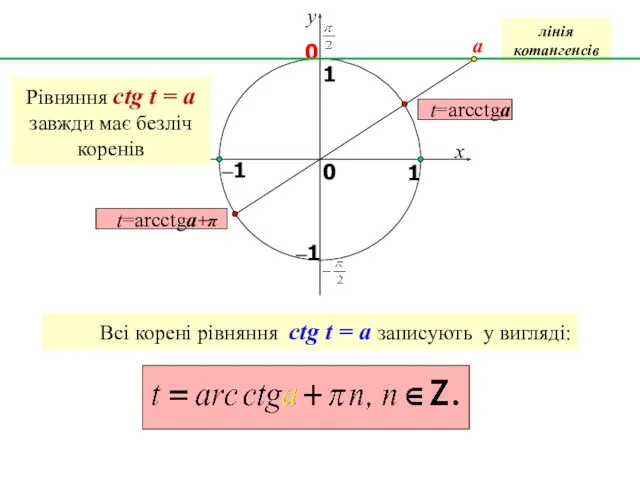
- 25. x y 1 0 1 –1 0 лінія котангенсів a Рівняння сtg t = a завжди
- 26. Формули коренів найпростіших тригонометричних рівнянь 1. cost = а, де |а|≤ 1 або Частинні випадки 1)
- 28. ctg t = a
- 32. Скачать презентацию




![x y 1 0 −1 II випадок: a∈[–1;1] Очевидно, що](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432623/slide-8.jpg)









 Математический досуг Весёлые задачи в форме игры КВН для детей подготовительной группы.
Математический досуг Весёлые задачи в форме игры КВН для детей подготовительной группы. Прямая.Отрезок.Луч
Прямая.Отрезок.Луч Замена произведения чисел их суммой
Замена произведения чисел их суммой Метрологические характеристики средств измерительной техники. Лекция 2
Метрологические характеристики средств измерительной техники. Лекция 2 Микрометр. Определение показаний прибора
Микрометр. Определение показаний прибора Вальс цифр!
Вальс цифр! Математика 4 класс
Математика 4 класс Відсотки. Математика. 6 клас
Відсотки. Математика. 6 клас Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32)
Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32) Угол между векторами. Скалярное произведение векторов. 11 класс
Угол между векторами. Скалярное произведение векторов. 11 класс Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ
Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ Статистические методы в научных исследованиях
Статистические методы в научных исследованиях Мир математики. Игра Счастливый случай
Мир математики. Игра Счастливый случай Трапеция. Виды трапеций
Трапеция. Виды трапеций 20231120_skalyarnoe_proizvedenie_vektorov_v_prostranstve
20231120_skalyarnoe_proizvedenie_vektorov_v_prostranstve Понятие корня n-й степени из действительного числа
Понятие корня n-й степени из действительного числа Открытый банк заданий ОГЭ на подобие треугольников
Открытый банк заданий ОГЭ на подобие треугольников Прогрессия вокруг нас. Заключительный урок. 9 класс
Прогрессия вокруг нас. Заключительный урок. 9 класс Методическое пособие по ФЭМП Какую геометрическую фигуру тебе дать?
Методическое пособие по ФЭМП Какую геометрическую фигуру тебе дать? Отношения a : b
Отношения a : b Создание тренажера по подготовке к ОГЭ по математике
Создание тренажера по подготовке к ОГЭ по математике Презентация Путешествие попугая Кеши по стране Математика Диск
Презентация Путешествие попугая Кеши по стране Математика Диск 3 класс Окружность и круг
3 класс Окружность и круг Дії над векторами у просторі. Розв’язування вправ
Дії над векторами у просторі. Розв’язування вправ Проценты
Проценты Итоговое повторение. Алгебра. 8 класс
Итоговое повторение. Алгебра. 8 класс Умножение и деление
Умножение и деление Математический турнир. Команда Великолепная четвёрка
Математический турнир. Команда Великолепная четвёрка