Содержание
- 2. ЦЕЛИ Познакомиться с историей образования способов нахождения корней линейных и квадратичных многочленов; Понятие многочлена; Схема Горнера;
- 3. НЕМНОГО ИСТОРИИ Способ нахождения корней линейных и квадратичных многочленов, то есть способ решения линейных и квадратных
- 4. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время (следует упомянуть метод, предложенный
- 5. МНОГОЧЛЕНЫ Многочлен от одной переменной x – это выражение вида 〖 a〗_n x^n+a_(n-1) x^(n-1)+⋯+a_1 x+a_0, где
- 6. ЧТО ТАКОЕ СХЕМА ГОРНЕРА? Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена,
- 7. СХЕМА ГОРНЕРА Разберем её на примере После деления многочлена n-ой степени на бином x−a, получим многочлен,
- 8. АЛГОРИТМ РЕШЕНИЯ КУБИЧЕСКОГО УРАВНЕНИЯ Рассмотрим алгоритм решения кубических уравнений, когда x=0 является корнем кубического уравнения Ax3+Bx2+Cx+D=0
- 9. ПРИМЕР РЕШЕНИЯ КУБИЧЕСКИХ УРАВНЕНИЙ Пример. Найти действительные корни уравнения 3x3+4x2+2x=0 Решение. 3x3+4x2+2x=0 x(3x2+4x+2)=0 x=0 является корнем
- 10. АЛГОРИТМ РЕШЕНИЯ БИКВАДРАТНОГО УРАВНЕНИЯ Уравнения вида ax4 + bx2 + c = 0 будем называть биквадратными
- 11. ПРИМЕР РЕШЕНИЯ БИКВАДРАТНОГО УРАВНЕНИЯ Пример. Решить уравнение x4 - 10x2 + 1 = 0 . Решение.
- 12. ТЕОРЕМА БЕЗУ Теорема Безу довольно просто в своем использовании, но при этом она является одной из
- 13. ДОКАЗАТЕЛЬСТВО: Раздели многочлен f(x) на двучлен с остатком r. Получим f(x) =(x-c)*s(c) +r . Теперь подставим
- 14. ИСТОЧНИКИ Биографический словарь деятелей в области математики / сост. Бородин А.И., Бугай А.С. — К.: Рад.
- 16. Скачать презентацию
 Математические правила в стихах
Математические правила в стихах УВЕЛИЧЕНИЕ И УМЕНЬШЕНИЕ ЧИСЛА НА 1
УВЕЛИЧЕНИЕ И УМЕНЬШЕНИЕ ЧИСЛА НА 1 Параллельный перенос
Параллельный перенос Деление трехзначного числа на однозначное. 4 класс
Деление трехзначного числа на однозначное. 4 класс Тест. Итоговое повторение по математике. 4 класс
Тест. Итоговое повторение по математике. 4 класс Ох,уж эта математика! Команды Квадрат и Звезды
Ох,уж эта математика! Команды Квадрат и Звезды Лист Мёбиуса
Лист Мёбиуса Конспект урока по математике для 1 класса, тема: Дециметр, программа - Перспектива
Конспект урока по математике для 1 класса, тема: Дециметр, программа - Перспектива Статистика. Предмет и методы исследования
Статистика. Предмет и методы исследования Линейная функция в физике
Линейная функция в физике Родительское собрание №1. 2021-2022 учебный год
Родительское собрание №1. 2021-2022 учебный год Поверхностные интегралы 1 и 2 рода, их свойства и вычисление. Лекция 29
Поверхностные интегралы 1 и 2 рода, их свойства и вычисление. Лекция 29 Правильные многогранники
Правильные многогранники Сложение векторов. Урок геометрии в 9 классе
Сложение векторов. Урок геометрии в 9 классе Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Правильные многогранники в архитектуре
Правильные многогранники в архитектуре Основания математики. Элементы теории графов
Основания математики. Элементы теории графов Умножение и деление десятичных дробей на 10,100, 1000 и т.д. 5 класс
Умножение и деление десятичных дробей на 10,100, 1000 и т.д. 5 класс Основные теоремы о дифференцируемых функциях, правило Лопиталя. (Лекция 11)
Основные теоремы о дифференцируемых функциях, правило Лопиталя. (Лекция 11)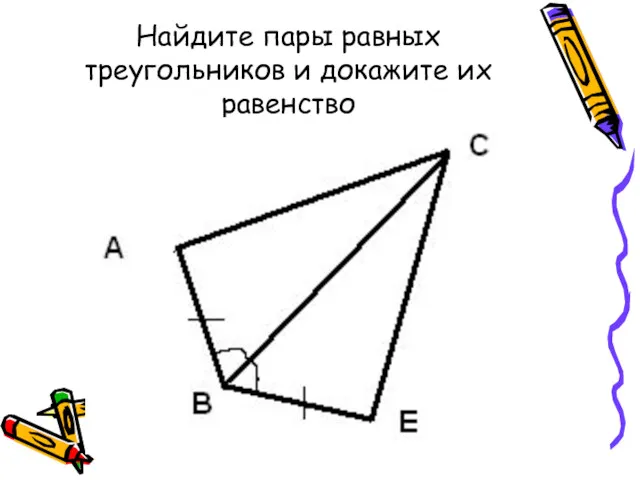 Равнобедренный треугольник
Равнобедренный треугольник Решение линейных неравенств. 8 класс
Решение линейных неравенств. 8 класс Измерение углов
Измерение углов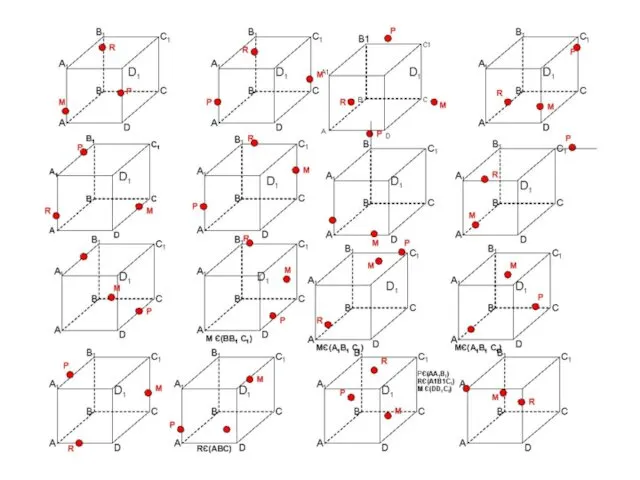 Постороение сечений
Постороение сечений Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Алгебраические выражения. Подготовка к ГИА
Алгебраические выражения. Подготовка к ГИА Сложные проценты
Сложные проценты Презентация к уроку математики 1 класс Таблица сложения
Презентация к уроку математики 1 класс Таблица сложения Письменное умножение на двузначное число
Письменное умножение на двузначное число