Содержание
- 2. Цель лекции – изучить статистические методы анализа данных параметров транспортного процесса. План лекции. Статистические методы анализа
- 3. 1. Статистические методы анализа данных. Статистика изучает большие массивы информации и устанавливает закономерности, которым подчиняются случайные
- 5. В теории статистику принято условно различать на: - описательную - аналитическую. Описательная статистика связана с планированием
- 6. Типовые задачи анализа данных. Одномерный анализ: Сравнение математических ожиданий; Сравнение дисперсий; Оценивание параметров распределений; Установление закона
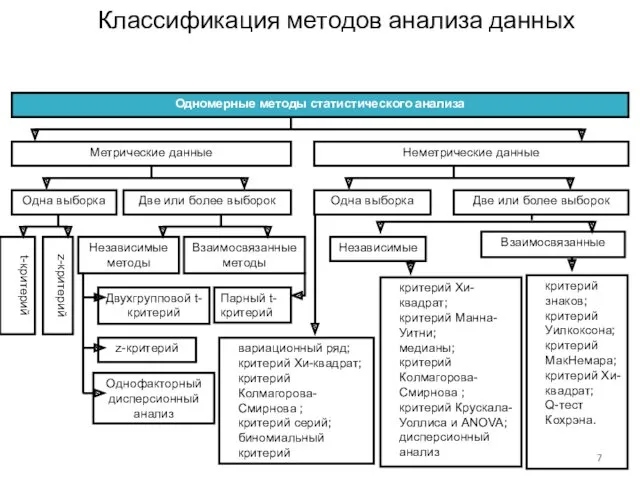
- 7. Классификация методов анализа данных
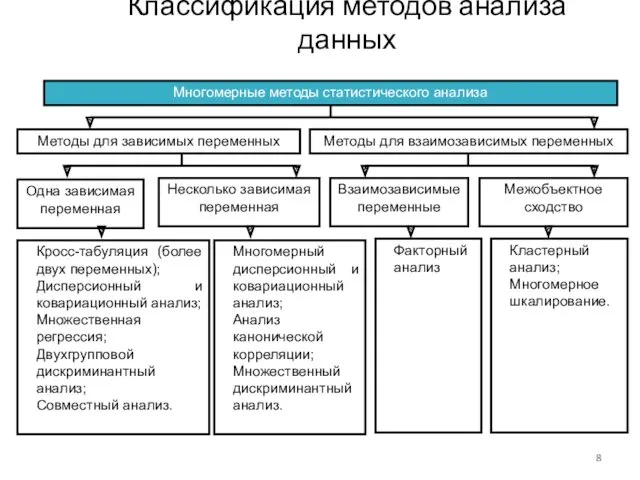
- 8. Классификация методов анализа данных
- 9. Основные задачи статистического анализа: статистическая проверка гипотез; определение числа наблюдений и получение выборки; определение характеристик генеральной
- 10. Способы представления данных Группировка Табулирование Ранжирование Распределение частот Интервальное распределения частот Статистические ряды Графическое представление данных
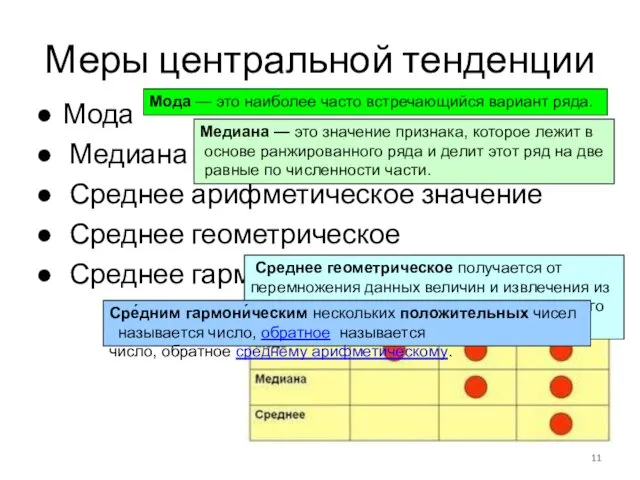
- 11. Меры центральной тенденции Мода Медиана Среднее арифметическое значение Среднее геометрическое Среднее гармоническое Мода — это наиболее
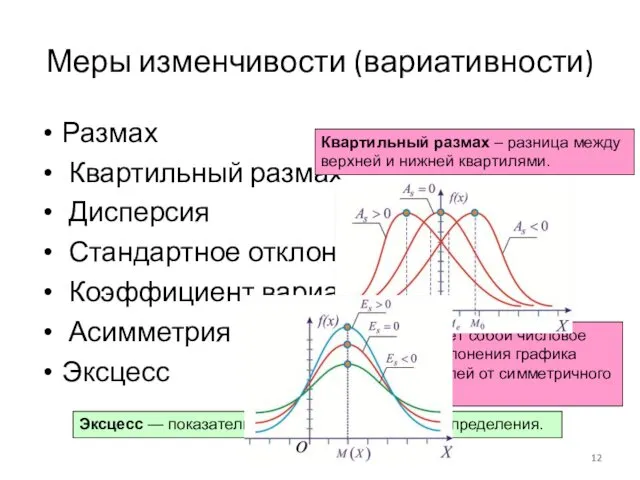
- 12. Меры изменчивости (вариативности) Размах Квартильный размах Дисперсия Стандартное отклонение Коэффициент вариации Асимметрия Эксцесс Квартильный размах –
- 13. Совокупность – группа объектов, предметов или явлений, объединенных каким-либо общим признаком или свойством качественной или количественной
- 14. Характеристики совокупностей
- 15. При проведении выборочного наблюдения необходимо соблюдать следующие требования: единицы совокупности должны быть: легко различимы; на перекрывать
- 16. Процесс построения выборки - из большей по размеру генеральной совокупности извлекается выборка для проведения измерений и
- 17. Для того, чтобы выборка была репрезентативной (хорошо представлять элементы ГС), она должна быть отобрана случайно. Случайность
- 18. Пусть получена выборка объема n. Над этим массивом исходных данных выполняется операция ранжирования, т.е. экспериментальные данные
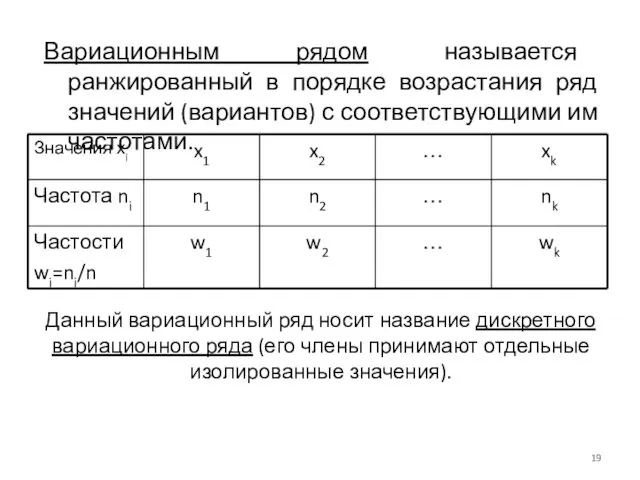
- 19. Данный вариационный ряд носит название дискретного вариационного ряда (его члены принимают отдельные изолированные значения). Вариационным рядом
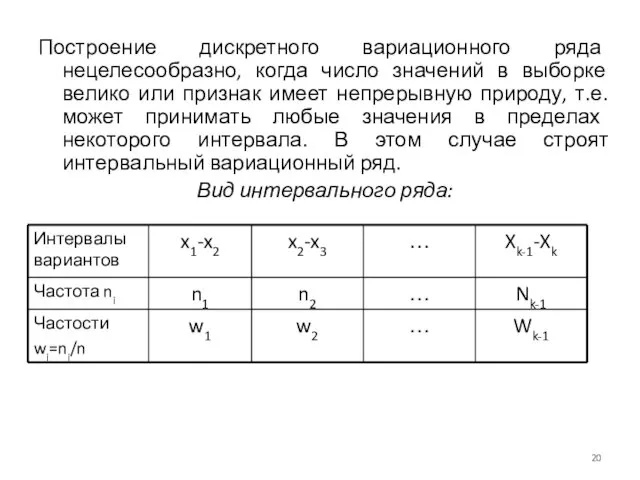
- 20. Построение дискретного вариационного ряда нецелесообразно, когда число значений в выборке велико или признак имеет непрерывную природу,
- 21. Статистический метод определения объема выборки Для бесповторного отбора Для повторного отбора где σ2 – дисперсия генеральной
- 22. Особенность представленных формул : - в первом случае можно вести расчет, отталкиваясь от известного нам объема
- 23. Величина σ2 , характеризующая дисперсию признака в генеральной совокупности, чаще всего бывает неизвестна. Поэтому используют следующие
- 24. 2. Можно использовать данные прошлых выборочных наблюдений, проводившихся в аналогичных целях, т.е. дисперсия, полученная по их
- 25. 2. Методы анализа данных в MS Excel. Программа MS Excel обладает: специальным набором функций, которые позволяют
- 26. Файл MS Excel представляет собой книгу, которая состоит из набора листов. Каждый лист представляет собой таблицу
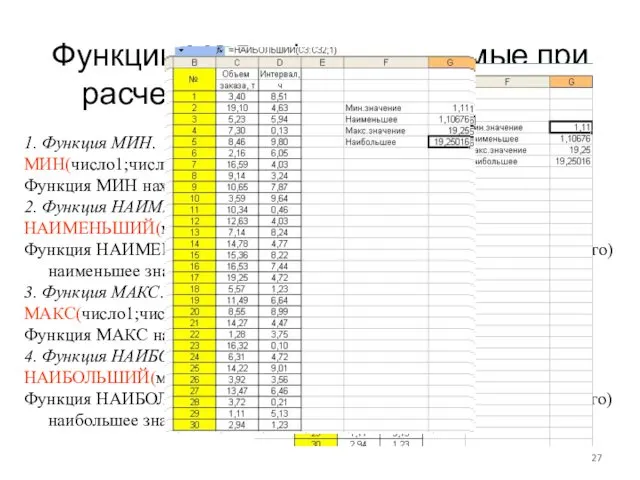
- 27. Функции MS Excel, используемые при расчете показателей положения 1. Функция МИН. МИН(число1;число2;…). Функция МИН находит наименьшее
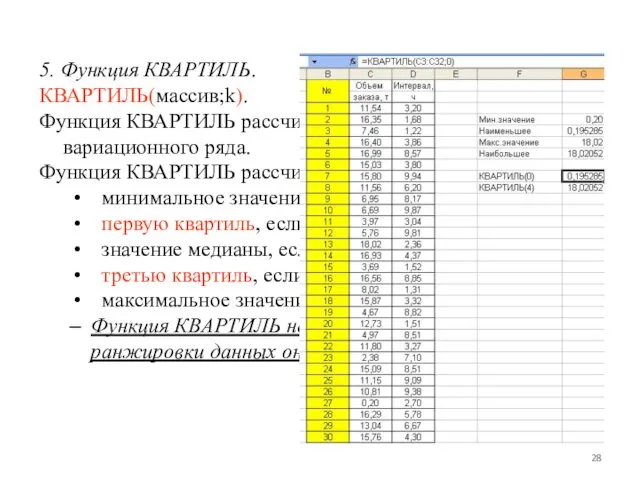
- 28. 5. Функция КВАРТИЛЬ. КВАРТИЛЬ(массив;k). Функция КВАРТИЛЬ рассчитывает квартиль дискретного вариационного ряда. Функция КВАРТИЛЬ рассчитывает: минимальное значение,
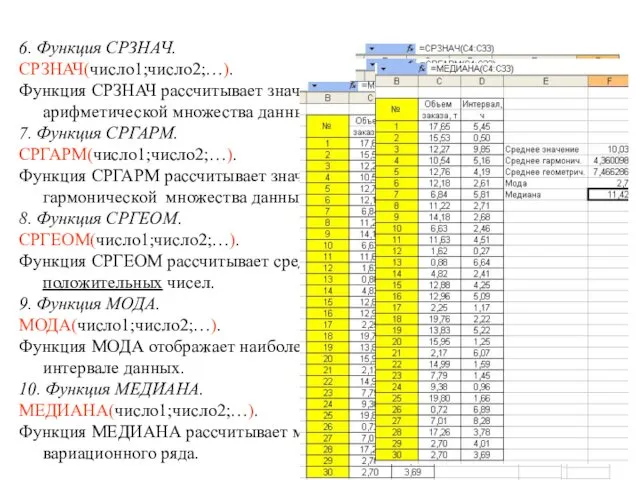
- 29. 6. Функция СРЗНАЧ. СРЗНАЧ(число1;число2;…). Функция СРЗНАЧ рассчитывает значение невзвешенной средней арифметической множества данных. 7. Функция СРГАРМ.
- 30. Функции MS Excel, используемые при расчете показателей разброса 1. Функция ДИСП. ДИСП(число1;число2;…). Функция ДИСП оценивает генеральную
- 31. 3. Функция СТАНДОТКЛОН. СТАНДОТКЛОН(число1;число2;…). Функция СТАНДОТКЛОН оценивает генеральное стандартное отклонение (стандарт) по выборке. Функция СТАНДОТКЛОН рассчитывает
- 32. Функция Excel, используемая при расчете показателя асимметрии Функция СКОС. СКОС(число1;число2;…). Функция СКОС оценивает коэффициент асимметрии по
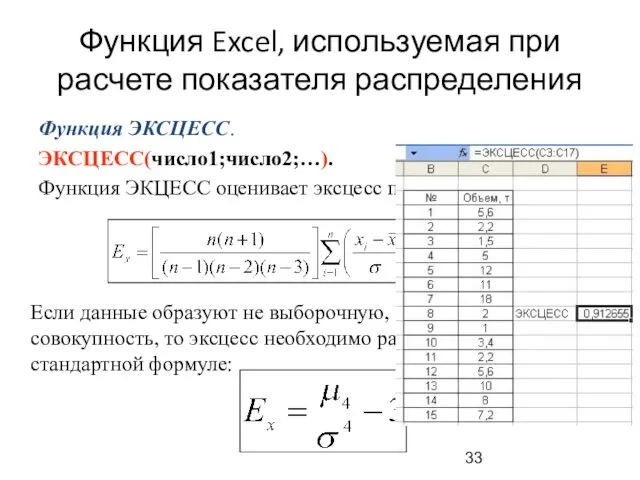
- 33. Функция Excel, используемая при расчете показателя распределения Функция ЭКСЦЕСС. ЭКСЦЕСС(число1;число2;…). Функция ЭКЦЕСС оценивает эксцесс по выборке
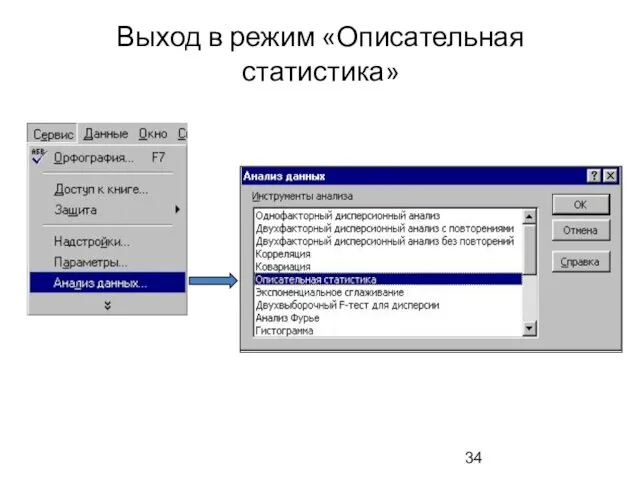
- 34. Выход в режим «Описательная статистика»
- 35. Справочная информация по технологии работы в режиме «Описательная статистика»
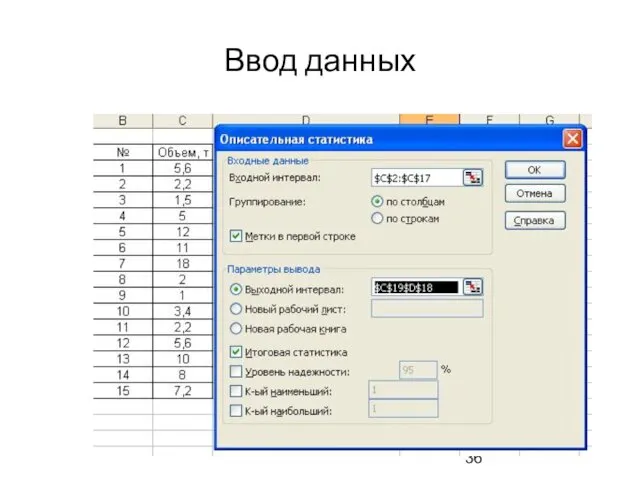
- 36. Ввод данных
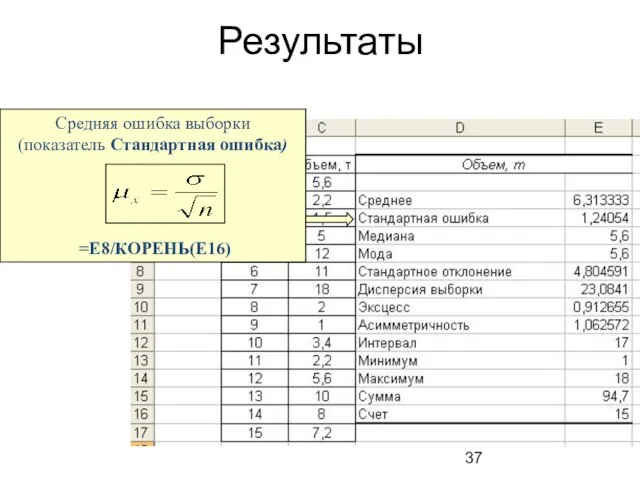
- 37. Результаты
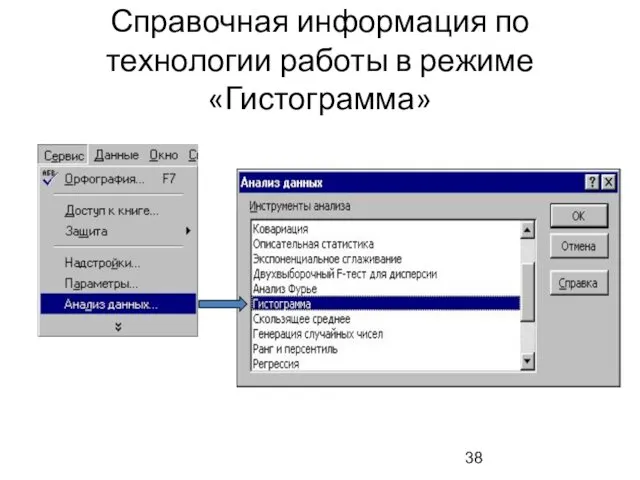
- 38. Справочная информация по технологии работы в режиме «Гистограмма»
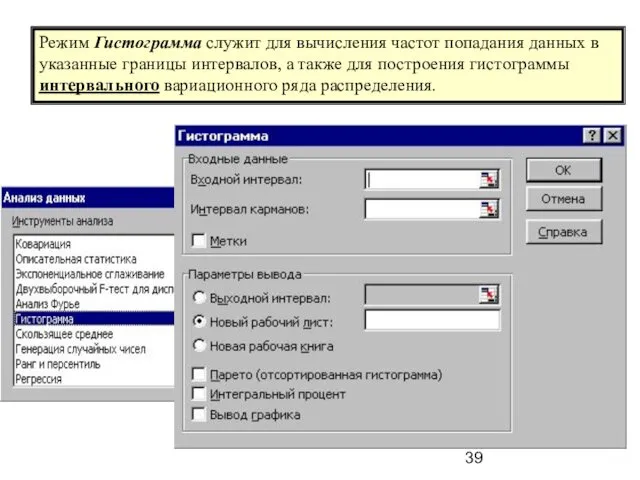
- 39. Режим Гистограмма служит для вычисления частот попадания данных в указанные границы интервалов, а также для построения
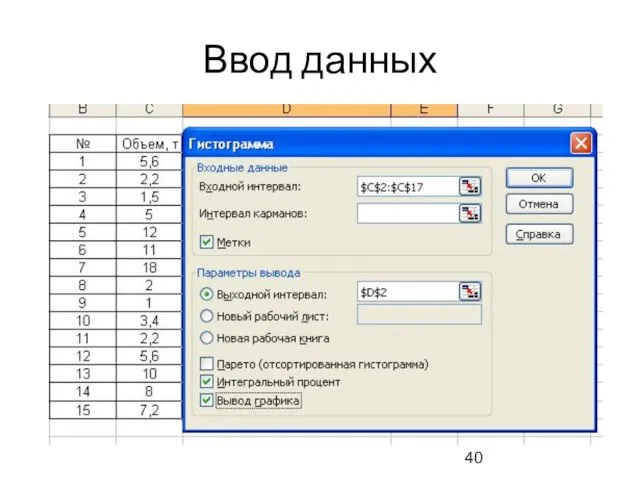
- 40. Ввод данных
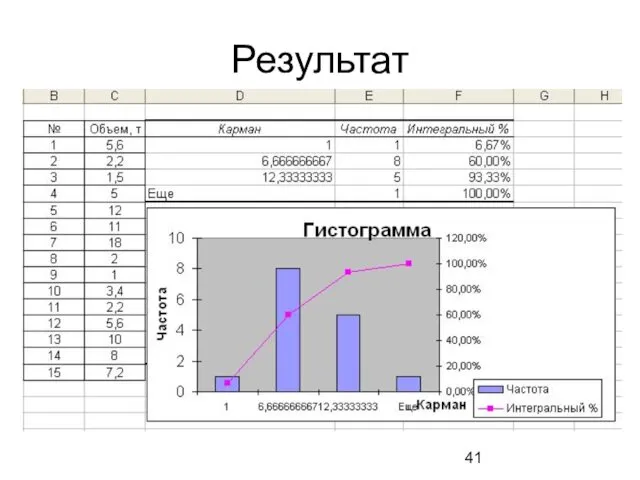
- 41. Результат
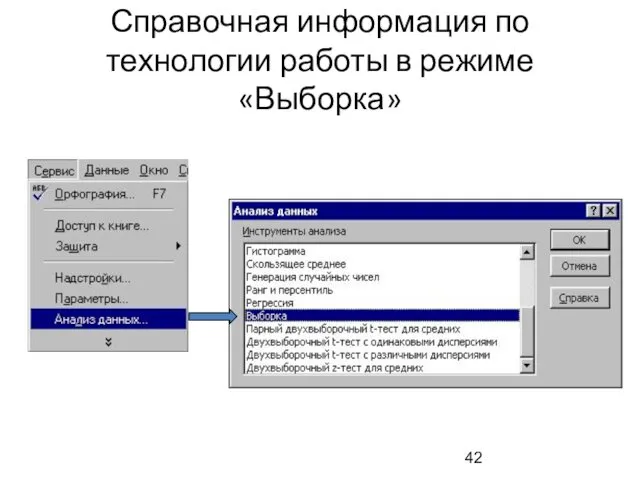
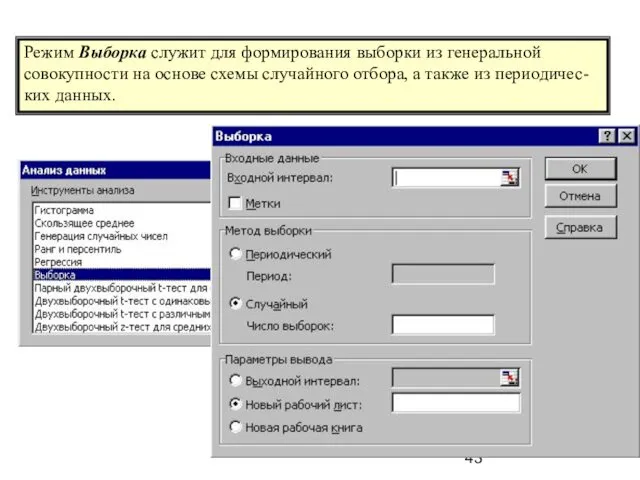
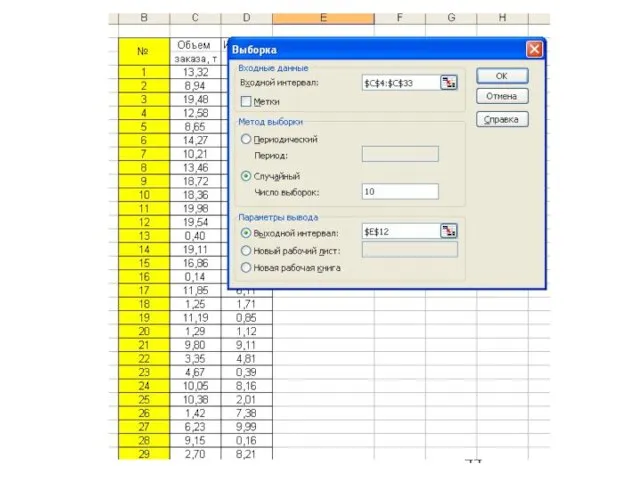
- 42. Справочная информация по технологии работы в режиме «Выборка»
- 43. Режим Выборка служит для формирования выборки из генеральной совокупности на основе схемы случайного отбора, а также
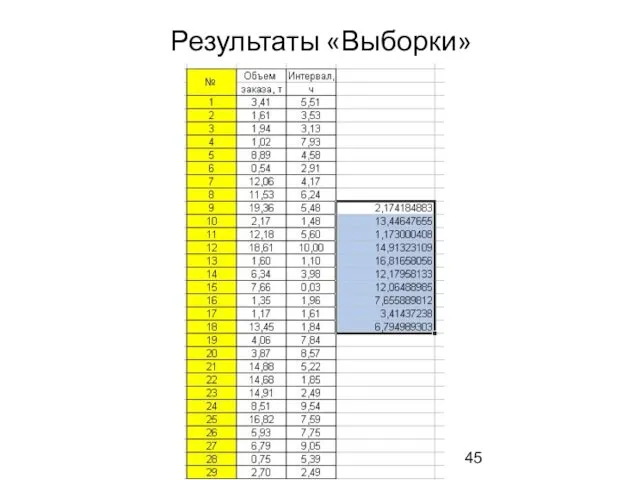
- 45. Результаты «Выборки»
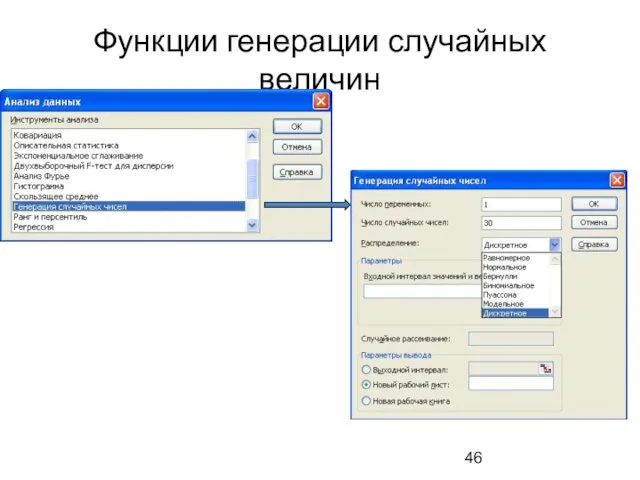
- 46. Функции генерации случайных величин
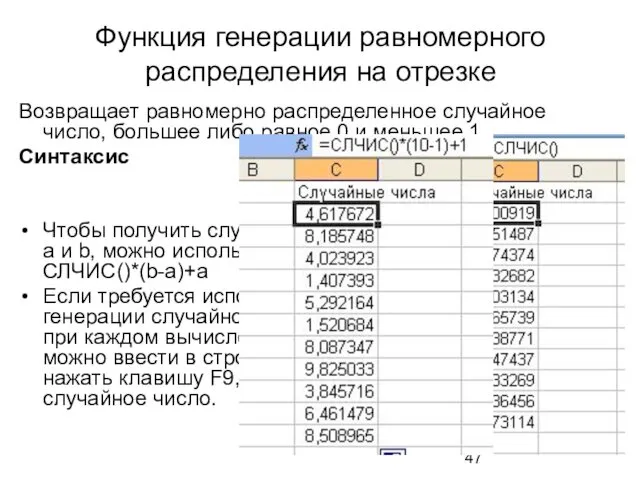
- 47. Функция генерации равномерного распределения на отрезке Возвращает равномерно распределенное случайное число, большее либо равное 0 и
- 48. Генерация случайных чисел по равномерному закону распределения Приведенная реализация случайной величины с интервалом [0, 1] к
- 49. Генерация случайных чисел по нормальному закону распределения Нормально распределенная случайная величина N01 с нулевым математическим ожиданием
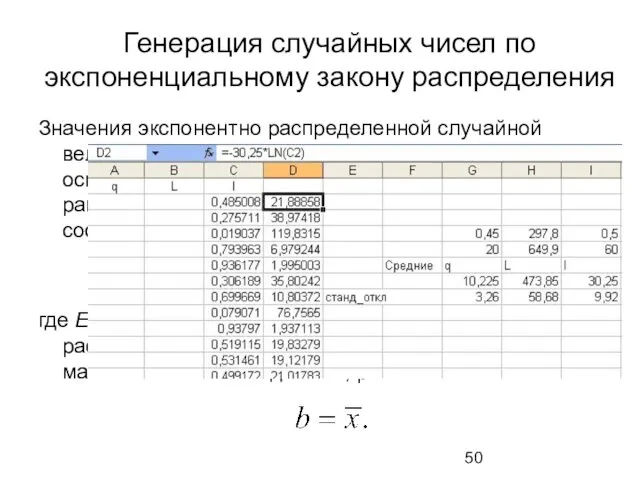
- 50. Генерация случайных чисел по экспоненциальному закону распределения Значения экспонентно распределенной случайной величины с параметром масштаба b
- 51. 3. Прикладной пакет Statistica. ПП STATISTICA – это универсальная интегрированная система, предназначенная для статистического анализа и
- 52. История создания пакета Statistica Система STATISTICA производится фирмой StatSoft Inc. (США), основанной в 1984 г. в
- 54. Решение задач с помощью ПП Statistica (Base) Описательные и внутригрупповые статистики, разведочный анализ данных Корреляции Быстрые
- 55. Описательные статистики и графики Программа вычисляет практически все используемые описательные статистики общего характера: медиану, моду, квартили,
- 57. Скачать презентацию





























 Подготовка к ЕГЭ по математике. Решение задач В12
Подготовка к ЕГЭ по математике. Решение задач В12 Производная функции
Производная функции Подготовка к итоговой аттестации по математике в 9 классе
Подготовка к итоговой аттестации по математике в 9 классе Ehtimalın klassik tərifi
Ehtimalın klassik tərifi Лекция 1.2. Классическое определение вероятности
Лекция 1.2. Классическое определение вероятности Формулы в математике
Формулы в математике Решение задач в два действия. 1 класс
Решение задач в два действия. 1 класс Метод середніх величин
Метод середніх величин Признаки параллельности прямых. Тест. Задачи
Признаки параллельности прямых. Тест. Задачи Решение задач с помощью уравнений
Решение задач с помощью уравнений Выражения со скобками
Выражения со скобками Тест по теме: Объем шара и площадь сферы
Тест по теме: Объем шара и площадь сферы Проектная работа Математическая сказка для 4 класса.
Проектная работа Математическая сказка для 4 класса. Презентация к уроку математики Приметр многоугольника.
Презентация к уроку математики Приметр многоугольника. Отрезок и ломаная. УМК Планета знаний, 1 класс.
Отрезок и ломаная. УМК Планета знаний, 1 класс. урок математики 3 класс Сложение и вычитание величин
урок математики 3 класс Сложение и вычитание величин Теорема Виета. 8 класс
Теорема Виета. 8 класс Параллельность прямой и плоскости. Решение задач
Параллельность прямой и плоскости. Решение задач Устное умножение круглых сотен. 1 часть
Устное умножение круглых сотен. 1 часть Пирамида. Правильная пирамида
Пирамида. Правильная пирамида Дифференциальное и интегральное исчисление
Дифференциальное и интегральное исчисление Электронно-демонстрационная игра
Электронно-демонстрационная игра Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Координатная плоскость
Координатная плоскость Экономико-математические методы и модели в логистике
Экономико-математические методы и модели в логистике Усеченная пирамида
Усеченная пирамида Приемы коррекционного обучения детей с ОВЗ на уроках математики
Приемы коррекционного обучения детей с ОВЗ на уроках математики Показательная функция, ее свойства и график
Показательная функция, ее свойства и график