Содержание
- 2. Утв. (об аналитичности композиции АФ). Если w = f(z)∈A(D(z)), а в области ее значений E(w) определена
- 3. Утв. (об аналитичности обратной функции). Утв. (о бесконечной дифференцируемости АФ). Функция f(z), аналитическая в области D
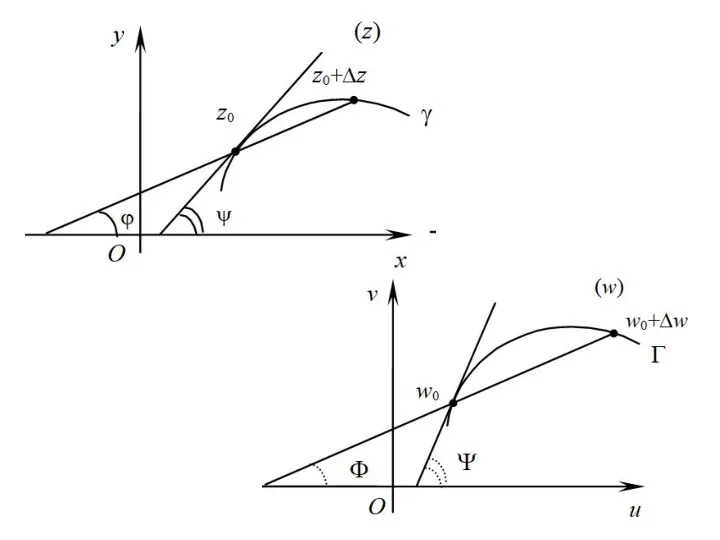
- 4. Геометрический смысл производной ФКП Пусть w = f(z) – аналитическая в точке z0 .
- 6. - коэффициент локального растяжения (k>1) или сжатия (k − это угол, на который нужно повернуть касательную
- 7. Понятие конформного отображения Опр. Отображение окрестности точки z0 на окрестность точки w0, осуществляемое функцией w =
- 8. Т. (критерий конформности). Для того чтобы отображение w = f(z) было конформным в области D, необходимо
- 9. Лекция 5 Интегрирование ФКП
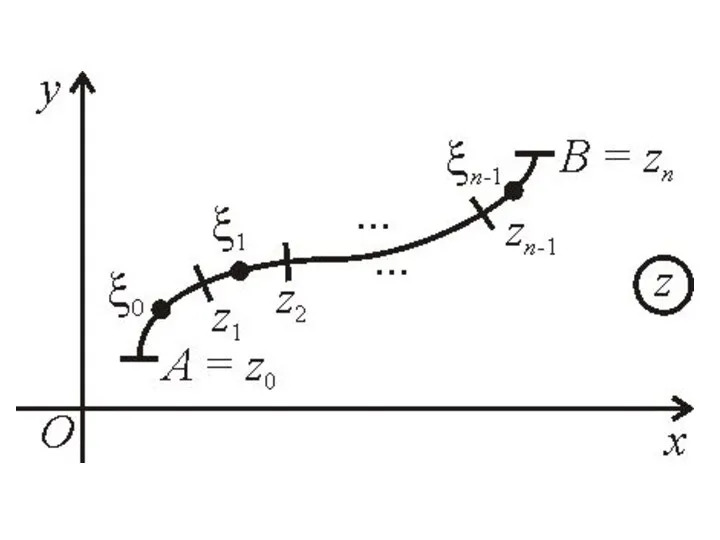
- 10. Пусть на комплексной плоскости задана кривая AB – ориентированная, незамкнутая, кусочно-гладкая, без самопересечений: Разобьем AB произвольным
- 12. Пусть на дуге AB определена ФКП f(z). Найдем ее значения в точках: и составим интегральную сумму:
- 13. не зависящий от способа разбиения дуги AB и выбора точек , то этот предел называют интегралом
- 14. если то если то
- 15. Свойства интеграла от ФКП
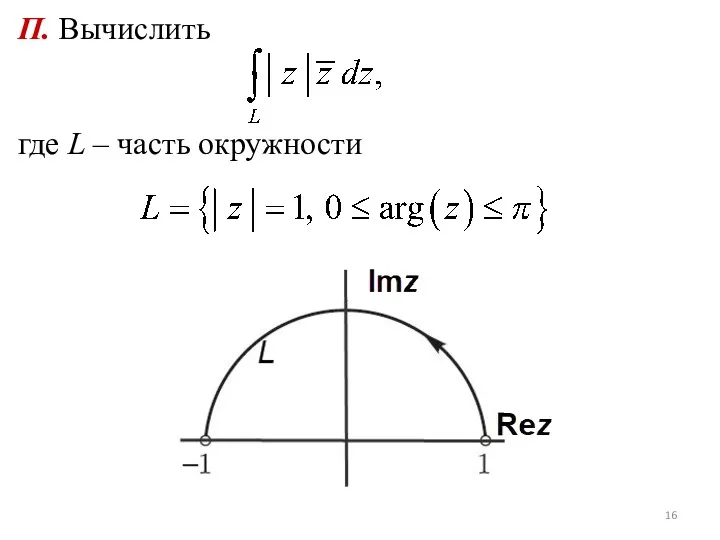
- 16. П. Вычислить где L – часть окружности
- 17. Параметризация:
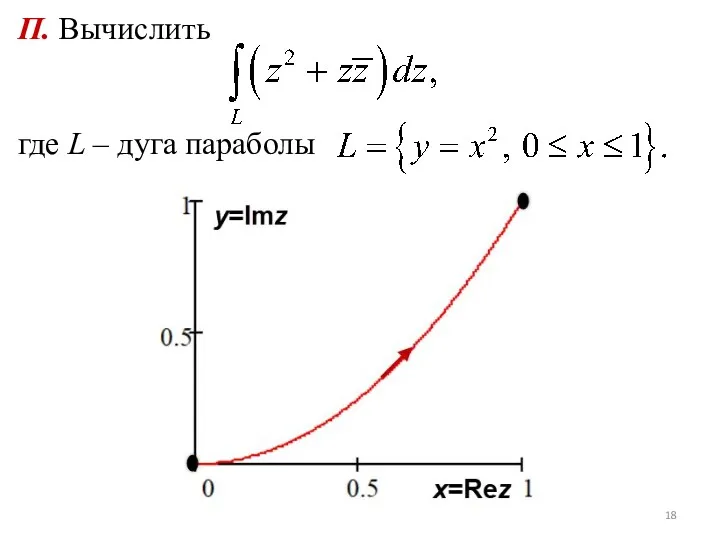
- 18. П. Вычислить где L – дуга параболы
- 19. Выделим действительную и мнимую части подынтегральной функции:
- 21. Скачать презентацию










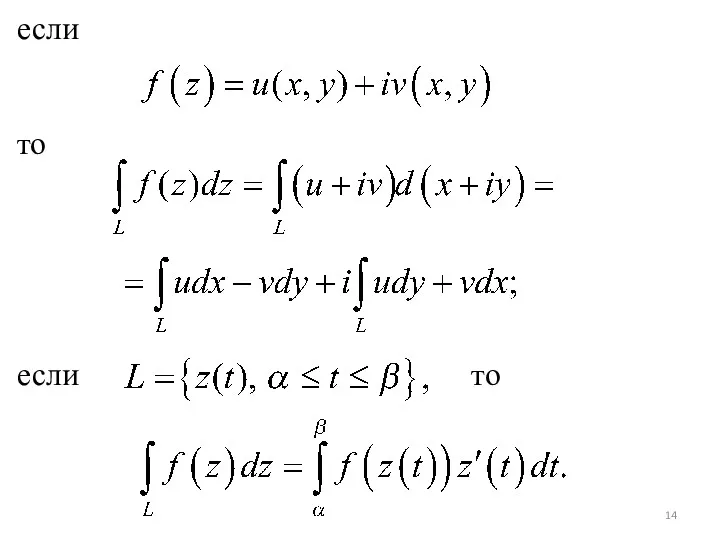

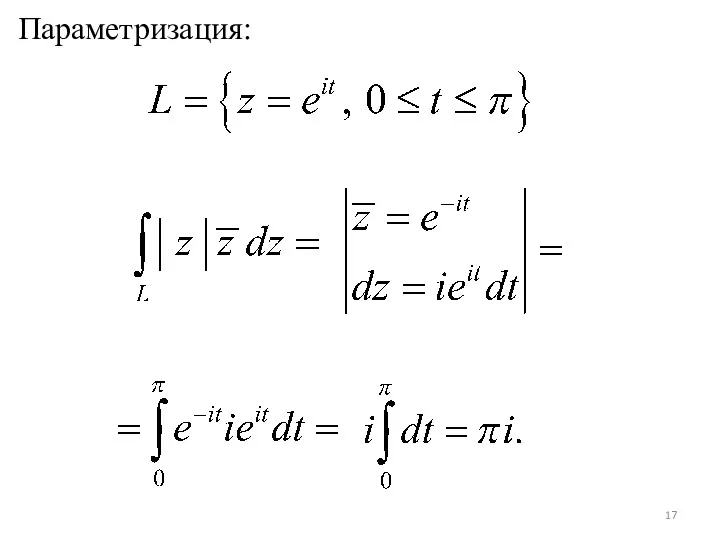

 Исследование функций и построение графиков. Возрастание и убывание функции одной переменной. Определение. (Семинар 12)
Исследование функций и построение графиков. Возрастание и убывание функции одной переменной. Определение. (Семинар 12) Неопределенный интеграл
Неопределенный интеграл Масса
Масса Последовательность комплексных чисел
Последовательность комплексных чисел Диференціальне числення. Визначення функції ( лекція 1.1)
Диференціальне числення. Визначення функції ( лекція 1.1)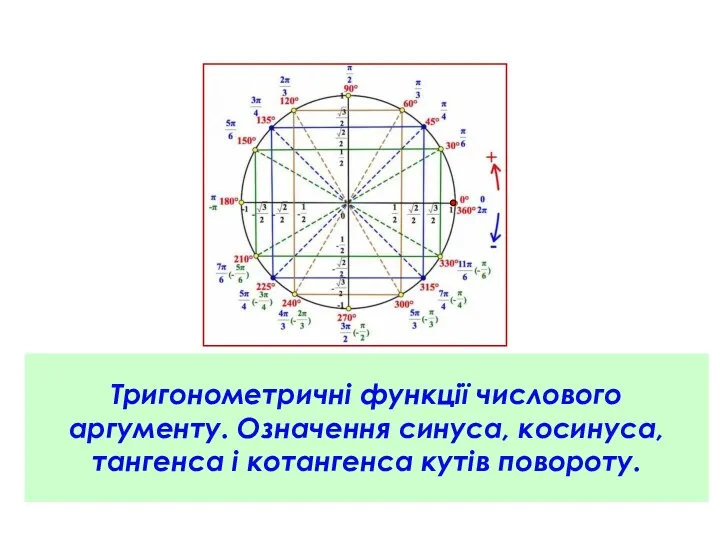 Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2
Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2 Презентация Кубик Рубика 1 класс
Презентация Кубик Рубика 1 класс Зеленая аптека Кузбасса. Проценты
Зеленая аптека Кузбасса. Проценты Второй и третий признаки равенства треугольников. Урок 1
Второй и третий признаки равенства треугольников. Урок 1 Колебания напряжения в бытовых электрических сетях
Колебания напряжения в бытовых электрических сетях Математические ребусы
Математические ребусы Математика. 1 класс. Урок 82. Величины. Решение задач - Презентация
Математика. 1 класс. Урок 82. Величины. Решение задач - Презентация Метапредметные проекты
Метапредметные проекты Школа 2100. 1 класс. Счет в пределах 10. Ломскова Л.В. Диск
Школа 2100. 1 класс. Счет в пределах 10. Ломскова Л.В. Диск Математическое соревнование: Космическое путешествие (7, 9 классы)
Математическое соревнование: Космическое путешествие (7, 9 классы) Угол. Измерение углов
Угол. Измерение углов Столбчатые и линейные диаграммы
Столбчатые и линейные диаграммы Статистические методы анализа данных параметров транспортного процесса
Статистические методы анализа данных параметров транспортного процесса Окружность, круг и их элементы
Окружность, круг и их элементы Презентация Сказка - лучшее учение
Презентация Сказка - лучшее учение Осевая и цетральная симметрия
Осевая и цетральная симметрия Натуральные числа
Натуральные числа Табличные случаи сложения и вычитания в пределах 10
Табличные случаи сложения и вычитания в пределах 10 Внеклассное мероприятие Аукцион математических задач
Внеклассное мероприятие Аукцион математических задач Презентация по математике по теме Задачи на движение4 класс
Презентация по математике по теме Задачи на движение4 класс Итоговый тест по математике №2
Итоговый тест по математике №2 Векторная алгебра. Векторы на плоскости и в пространстве
Векторная алгебра. Векторы на плоскости и в пространстве Пересечение тел проецирующей плоскостью
Пересечение тел проецирующей плоскостью