Содержание
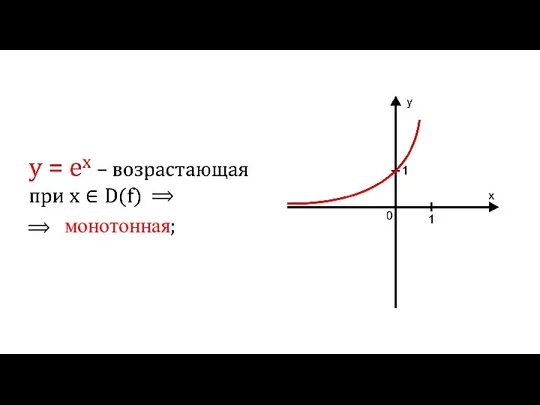
- 2. ⟹ ⟹ монотонная;
- 3. Если функция у = f(х), х ∈ Х принимает любое свое значение только в одной точке
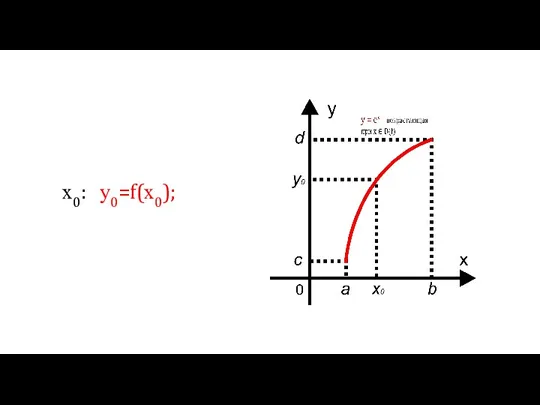
- 4. х0: у0=f(х0);
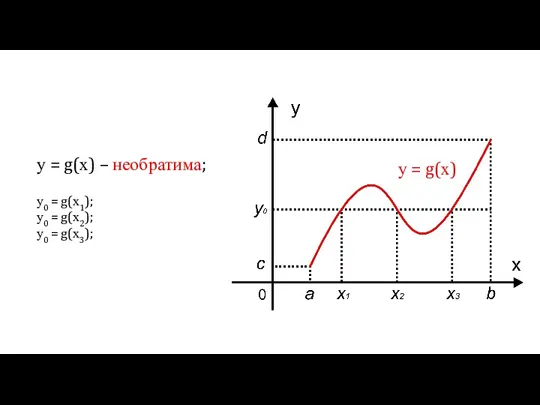
- 5. у = g(х) у = g(х) – необратима; у0 = g(х1); у0 = g(х2); у0 =
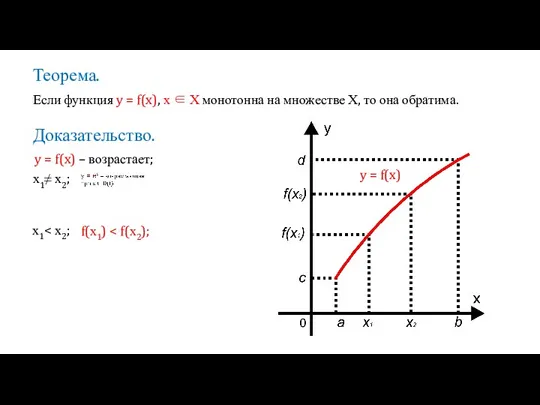
- 6. Теорема. Если функция y = f(x), х ∈ Х монотонна на множестве Х, то она обратима.
- 7. y = f(x) – обратимая функция; x = f –1(y) – обратная функция; определена на множестве
- 8. 1. Область определения функции у = f(х): Х является областью значений функции x = f -1(y).
- 9. у = f(х) – возрастающая функция; у1 =f(х1) ; у2 = f(х2) ; х1 х1 ≥
- 10. Пример 1. Показать, что для функции y = 3x – 2 существует обратная функция, и найти
- 11. Решение. y = x²— квадратичная функция; D(у) = R; возрастает на [0;∞); убывает на (-∞;0]; на
- 12. Пример 3. Найти обратную функцию к функции у = х3. Решение. D(у) = R;
- 13. монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием. Замечание:
- 15. Скачать презентацию








 Прямоугольные треугольники и их свойства
Прямоугольные треугольники и их свойства Виды алгоритмических структур. Линейный алгоритм. Свойства алгоритма
Виды алгоритмических структур. Линейный алгоритм. Свойства алгоритма Презентация к уроку математике во 2 классе Сложение одинаковых слагаемых
Презентация к уроку математике во 2 классе Сложение одинаковых слагаемых Стандартный вид числа
Стандартный вид числа Точки перегиба функции, выпуклость графика функции
Точки перегиба функции, выпуклость графика функции The Taylor Formula
The Taylor Formula Столбчатые и круговые диаграммы
Столбчатые и круговые диаграммы Новый приём вычислений
Новый приём вычислений Прямые. Взаимное расположение прямых в пространстве. Признак скрещивающихся прямых
Прямые. Взаимное расположение прямых в пространстве. Признак скрещивающихся прямых Математические диктанты. Обыкновенные дроби
Математические диктанты. Обыкновенные дроби Случаи сложения вида +4
Случаи сложения вида +4 Презентация и конспект к уроку во 2 классе по теме: Длина ломанной. Периметр многоугольника А.Милн Винни – Пух и его друзья составлен по программе Школа 2000. автор Л.Г.Петресон. Урок предусматривает закрепления и уточнение
Презентация и конспект к уроку во 2 классе по теме: Длина ломанной. Периметр многоугольника А.Милн Винни – Пух и его друзья составлен по программе Школа 2000. автор Л.Г.Петресон. Урок предусматривает закрепления и уточнение Урок математики по теме Перестановка слагаемых 1 класс
Урок математики по теме Перестановка слагаемых 1 класс Презентация по теме Доли Математика 3 класс М.И. Моро
Презентация по теме Доли Математика 3 класс М.И. Моро Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Відстані в просторі
Відстані в просторі Обратные функции. 10 класс
Обратные функции. 10 класс Понятие движения
Понятие движения Тела вращения. Вычисление площади поверхности
Тела вращения. Вычисление площади поверхности Квадратичная функция, ее график и свойства
Квадратичная функция, ее график и свойства Вычитание чисел в пределах 20 с переходом через разряд
Вычитание чисел в пределах 20 с переходом через разряд Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Презентации к урокам Диск
Презентации к урокам Диск Возможности и использование системы компьютерной математики Scilab. Тема 3
Возможности и использование системы компьютерной математики Scilab. Тема 3 Математик - царица всех наук. Викторина
Математик - царица всех наук. Викторина Ықтималдықтың элементтері, математикалық статистика элементтері. Ыктималдықтарды қосу және көбейту
Ықтималдықтың элементтері, математикалық статистика элементтері. Ыктималдықтарды қосу және көбейту Метрология. Результаты измерений и их обработка
Метрология. Результаты измерений и их обработка Формулы сокращённого умножения. 7 класс
Формулы сокращённого умножения. 7 класс