Теорема Пифагора презентация

Проверка домашнего задания
1). Сформулировать и доказать теорему Пифагора.
2). Привести еще одно доказательство теоремы Пифагора путем построения квадратов на сторонах треугольника.

Доказательство теоремы Пифагора путем построения квадратов на сторонах треугольника.
В Древней Индии, доказывая теорему, часто приводили только рисунок и сопровождали его лишь одним словом «Смотри».
Сравнить рисунки нетрудно, а в них вся суть доказательства.

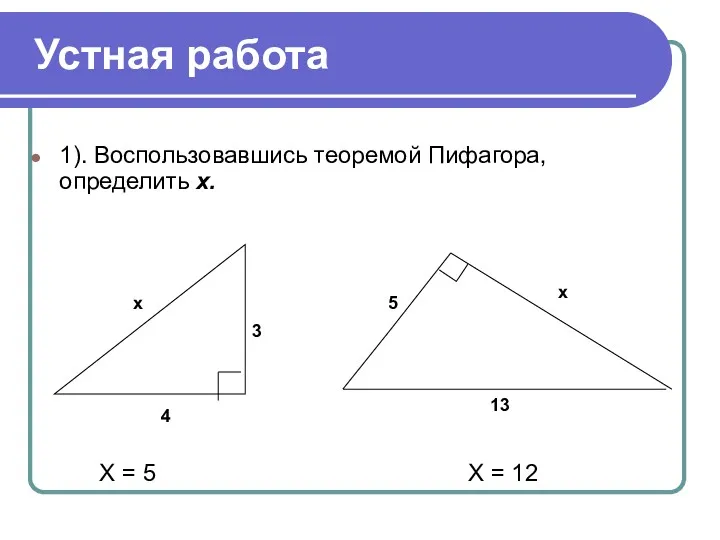
Устная работа
1). Воспользовавшись теоремой Пифагора, определить х.
4
3
х
13
5
х
Х = 5
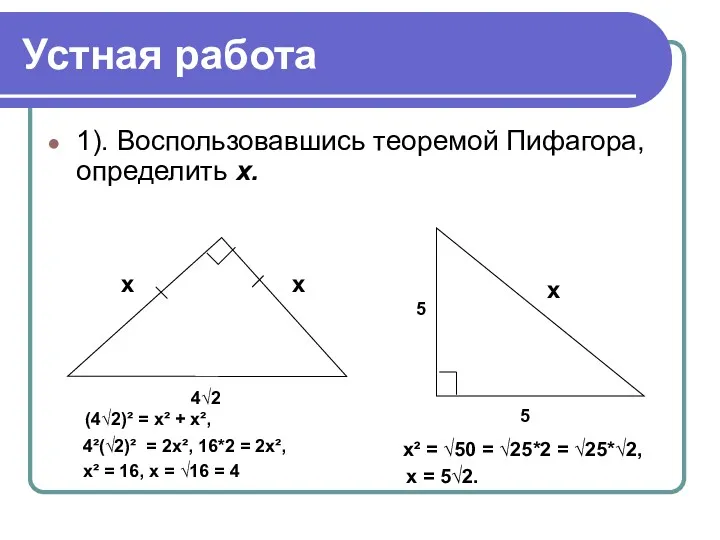
Х = 12

Устная работа
1). Воспользовавшись теоремой Пифагора, определить х.
х
х
4√2
5
5
х
(4√2)² = х² + х²,
4²(√2)² = 2х², 16*2 = 2х²,
х² = 16, х = √16 = 4
х² = √50 = √25*2 = √25*√2,
х = 5√2.

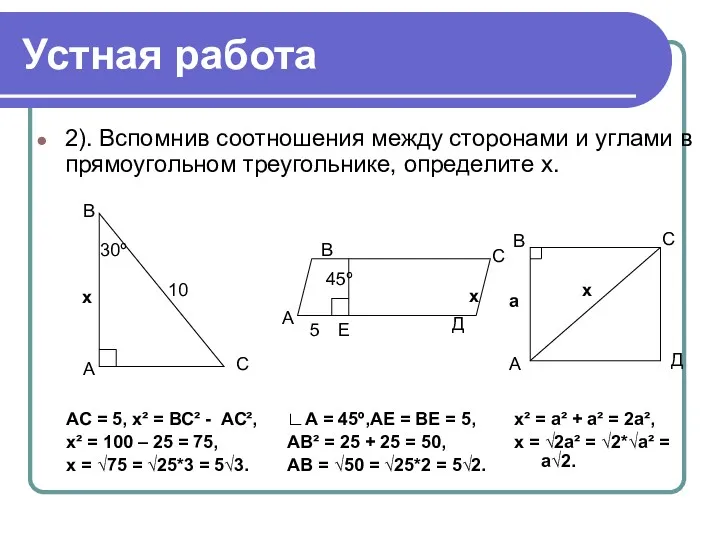
Устная работа
2). Вспомнив соотношения между сторонами и углами в прямоугольном треугольнике, определите х.
А
В
10
х
В
С
Д
А
Е 45º
5
х
А
В
С
Д
а
х
АС = 5, х² = ВС² - АС²,
х² = 100 – 25 = 75,
х = √75 = √25*3 = 5√3.
∟А = 45º,АЕ = ВЕ = 5,
АВ² = 25 + 25 = 50,
АВ = √50 = √25*2 = 5√2.
х² = а² + а² = 2а²,
х = √2а² = √2*√а² = а√2.
С
30º

В тетрадях № 494 (из учебника)

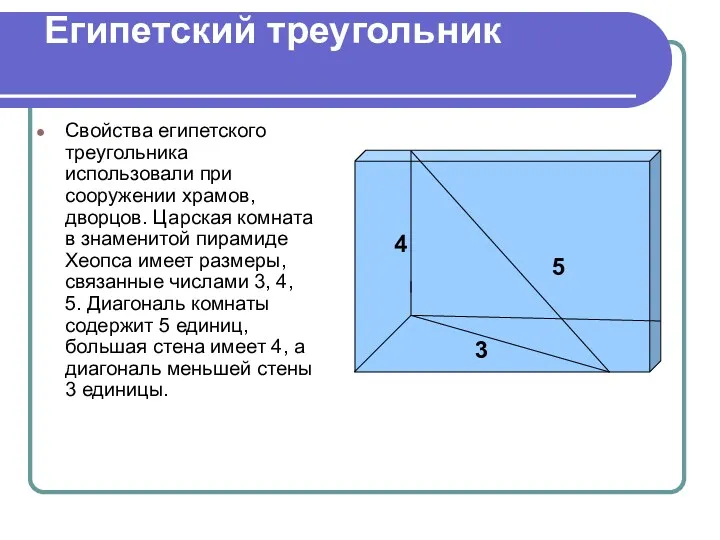
Изучение новой темы
Египетский треугольник.
Треугольник со сторонами 3, 4, 5 назвали египетским. Название такое получил потому, что еще в Древнем Египте для построения прямых углов на местности использовали именно этот способ.

Свойства египетского треугольника использовали при сооружении храмов, дворцов. Царская комната в знаменитой пирамиде Хеопса имеет размеры, связанные числами 3, 4, 5. Диагональ комнаты содержит 5 единиц, большая стена имеет 4, а диагональ меньшей стены 3 единицы.
5
4
3
Египетский треугольник

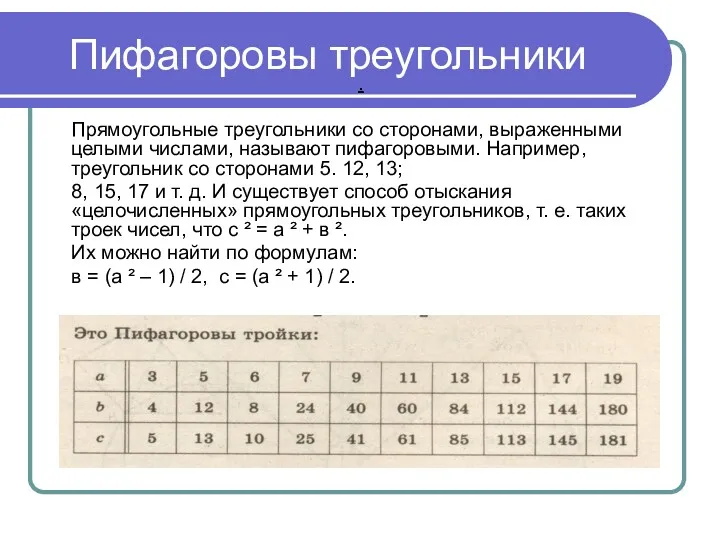
Пифагоровы треугольники
.
Прямоугольные треугольники со сторонами, выраженными целыми числами, называют пифагоровыми. Например, треугольник со сторонами 5. 12, 13;
8, 15, 17 и т. д. И существует способ отыскания «целочисленных» прямоугольных треугольников, т. е. таких троек чисел, что с ² = а ² + в ².
Их можно найти по формулам:
в = (а ² – 1) / 2, с = (а ² + 1) / 2.

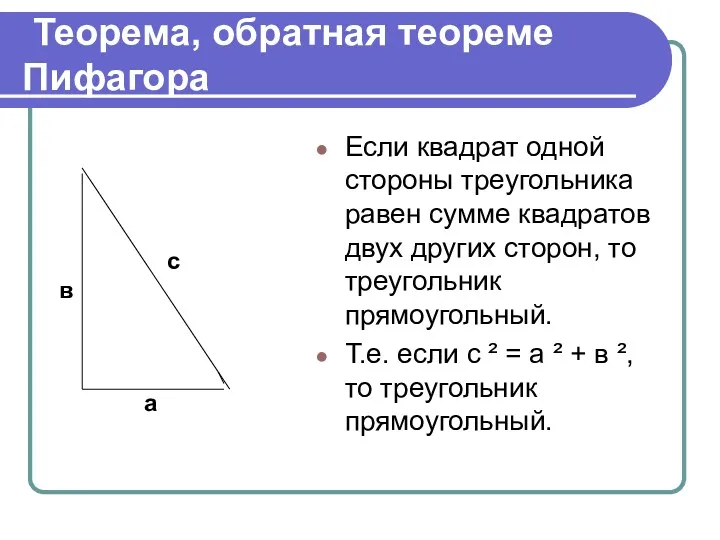
Теорема, обратная теореме Пифагора
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Т.е. если с ² = а ² + в ², то треугольник прямоугольный.
с
а
в

Самостоятельная работа
Дается на карточках (4 варианта). Второе задание дополнительное, предназначенное для сильных учащихся. Можно использовать микрокалькуляторы.