Содержание
- 2. А. Основная литература Волченская Т.В., Князьков В.С. Компьютерная математика: ч.2. Теория графов: Учеб. пособие. - 2007.
- 3. Б. Дополнительная литература Белоусов А. И., Ткачев С. Б. Дискретная математика. – М.: Изд-во МГТУ им
- 4. 1. Введение и области применения теории графов 2. Способы представления графов 3. Основные операции на графах
- 5. Введение В последние годы особую важность приобрели те разделы математики, которые имеют отношение к развитию цифровых
- 6. Комбинаторные вычисления находят широкое применение в различных областях : Производство РЭА и ВТ оптимальное размещение элементов
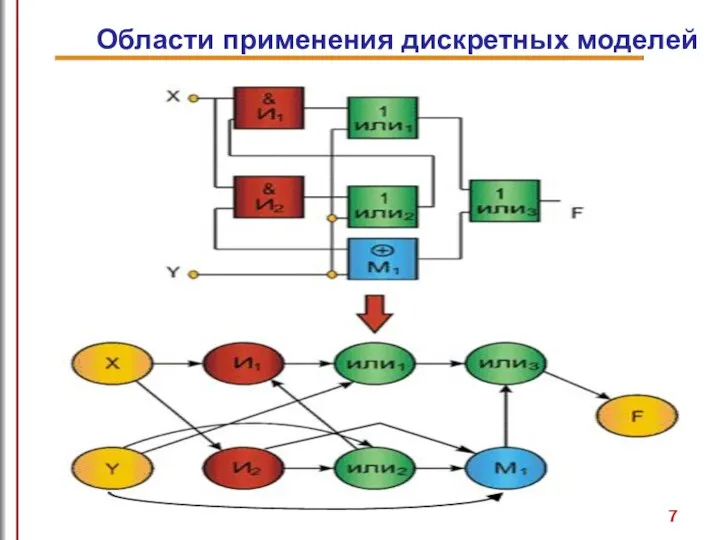
- 7. Области применения дискретных моделей
- 8. 2. Строительство Как построить транспортную сеть в регионе, чтобы минимизировать затраты на строительство и оптимизировать транспортные
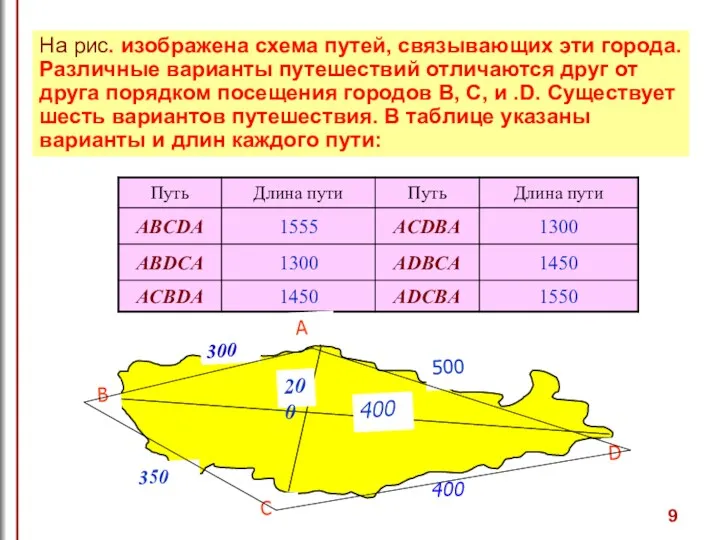
- 9. На рис. изображена схема путей, связывающих эти города. Различные варианты путешествий отличаются друг от друга порядком
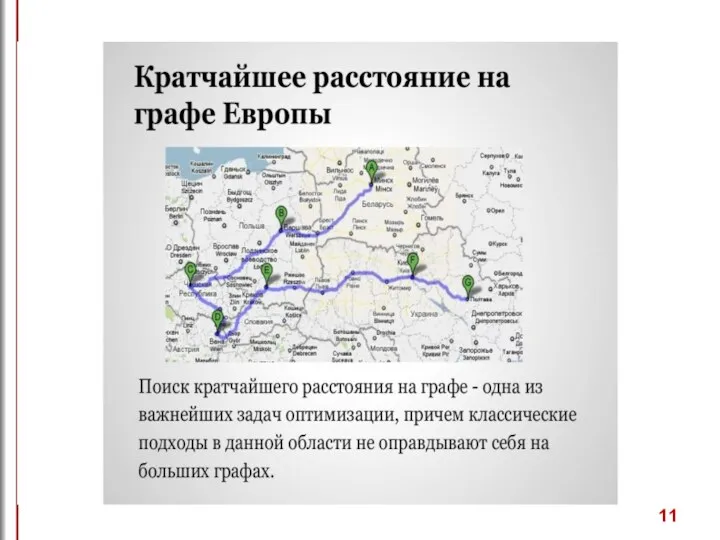
- 12. Области применения дискретных моделей
- 13. Области применения дискретных моделей при исследовании так называемой проблемы оптимизации, возникающей при конструировании больших систем как
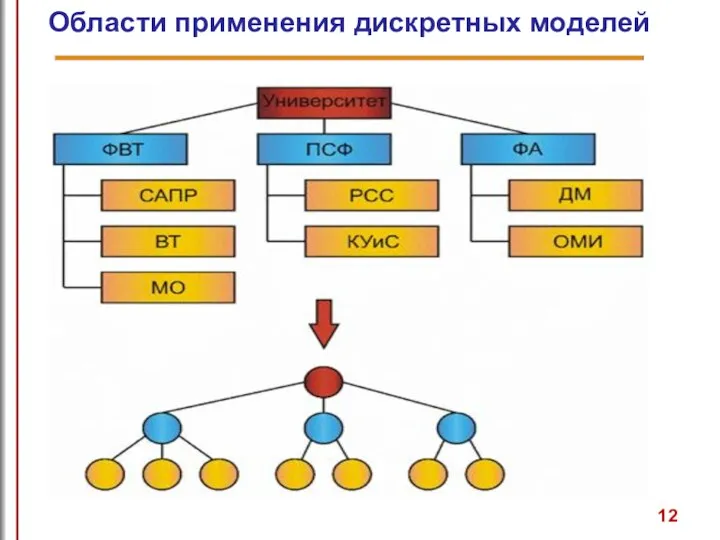
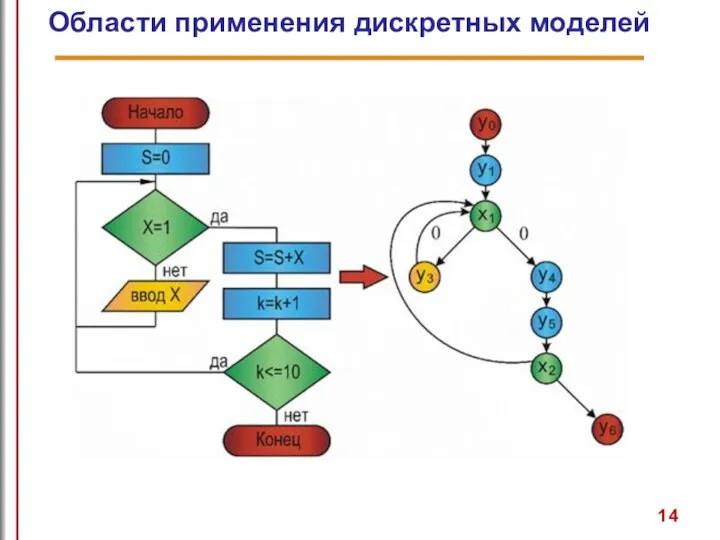
- 14. Области применения дискретных моделей
- 15. Графы и способы их представления
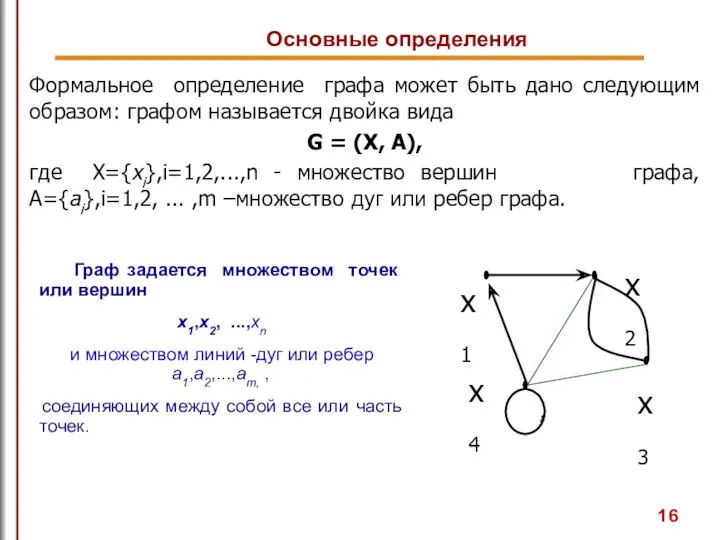
- 16. Основные определения Граф задается множеством точек или вершин х1,х2, ...,хn и множеством линий -дуг или ребер
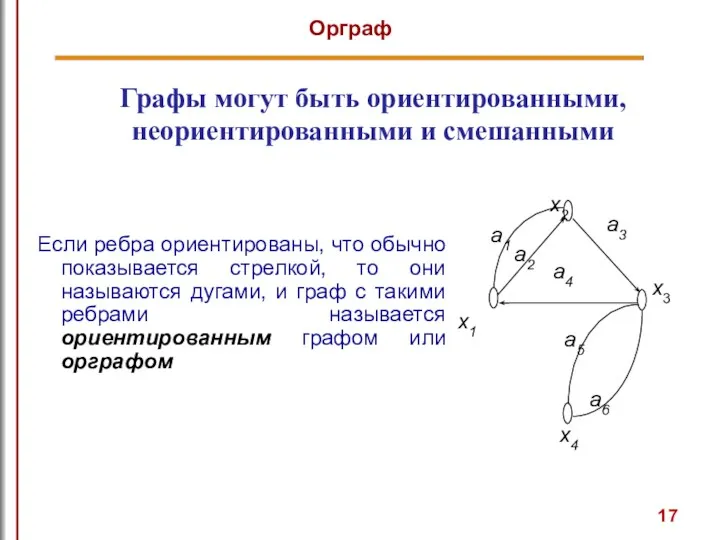
- 17. Графы могут быть ориентированными, неориентированными и смешанными Если ребра ориентированы, что обычно показывается стрелкой, то они
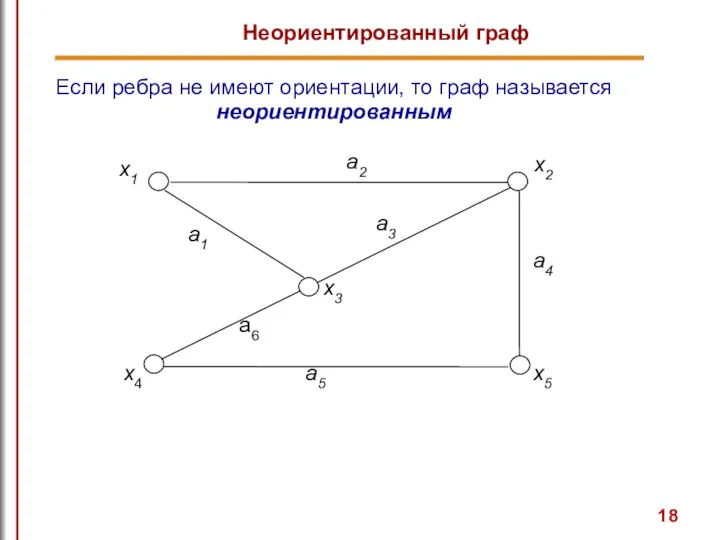
- 18. Если ребра не имеют ориентации, то граф называется неориентированным Неориентированный граф
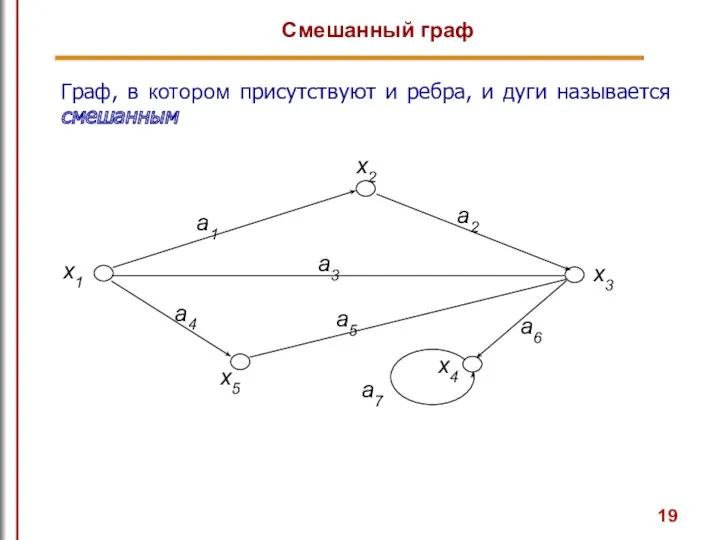
- 19. Граф, в котором присутствуют и ребра, и дуги называется смешанным Смешанный граф
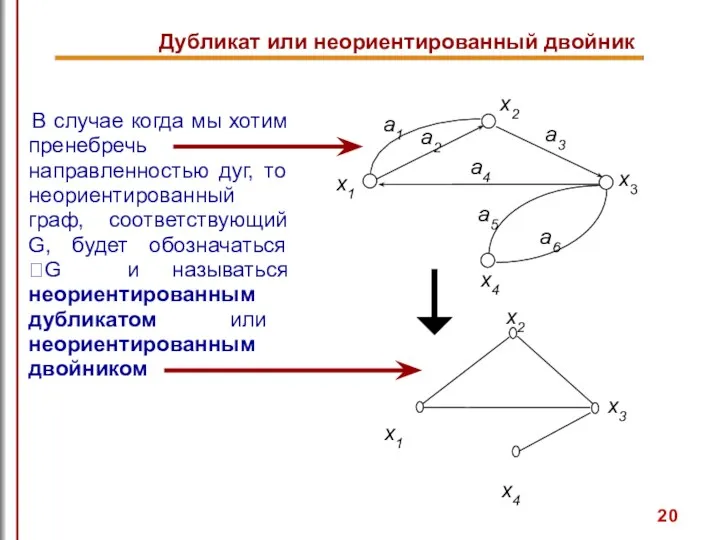
- 20. Дубликат или неориентированный двойник В случае когда мы хотим пренебречь направленностью дуг, то неориентированный граф, соответствующий
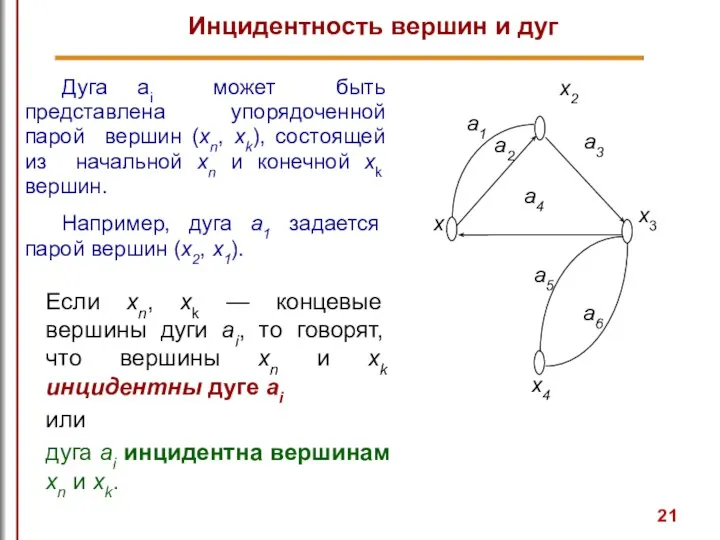
- 21. Инцидентность вершин и дуг Дуга ai может быть представлена упорядоченной парой вершин (xn, xk), состоящей из
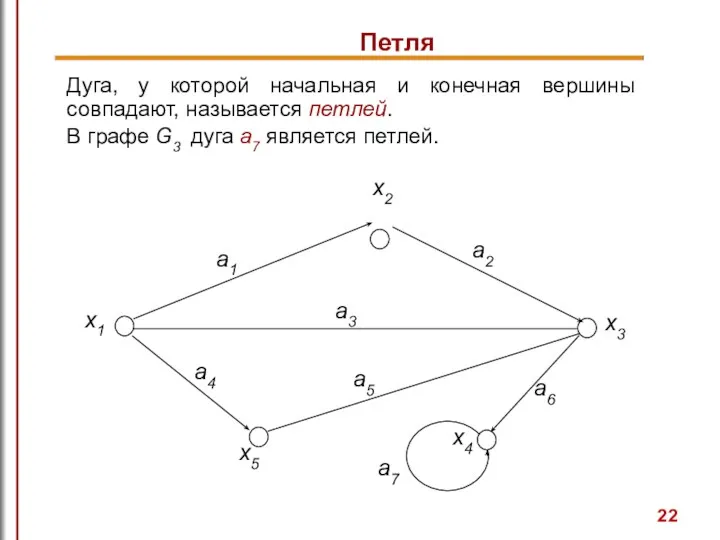
- 22. Петля Дуга, у которой начальная и конечная вершины совпадают, называется петлей. В графе G3 дуга а7
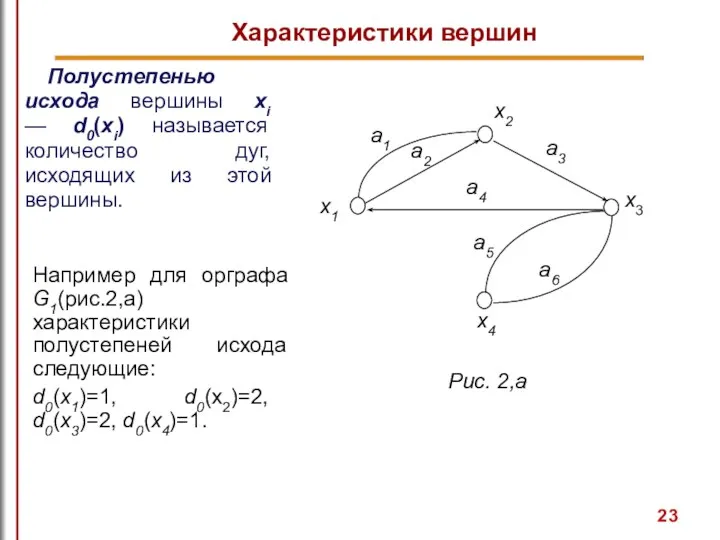
- 23. Характеристики вершин Полустепенью исхода вершины xi — d0(xi) называется количество дуг, исходящих из этой вершины. Например
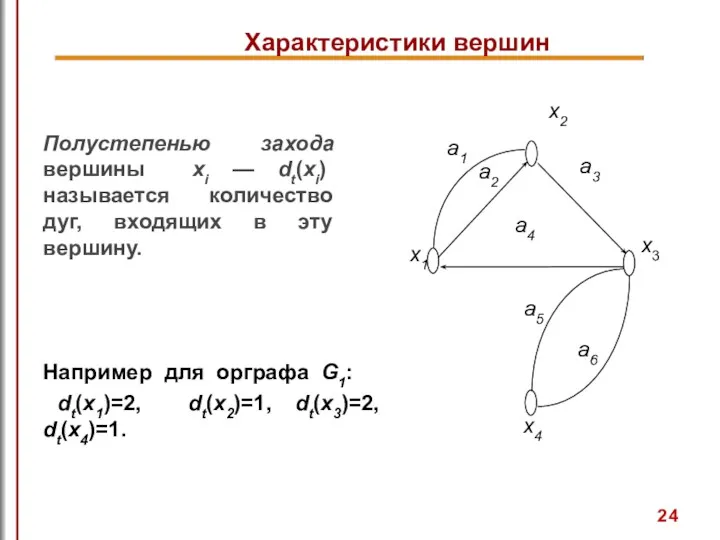
- 24. Характеристики вершин Полустепенью захода вершины xi — dt(xi) называется количество дуг, входящих в эту вершину. Например
- 25. Очевидно, что сумма полустепеней исхода всех вершин графа, а также сумма полустепеней захода всех вершин графа
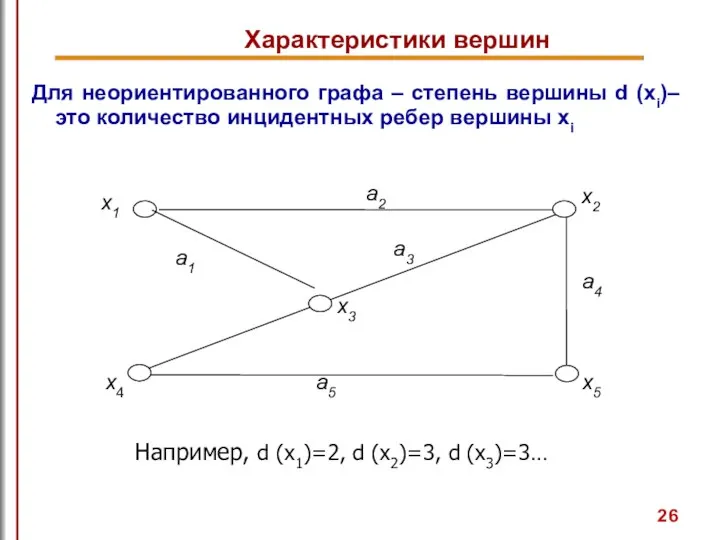
- 26. Для неориентированного графа – степень вершины d (xi)– это количество инцидентных ребер вершины xi Характеристики вершин
- 27. Способы описания графов Теоретико-множественное описание Описание отображениями Графическое Матричное
- 28. Теоретико-множественное представление графов Граф описывается явным перечислением элементов множеств вершин и дуг. Примеры описания приведены для
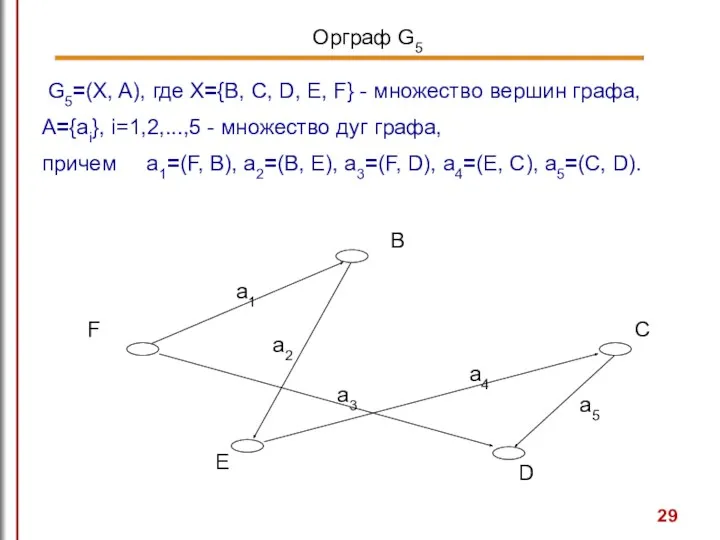
- 29. G5=(X, A), где X={B, C, D, E, F} - множество вершин графа, A={ai}, i=1,2,...,5 - множество
- 30. Задание графов отображениями Описание графов состоит в задании множества вершин Х и соответствий Г или отображений
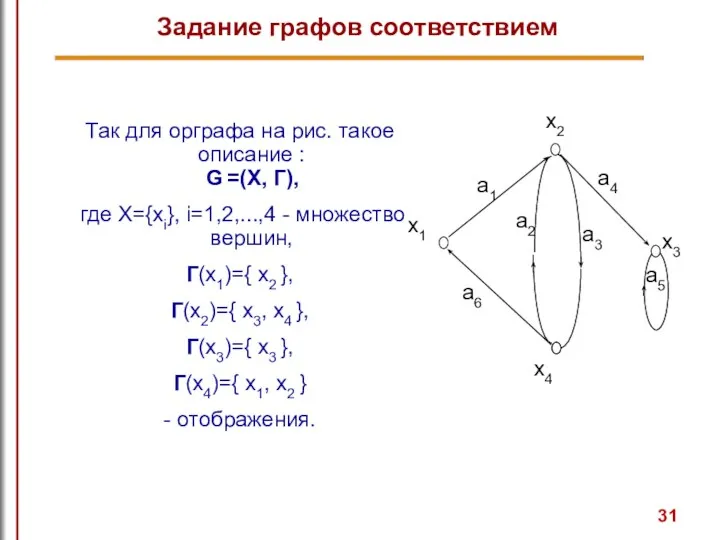
- 31. Так для орграфа на рис. такое описание : G =(X, Г), где X={xi}, i=1,2,...,4 - множество
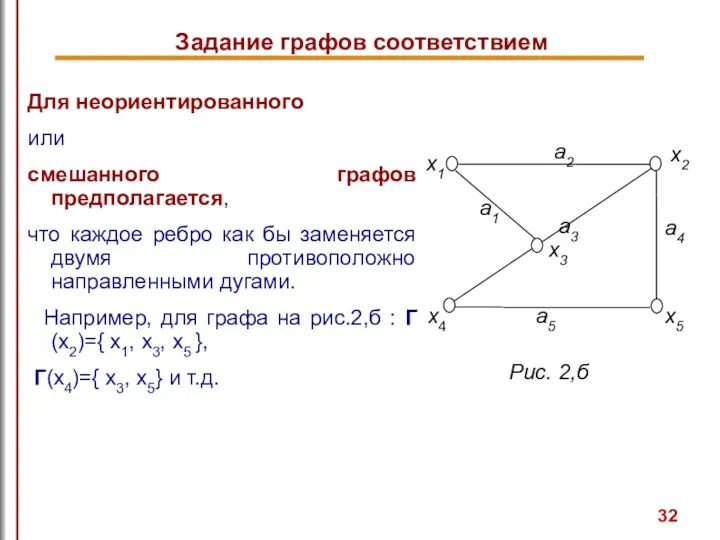
- 32. Задание графов соответствием Для неориентированного или смешанного графов предполагается, что каждое ребро как бы заменяется двумя
- 33. Матричное представление графов Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций.
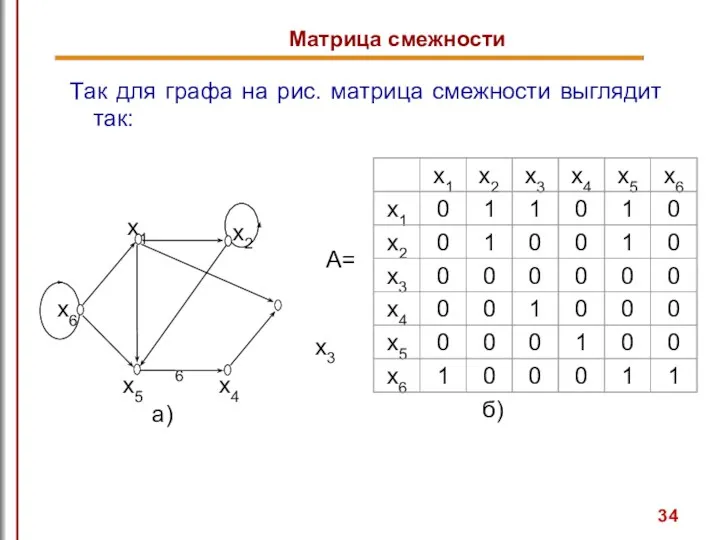
- 34. Матрица смежности Так для графа на рис. матрица смежности выглядит так: x3
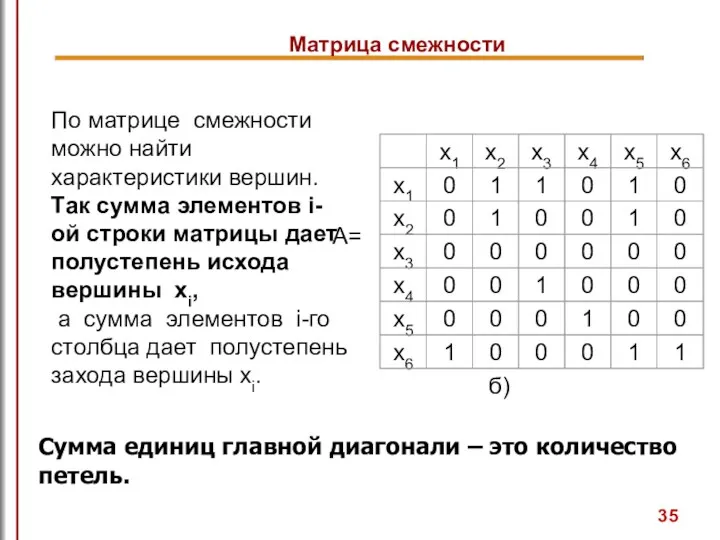
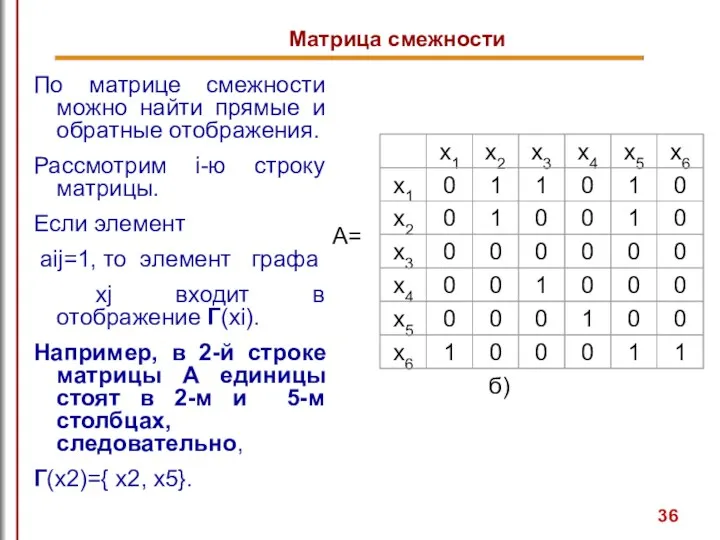
- 35. По матрице смежности можно найти характеристики вершин. Так сумма элементов i-ой строки матрицы дает полустепень исхода
- 36. Матрица смежности По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i-ю строку матрицы. Если
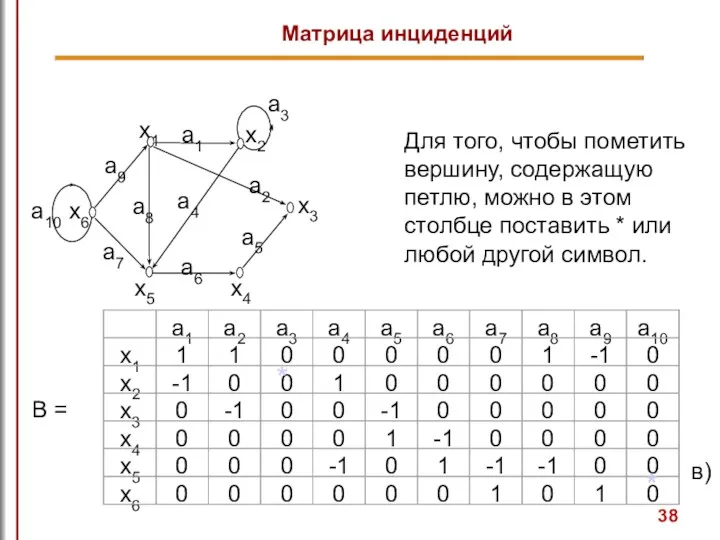
- 37. Матрица инциденций Матрица инциденций - это прямоугольная матрица размером n ×m, где n- количество вершин графа,
- 38. * Для того, чтобы пометить вершину, содержащую петлю, можно в этом столбце поставить * или любой
- 39. По матрице инциденций можно найти характеристики графа: Число 1 в i-ой строке– это d0(xi) * *
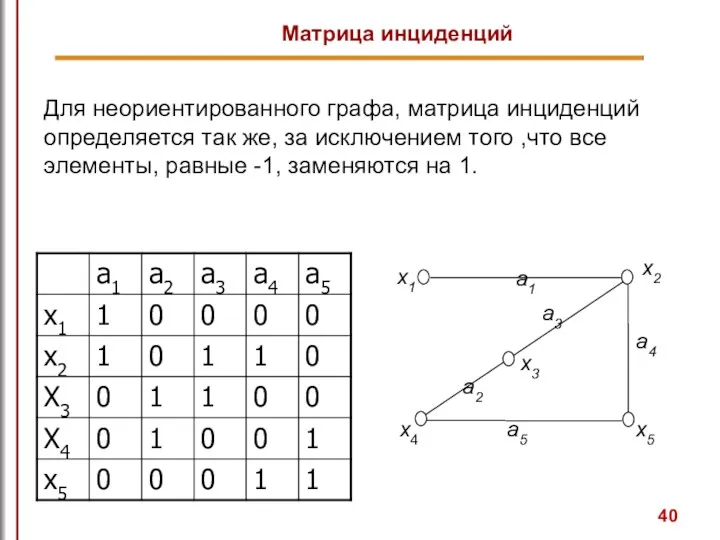
- 40. Для неориентированного графа, матрица инциденций определяется так же, за исключением того ,что все элементы, равные -1,
- 41. Операции над графами Рассмотрим семь операций над графами, три из которых являются бинарными, включающими два графа,
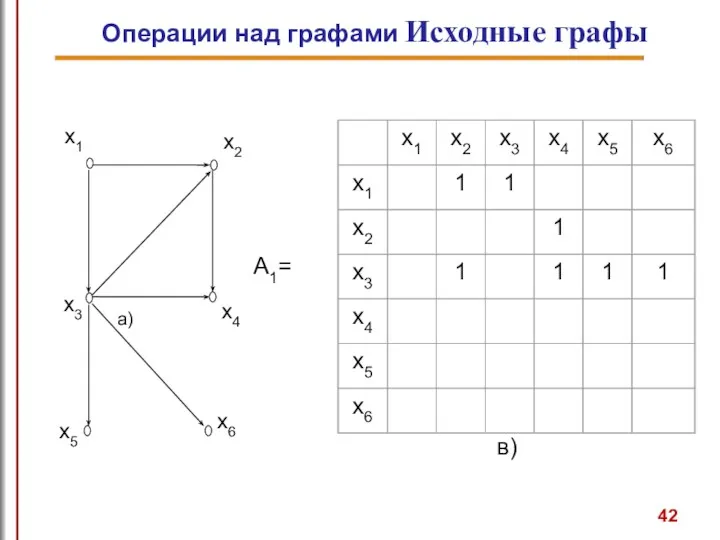
- 42. Операции над графами Исходные графы
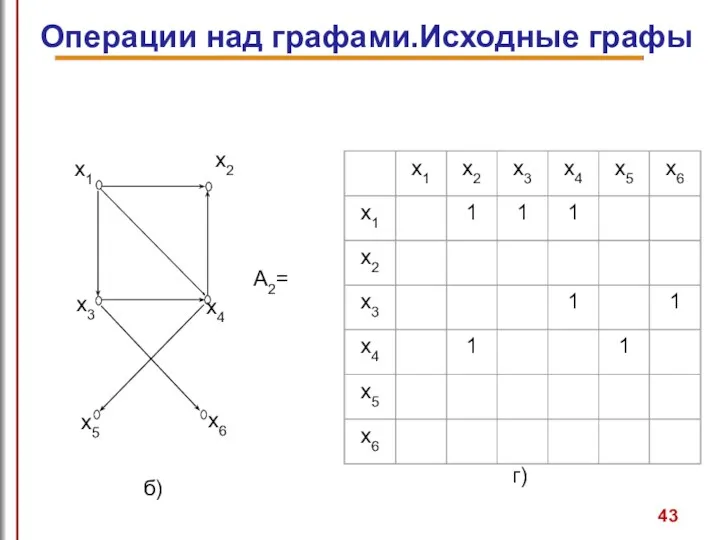
- 43. Операции над графами.Исходные графы б)
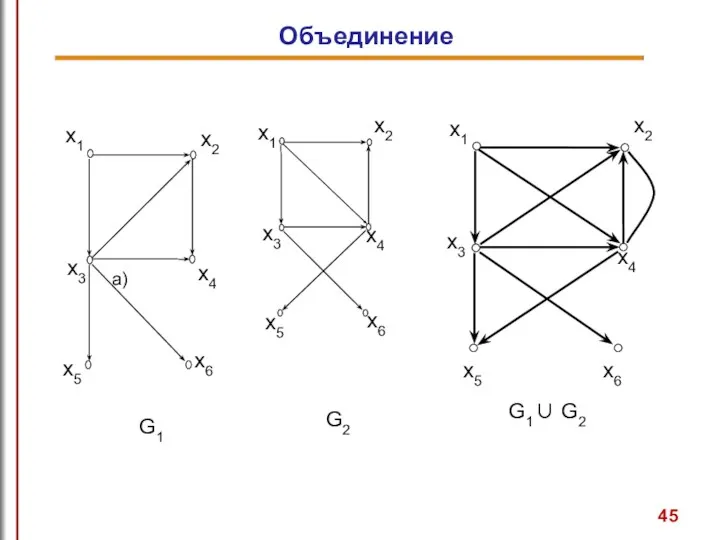
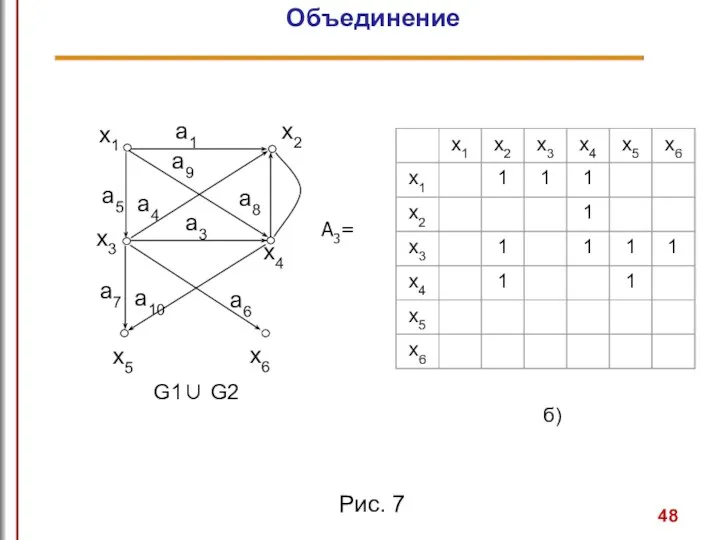
- 44. Объединение графов G1 и G2, обозначаемое как G1 ∪ G2, представляет такой граф G3=(X1 ∪ X2,
- 45. Объединение x3
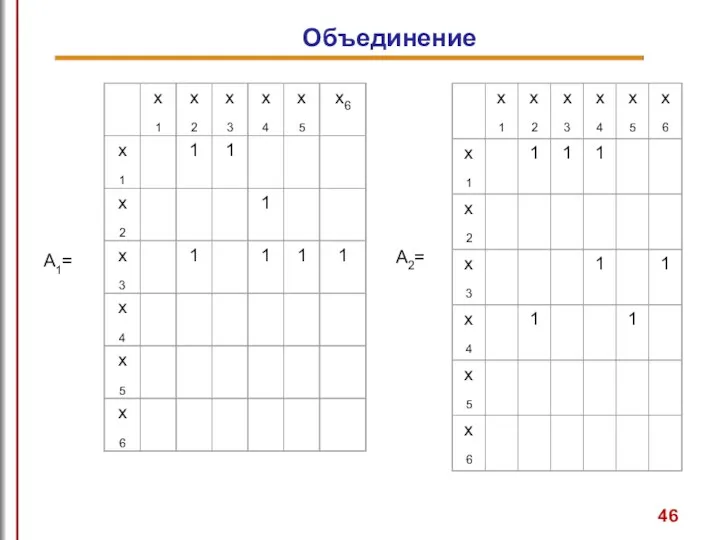
- 46. Объединение
- 47. Объединение
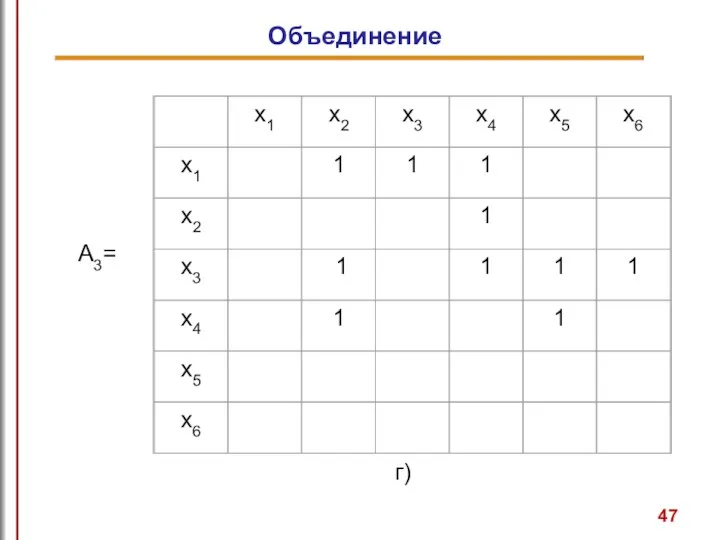
- 48. Рис. 7 Объединение
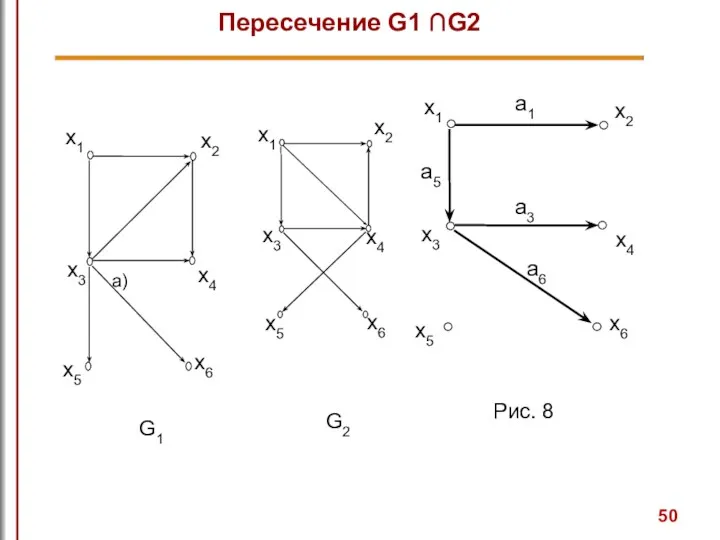
- 49. Пересечение графов G1 и G2, обозначаемое как G1 ∩G2, представляет собой граф G4=(X1 ∩X2, A1 ∩A2).
- 50. Пересечение G1 ∩G2
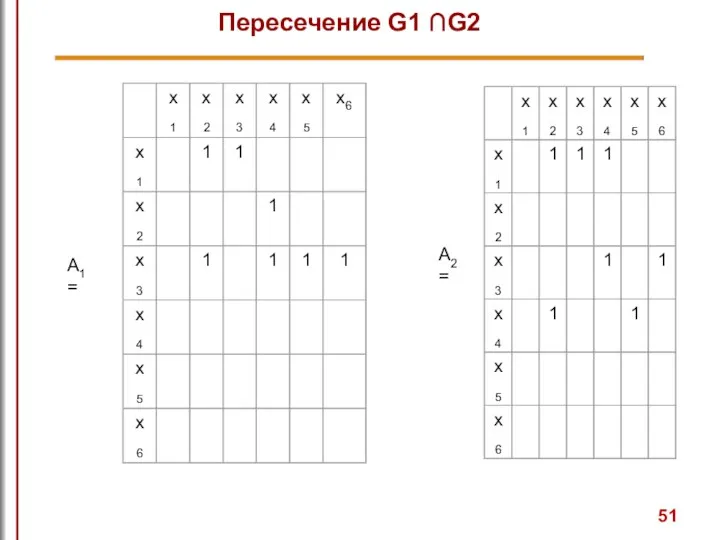
- 51. Пересечение G1 ∩G2
- 52. Пересечение G1 ∩G2
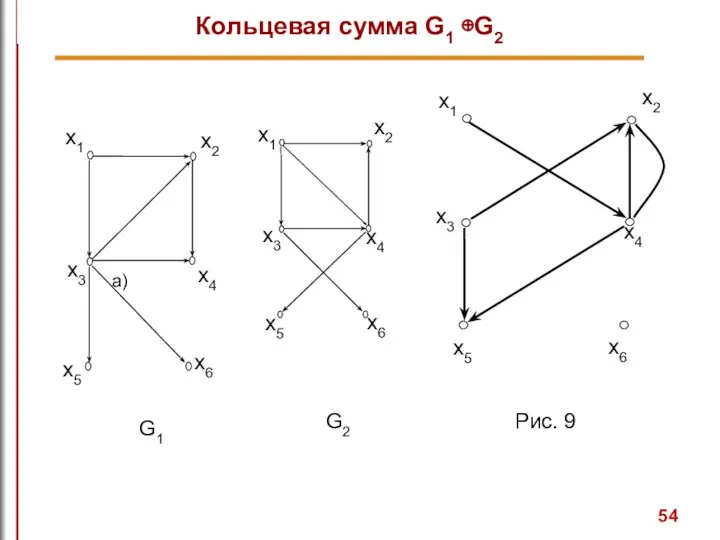
- 53. Кольцевая сумма G1 ⊕G2 Кольцевая сумма двух графов G1 и G2, обозначаемая как G1 ⊕ G2,
- 54. x3 x1 x2 Рис. 9 Кольцевая сумма G1 ⊕G2
- 55. Три рассмотренные операции коммутативны т.е. G1 ∪ G2 = G2 ∪ G1, G1 ∩ G2 =
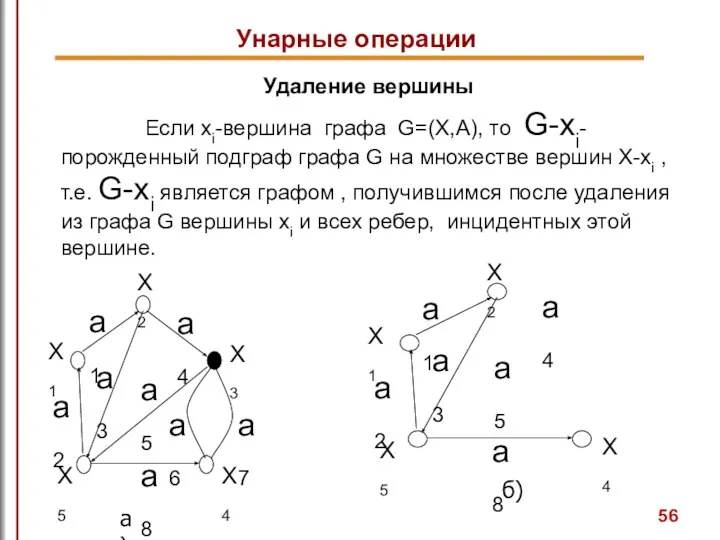
- 56. Удаление вершины Если xi-вершина графа G=(X,A), то G-xi- порожденный подграф графа G на множестве вершин X-xi
- 57. Удаление ребра или дуги Если ai-дуга графа G=(X,A), то G-ai - подграф графа G, получающийся после
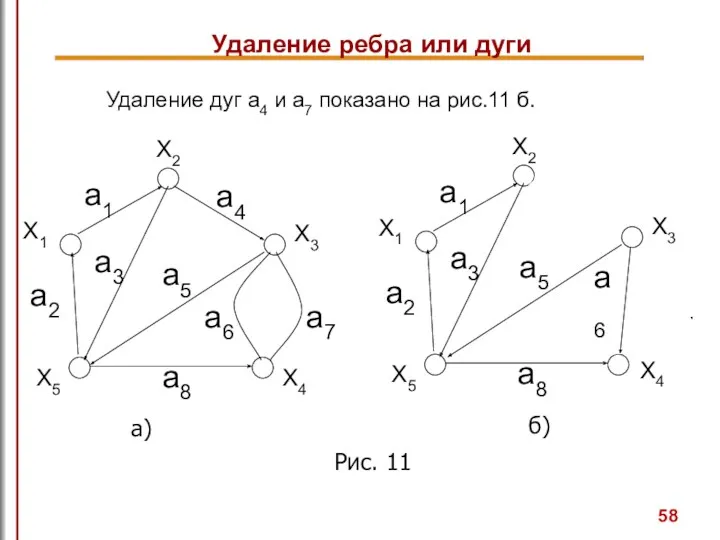
- 58. Рис. 11 Удаление дуг a4 и a7 показано на рис.11 б. Удаление ребра или дуги
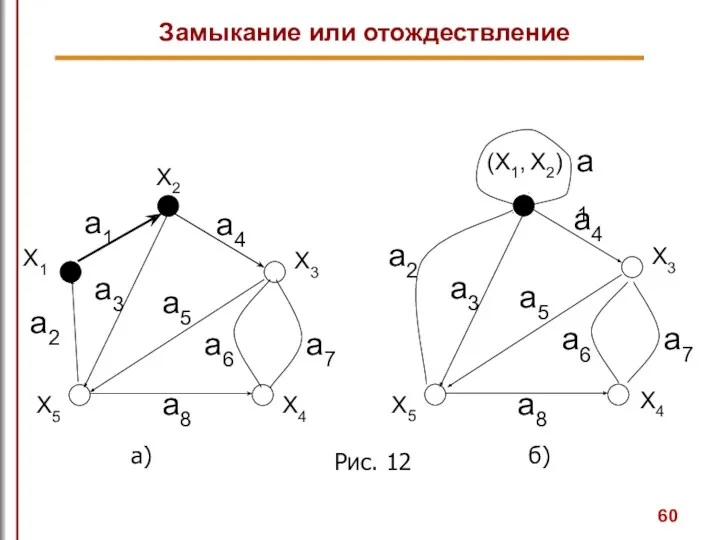
- 59. Замыкание или отождествление Говорят, что пара вершин xi и xj в графе G замыкается (или отождествляется),
- 60. Рис. 12 Замыкание или отождествление
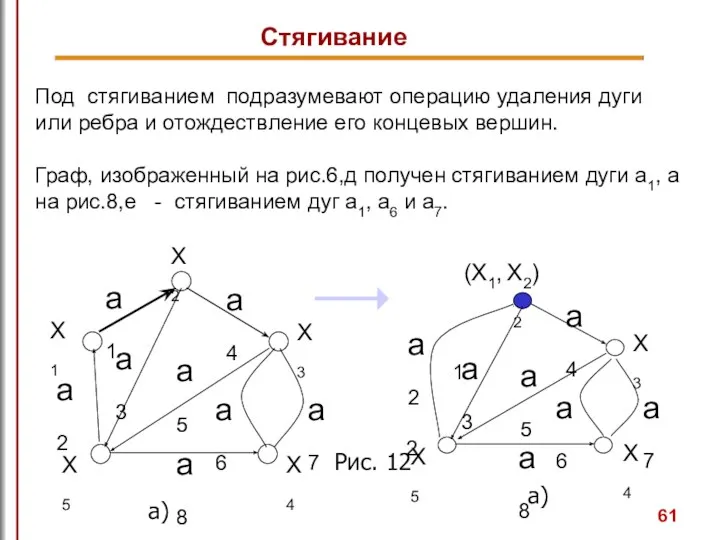
- 61. Рис. 12 Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. Граф,
- 63. Скачать презентацию
























 Математический досуг Весёлые задачи в форме игры КВН для детей подготовительной группы.
Математический досуг Весёлые задачи в форме игры КВН для детей подготовительной группы. Прямая.Отрезок.Луч
Прямая.Отрезок.Луч Замена произведения чисел их суммой
Замена произведения чисел их суммой Метрологические характеристики средств измерительной техники. Лекция 2
Метрологические характеристики средств измерительной техники. Лекция 2 Микрометр. Определение показаний прибора
Микрометр. Определение показаний прибора Вальс цифр!
Вальс цифр! Математика 4 класс
Математика 4 класс Відсотки. Математика. 6 клас
Відсотки. Математика. 6 клас Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32)
Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32) Угол между векторами. Скалярное произведение векторов. 11 класс
Угол между векторами. Скалярное произведение векторов. 11 класс Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ
Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ Статистические методы в научных исследованиях
Статистические методы в научных исследованиях Мир математики. Игра Счастливый случай
Мир математики. Игра Счастливый случай Трапеция. Виды трапеций
Трапеция. Виды трапеций 20231120_skalyarnoe_proizvedenie_vektorov_v_prostranstve
20231120_skalyarnoe_proizvedenie_vektorov_v_prostranstve Понятие корня n-й степени из действительного числа
Понятие корня n-й степени из действительного числа Открытый банк заданий ОГЭ на подобие треугольников
Открытый банк заданий ОГЭ на подобие треугольников Прогрессия вокруг нас. Заключительный урок. 9 класс
Прогрессия вокруг нас. Заключительный урок. 9 класс Методическое пособие по ФЭМП Какую геометрическую фигуру тебе дать?
Методическое пособие по ФЭМП Какую геометрическую фигуру тебе дать? Отношения a : b
Отношения a : b Создание тренажера по подготовке к ОГЭ по математике
Создание тренажера по подготовке к ОГЭ по математике Презентация Путешествие попугая Кеши по стране Математика Диск
Презентация Путешествие попугая Кеши по стране Математика Диск 3 класс Окружность и круг
3 класс Окружность и круг Дії над векторами у просторі. Розв’язування вправ
Дії над векторами у просторі. Розв’язування вправ Проценты
Проценты Итоговое повторение. Алгебра. 8 класс
Итоговое повторение. Алгебра. 8 класс Умножение и деление
Умножение и деление Математический турнир. Команда Великолепная четвёрка
Математический турнир. Команда Великолепная четвёрка