Содержание
- 2. Плоские кривые Пусть кривая целиком лежит в плоскости xOy. Кривая задана: - параметрическое задание кривой (28)
- 3. Плоские кривые Из (29) выразим y: (30) (30) – задание явной функции в виде графика. Вычислим
- 4. Особые точки плоской кривой Определение: точка называется особой точкой плоской кривой, заданной неявным уравнением, если в
- 5. Классификация особых точек плоской кривой Обозначим , и подставим в уравнение (31): (33) продифференцируем по t
- 6. Рассмотрим (33) в особой точке: Классификация особых точек плоской кривой (34) : А. Уравнение (34’) не
- 7. Б. 1) Уравнение (34’) имеет 2 решения. Имеет 2 касательные, следовательно, через точку В. проходит 2
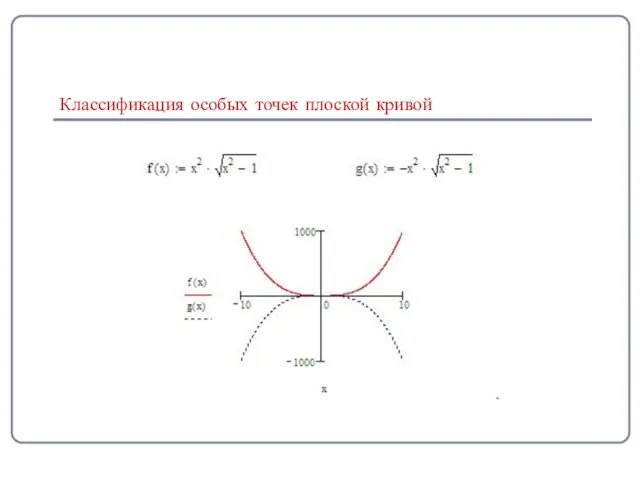
- 8. Классификация особых точек плоской кривой Последние две точки не принадлежат кривой, следовательно, точка (0;0) - особая
- 9. Классификация особых точек плоской кривой
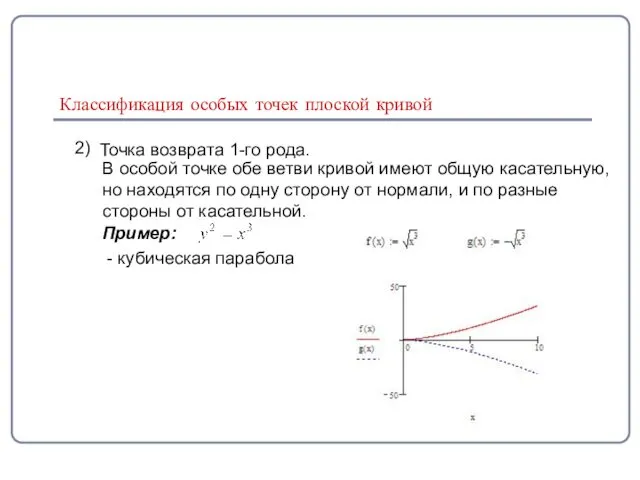
- 10. Классификация особых точек плоской кривой 2) Точка возврата 1-го рода. В особой точке обе ветви кривой
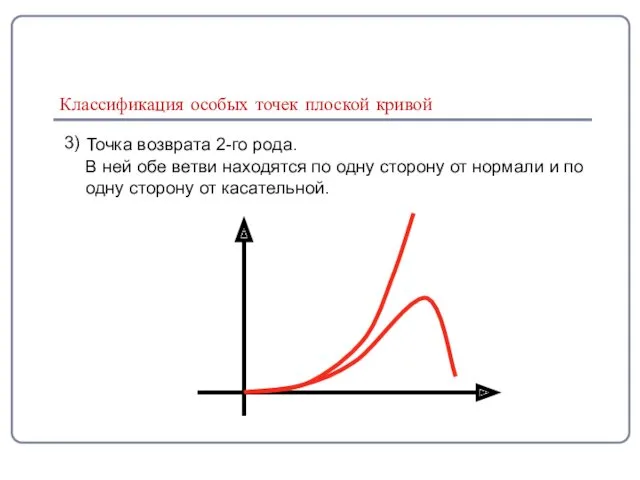
- 11. Классификация особых точек плоской кривой 3) Точка возврата 2-го рода. В ней обе ветви находятся по
- 12. 4) Точка самоприкосновения 5) Классификация особых точек плоской кривой
- 13. Однопараметрическое семейство плоских кривых (ОСПК) Определение: однопараметрическим семейством плоских кривых называется множество кривых на плоскости, удовлетворяющих
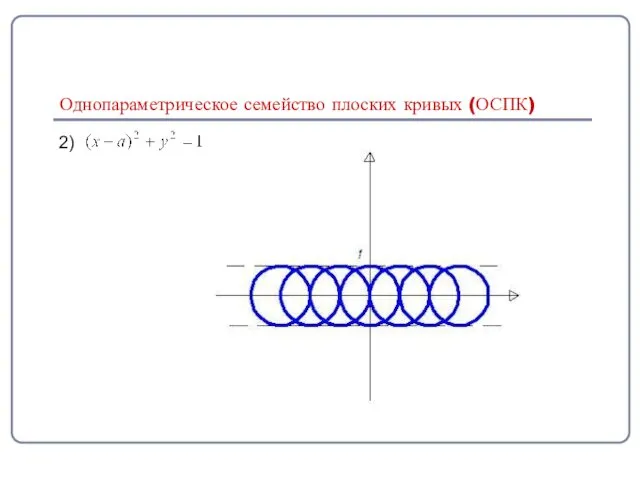
- 14. 2) Однопараметрическое семейство плоских кривых (ОСПК)
- 15. Однопараметрическое семейство плоских кривых (ОСПК) Определение: плоская кривая, которая в каждой своей точке касается некоторой кривой
- 16. Однопараметрическое семейство плоских кривых (ОСПК) Теорема 1. Огибающая ОСПК, если она существует, является дискриминантной кривой этого
- 17. Однопараметрическое семейство плоских кривых (ОСПК) Рассмотрим точку касания некоторой кривой семейства и огибающей, так как кривые
- 18. , следовательно, огибающая удовлетворяет системе уравнений: тогда огибающая есть дискриминантная кривая. Однопараметрическое семейство плоских кривых (ОСПК)
- 19. 2) Пусть - дискриминантная кривая семейства (35). , следовательно, дискриминантная кривая касается в каждой своей точке
- 20. (35) где а – параметр.
- 21. (35) где а – параметр.
- 22. (31)
- 23. Определение: однопараметрическим семейством плоских кривых называется множество кривых на плоскости, удовлетворяющих неявному уравнению: (35) где а
- 24. (31)
- 25. (31)
- 27. Скачать презентацию




















 Использование ИКТ на уроках математики в основной школе как средство активизации познавательной деятельности учащихся
Использование ИКТ на уроках математики в основной школе как средство активизации познавательной деятельности учащихся Маленькая принцесса
Маленькая принцесса Пространство в современной физике
Пространство в современной физике Золотое сечение
Золотое сечение Окружность. Дети. Своя игра
Окружность. Дети. Своя игра Деление на трехзначное число
Деление на трехзначное число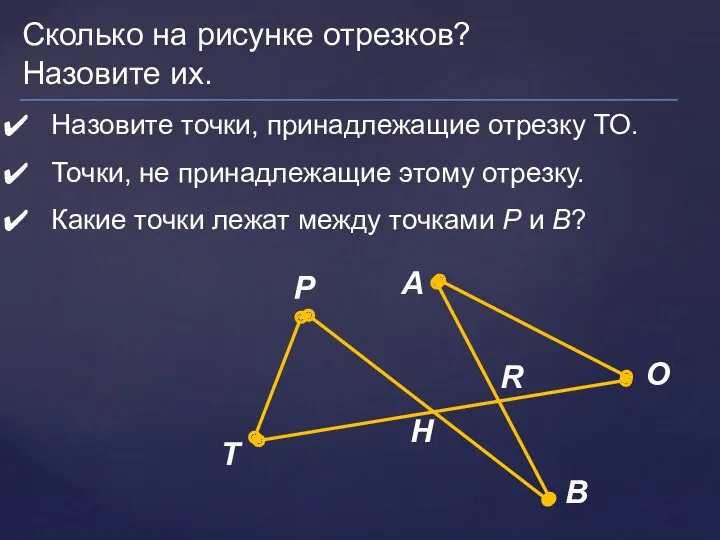 Сравнение отрезков
Сравнение отрезков Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Презентация к уроку математики на тему Сложение и вычитание смешанных чисел
Презентация к уроку математики на тему Сложение и вычитание смешанных чисел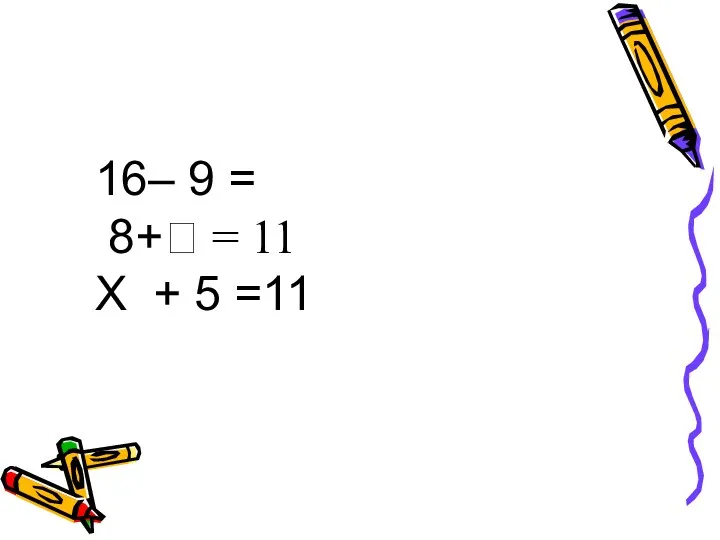 Урок математики во 2 классе Уравнение. Решение уравнений способом подбора
Урок математики во 2 классе Уравнение. Решение уравнений способом подбора Презентация к уроку математики в 1 классе Начальная школа 21 века Что такое умножение
Презентация к уроку математики в 1 классе Начальная школа 21 века Что такое умножение Натуральные числа
Натуральные числа Знаходимо невідомий множник; невідоме ділене або дільник. 2 клас
Знаходимо невідомий множник; невідоме ділене або дільник. 2 клас Решение уравнений. 5 класс
Решение уравнений. 5 класс Ломаные и многоугольники
Ломаные и многоугольники Метр — одиниця довжини
Метр — одиниця довжини Подготовка к введению задач в 2 действия А
Подготовка к введению задач в 2 действия А Презентация к уроку Числовой луч
Презентация к уроку Числовой луч Решение задач по механике с использованием тригонометрии
Решение задач по механике с использованием тригонометрии Обыкновенные дроби. Деление дробей
Обыкновенные дроби. Деление дробей Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Задача линейного программирования. Двойственная задача, двойственный симплекс-метод
Задача линейного программирования. Двойственная задача, двойственный симплекс-метод Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Решение задач 2 класс
Решение задач 2 класс Методика организации математического развития дошкольников 6-7 лет по программе Радуга
Методика организации математического развития дошкольников 6-7 лет по программе Радуга Решение систем уравнений второй степени
Решение систем уравнений второй степени Деление на двузначное число
Деление на двузначное число