Содержание
- 2. Георг Кантор (03.03.1845 - 06.01.1918) немецкий математик.
- 3. Бертран Расселл 18 мая 1872 — 2 февраля 1970 — английский математик, философ и общественный деятель
- 4. Феликс Эдуард Жустин Эмиль Борель (7 января 1871 — 3 февраля 1956) — французский математик и
- 5. Понятие множества Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m
- 6. Введение в теорию множеств 1. Основные определения, терминология Под множеством А мы понимаем совокупность объектов произвольной
- 7. Определение 1 Множество А называется подмножеством В, если для любого х ( ) Обозначение: Теорема 2
- 8. Доказательство Для доказательства а) надо убедиться в истинности высказывания , но оно очевидным образом истинно, так
- 9. Определение 3 Множества А и В называются равными, если они состоят из одних и тех же
- 10. Таким образом, для того, чтобы доказать равенство множеств А и В, надо доказать два включения: и
- 11. 2. Операции над множествами Определение 1 Объединением двух множеств А и В называется множество Пример Пусть
- 12. Объединение множеств Теорема 2 Пусть А, В, С – произвольные множества. Тогда: а) – идемпотентность объединения;
- 13. Доказательство а) Возьмем б) Возьмем в) Возьмем
- 14. г)Возьмем так как высказывание тождественно ложно. Следовательно . д) Пусть то есть, . Значит, высказывание является
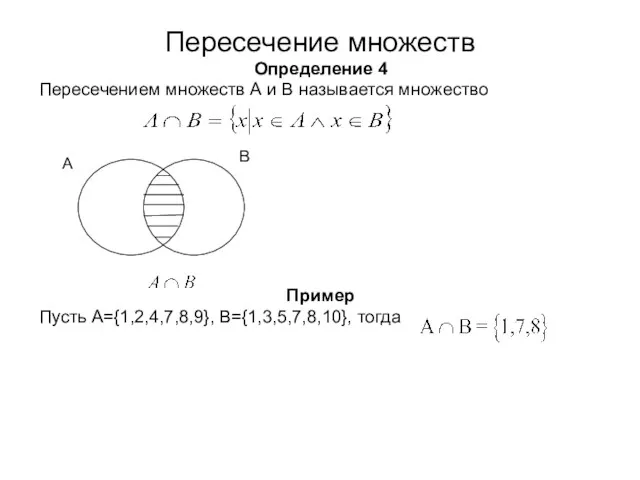
- 15. Пересечение множеств Определение 4 Пересечением множеств А и В называется множество Пример Пусть A={1,2,4,7,8,9}, B={1,3,5,7,8,10}, тогда
- 16. Теорема 5 Пусть А, В, С – произвольные множества, тогда: а) - идемпотентность пересечения; б) -
- 17. Объединение и пересечение множеств Теорема 6 1) 2) 3) 4)
- 18. Разность множеств, дополнение, симметрическая разность Определение 1 Разностью множеств A и B называется множество . Пример
- 19. Разность множеств Теорема 2 Пусть А, В, С – произвольные множества, тогда: 1) 2) 3) 4)
- 20. Множество U назовем "универсальным", если оно содержит все элементы и все множества являются его подмножествами. Понятие
- 21. Дополнение множеств Определение 4 Пусть U – универсальное множество. Дополнением А в U (или просто дополнением
- 22. Дополнение множеств Теорема 5 1) 2) 3) Теорема 6(законы Моргана для дополнений) а) ; б) .
- 24. Скачать презентацию




















 Обозначение натуральных чисел
Обозначение натуральных чисел Округление десятичных чисел
Округление десятичных чисел Золотое сечение
Золотое сечение В царстве формул сокращенного умножения
В царстве формул сокращенного умножения Описательная статистика в Excel. (Лекция 4)
Описательная статистика в Excel. (Лекция 4) Решение уравнений из материалов ЕГЭ по математике
Решение уравнений из материалов ЕГЭ по математике Введение в теорию нечеткой логики
Введение в теорию нечеткой логики Первообразная и интеграл
Первообразная и интеграл Совершенствование навыков решения задач по теме Треугольники
Совершенствование навыков решения задач по теме Треугольники Равносильные уравнения
Равносильные уравнения Единица массы грамм
Единица массы грамм Ознаки зростання і спадання функції
Ознаки зростання і спадання функції Комплексные числа. Решение задач
Комплексные числа. Решение задач Презентация Построй дом к уроку математике по теме Вычитание однозначного числа из двузначного без перехода через разряд
Презентация Построй дом к уроку математике по теме Вычитание однозначного числа из двузначного без перехода через разряд Урок+презентация по математике Путешествие в страну Математики для 5 класса
Урок+презентация по математике Путешествие в страну Математики для 5 класса Призма. Прямая и наклонная призма. Параллелепипед. Куб
Призма. Прямая и наклонная призма. Параллелепипед. Куб Числовые и буквенные выражения
Числовые и буквенные выражения Көпбұрыш, тіктөртбұрыш, шаршы, дөңгелек
Көпбұрыш, тіктөртбұрыш, шаршы, дөңгелек Математическая конкурс-игра для обучающихся 9 класса
Математическая конкурс-игра для обучающихся 9 класса Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника Умножение дробей. Знакомство с друзьями из Британии
Умножение дробей. Знакомство с друзьями из Британии Решение комбинаторных задач
Решение комбинаторных задач Чтение и запись десятичных дробей
Чтение и запись десятичных дробей Практико-ориентированные задачи на ОГЭ №1-5
Практико-ориентированные задачи на ОГЭ №1-5 презентация к уроку математики Число 10.
презентация к уроку математики Число 10. Об особенностях подготовки к ЦТ по математике
Об особенностях подготовки к ЦТ по математике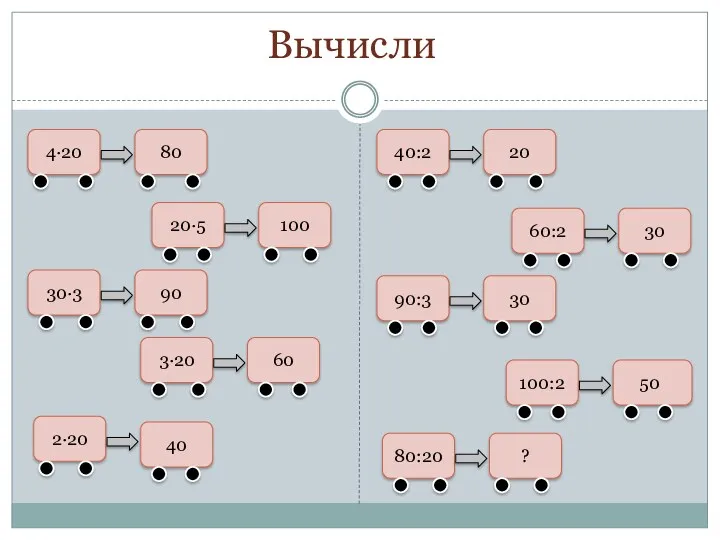 Делние на круглое число.
Делние на круглое число. Проценты в школьном курсе математики
Проценты в школьном курсе математики