Содержание
- 2. Определение. Численные методы это методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над ними,
- 3. Погрешность округлений. При выполнении арифметических операций над числами, при вводе и выводе данных производится округление. Погрешность
- 4. 2. Погрешность численного решения задачи Введем некоторые переменные. x* − точное значение вычисляемого параметра;
- 5. Чтобы численный метод считался удачно выбранным, необходимо выполнение некоторых условий: А также должно выполняться условие: ρ0
- 6. Определение. Число а называется приближенным значением по недостатку, если оно меньше истинного значения, и по избытку,
- 7. Определение. Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре:
- 8. А = 3,1415926 − округляют до двух знаков после запятой: а = 3,14. Δ a =
- 9. Следовательно, приближенное значение числа А в пункте b) является более точным. При сложении и вычитании приближенных
- 10. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ 1. Общая постановка задачи Пусть дано уравнение f(x) = 0, где f(x) −
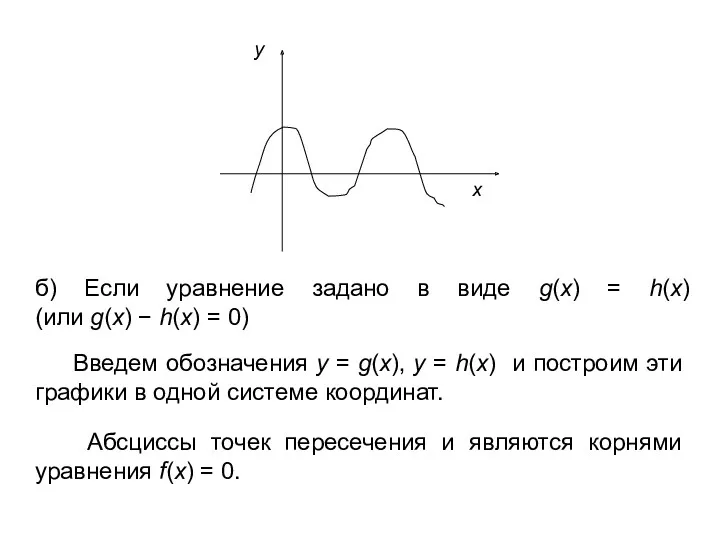
- 11. б) Если уравнение задано в виде g(x) = h(x) (или g(x) − h(x) = 0) Введем
- 12. II. Определение отрезка. На выбранном отрезке [a, b] находится один корень уравнения f(x) = 0.
- 13. 2. МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ Рассмотрим несколько методов решения уравнений с одной переменной. а)
- 14. Будем называть отрезок [a, b] промежутком существования корня, а точку с − пробной точкой. Обозначим a
- 15. Таким образом из этих двух отрезков выбирают тот, на концах которого функция имеет значения разных знаков.
- 16. В качестве приближенного значения корня берем середину отрезка [an, bn] x* − точное значение корня cn
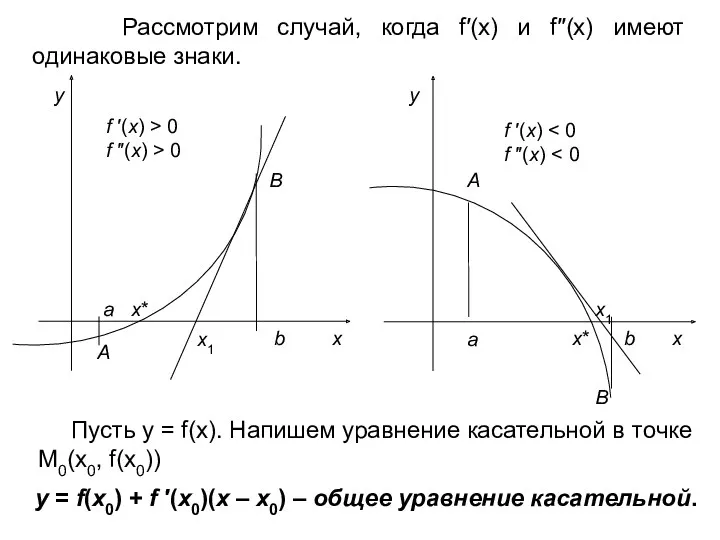
- 17. б) метод касательных (метод Ньютона) Пусть действительный корень уравнения f(x) = 0 изолирован на отрезке [a,
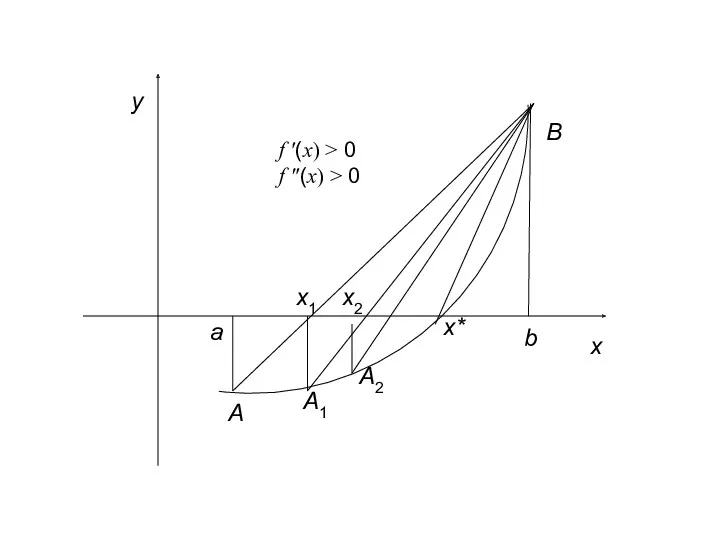
- 18. Рассмотрим случай, когда f′(x) и f′′(x) имеют одинаковые знаки. Пусть у = f(x). Напишем уравнение касательной
- 19. Подставим точку М1(x1, 0) в уравнение касательной: 0 = f(x0) + f′(x0)(x1 – x0) f′(x0)(x1 –
- 20. 0 = f(x1) + f ′(x1)(x2 – x1) f ′(x1)(x2 – x1) = – f(x1) Полученная
- 21. Правила выбора исходной точки x0: За исходную точку х0 следует выбирать тот конец отрезка [a, b],
- 22. так как x* – точное значение корня уравнения f(x) = 0, то f(x*) = 0 ⇒
- 23. в) метод хорд Метод заключается в том, что дуга графика функции f(x) = 0 на отрезке
- 25. Напишем общее уравнение прямой, проходящей через две точки М1(x1, y1) и М2(x2, y2): (М1М2): Используя это
- 26. Проведем хорду через точки А(х1, f(х1)) и B(b, f(b)): возьмем точку пересечения хорды с осью (ох)
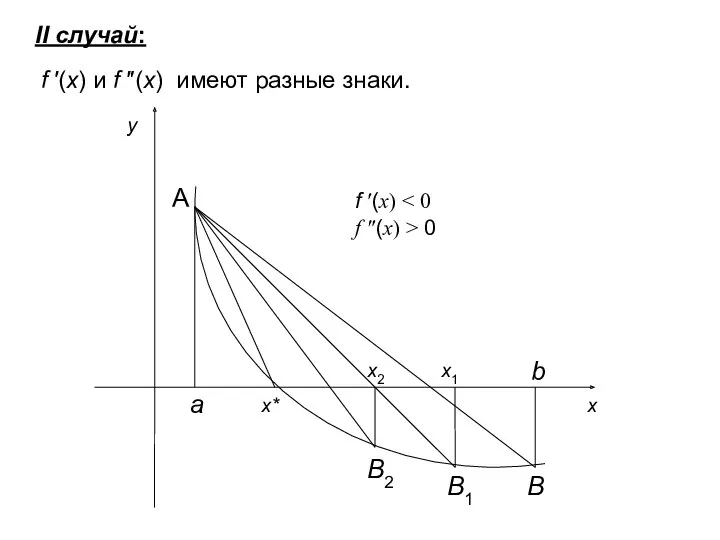
- 27. II случай: f ′(x) и f ″(x) имеют разные знаки. A
- 28. , у = 0, x = x1 , отсюда , или Проведем хорду через точки А(a,
- 29. Полученная таким образом последовательность x0, x1, x2, … имеет своим пределом искомый корень. Вывод: В качестве
- 30. г) комбинированное применение методов хорд и касательных Необходимо найти действительный корень уравнения f(x) = 0, изолированный
- 31. Величины x11 и x12 принадлежат промежутку изоляции, причем f(x11) и f(x12) имеют разные знаки. Построим новую
- 32. Каждая из последовательностей x11, x21, x31, …, xn1, … и x12, x22, x32, …, xn2, …
- 33. ТЕМА 3. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ §1. Постановка задачи Рассмотрим систему из n линейных уравнений с
- 34. §2. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ I. Точные (Прямые) методы Точные (Прямые) методы – это методы,
- 35. – вектор (столбец) неизвестных; – вектор (столбец) свободных членов. Потребуем от системы выполнение определенных условий: 1.
- 36. Тогда при небольших n можем использовать формулы Крамера: , (i = 1, 2, 3, … ,
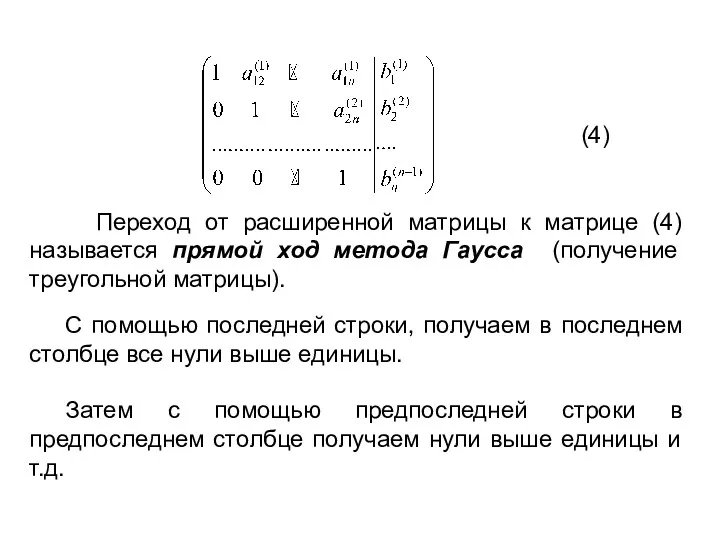
- 37. б) Метод Гаусса. Последовательное исключение неизвестных. Выпишем расширенную матрицу. (3) Предположим, что коэффициент a11, называемый ведущим
- 38. ~ С помощью первой строки получаем в первом столбце, начиная со второй строки, нули. Для этого,
- 39. ~ ~ С помощью второй строки получаем во втором столбце ниже единицы все нули. Получаем ~
- 40. (4) Переход от расширенной матрицы к матрице (4) называется прямой ход метода Гаусса (получение треугольной матрицы).
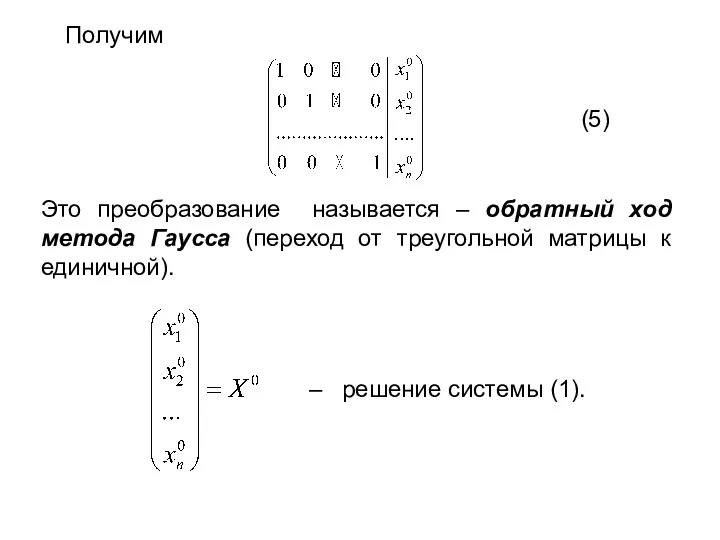
- 41. Получим Это преобразование называется – обратный ход метода Гаусса (переход от треугольной матрицы к единичной). (5)
- 42. в) Метод Гаусса с выбором главного элемента Рассмотренный выше простейший вариант метода Гаусса, называемый схемой единственного
- 43. Затем во втором столбце среди элементов, начиная со второго, выбираем наибольший по модулю элемент и строку,
- 44. ε1 = |a11 x10 + a12 x20 + … + a1n xn0 – b1| По малости
- 45. II. Итерационные методы Итерационные методы – это методы, в которых точное решение может быть получено лишь
- 46. Обозначим (6) Система (6) приведена к нормальному виду. Запишем ее в матричном виде: X = β
- 47. х0 = β – нулевое приближение. Общая формула имеет вид: Будем решать систему (6) методом последовательных
- 48. Если последовательность приближений имеет предел, то – точное решение системы (6) следовательно, системы (1). Теорема 2.
- 49. – k-ое приближенное значение неизвестных, вычисленных по методу итераций. Тогда | xi(k+1) – xi(k) | Оценка
- 50. Пример. Показать, что для данной системы итерационный процесс сходится и определить, сколько итераций следует выполнить, чтобы
- 51. ||β|| = 0,41, (k + 1) lg 0,55 + lg 0,41 – lg 0,45 (k +
- 52. б) метод Зейделя. Пусть дана система линейных уравнений Ax = b, (7) Если i-ое уравнение системы
- 53. Метод Зейделя состоит в том, что итерации производятся по формуле (9) Итерации (9) по методу Зейделя
- 54. Сформулируем теорему о двух различных достаточных условиях сходимости метода Зейделя. Теорема 3. Для существования единственного решения
- 55. ТЕМА 4. ЧИСЛЕННАЯ ИНТЕРПОЛЯЦИЯ §1. Интерполяционные многочлены Пусть в точках x0, x1, …, xn заданы значения
- 56. Часто для решения этой задачи строится алгебраический многочлен Ln(x) степени n, значения которого в точках xi
- 57. Например, если fi = 0, i = 0, 1, …, n, то интерполяционный многочлен Ln(x) ≡
- 58. §2. ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА Терема 1. Существует единственный интерполяционный многочлен n-ой степени, удовлетворяющий условиям (1). Доказательство.
- 59. и, наконец, в общем случае при любом натуральном n (5) где (6) (i = 0, 1,
- 60. Аналогично, формула (4) задает некоторый многочлен L2(x) второй степени, удовлетворяющий при n = 2 условиям (1).
- 61. Докажем единственность интерполяционного многочлена. (7) Тогда согласно (1) и (7) (8)
- 62. Теорема 1 полностью доказана. Интерполяционный многочлен, представленный в виде (5), называется интерполяционным многочленом Лагранжа, а функции
- 63. §3. ПОГРЕШНОСТЬ ИНТЕРПОЛЯЦИИ Запишем равенство f(x) = Ln(x) + Rn(x), где Rn(x) – остаточный член, т.е.
- 64. (11) где и оценка максимальной погрешности интерполяции на всем отрезке [a, b]: (12)
- 65. §4. Интерполяционный многочлен Ньютона Предположим, что узлы интерполяции отстоят друг от друга на одинаковом расстоянии x0,
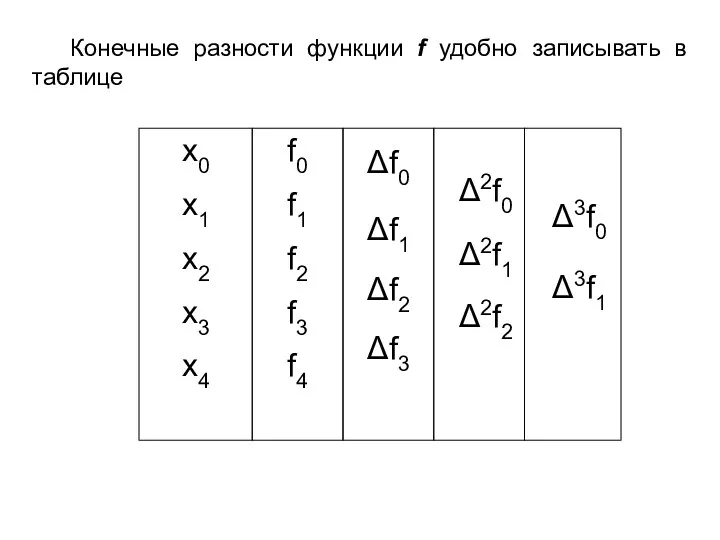
- 66. Определение. Пусть xk = x0 + k⋅h, где k – целое, h > 0, fk =
- 67. Конечные разности функции f удобно записывать в таблице x0 x1 x2 x3 x4 f0 f1 f2
- 68. Пусть x0, x1 = x0 + h, x2 = x0 + 2h, … xk = x0
- 69. Pn(x2) = a0+ a1(x2 – x0) + a2(x2 – x0)(x2 – x1) = y2 2h2 a2
- 70. Pn(x3) = a0+ a1(x3 – x0) + a2(x3 – x0)(x3 – x1) + + a3(x3 –
- 71. Таким образом, формула Ньютона для интерполирования вперед имеет вид (2)
- 72. §5. ИНТЕРПОЛИРОВАНИЕ НАЗАД Интерполяционный многочлен с узлами x0, x –1 , …, x –n, где x
- 73. x-4 x-3 x-2 x-1 x0 f-4 f-3 f-2 f-1 f0 Δf-4 Δf-3 Δf-2 Δf-1 Δ2f-4 Δ2f-3
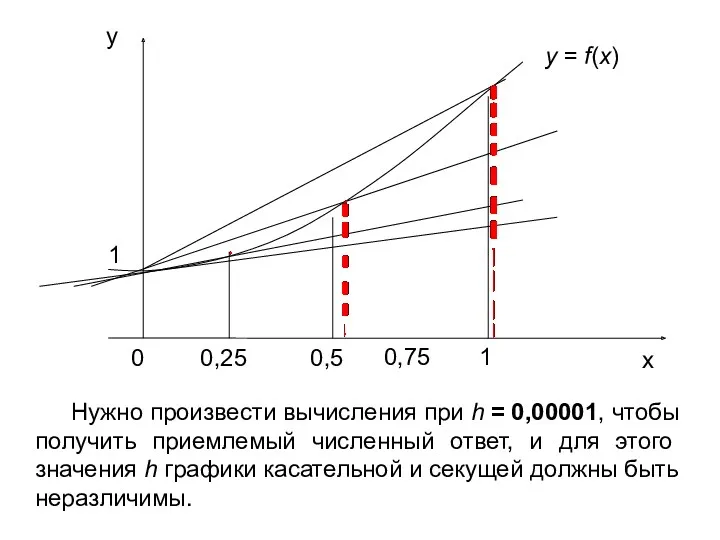
- 74. §6. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ Рассмотрим численный процесс приближения производной f(x): (1) Выберем последовательность {hk} так, что hk
- 75. Будем вычислять только конечное количество членов D1, D2, …, Dn последовательности (2). Следовательно, для ответа следует
- 76. Нужно произвести вычисления при h = 0,00001, чтобы получить приемлемый численный ответ, и для этого значения
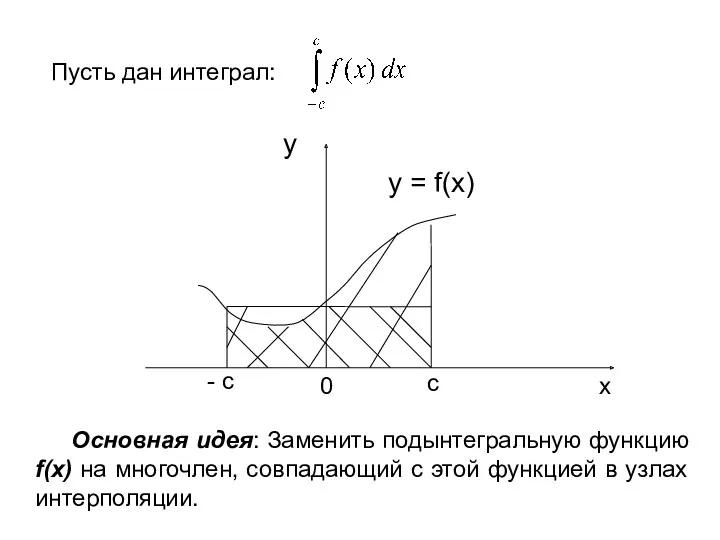
- 77. ТЕМА 5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ §1. Приближенные методы вычислений определенных интегралов Однако, вычисление по этой формуле не
- 78. Основная идея: Заменить подынтегральную функцию f(x) на многочлен, совпадающий с этой функцией в узлах интерполяции.
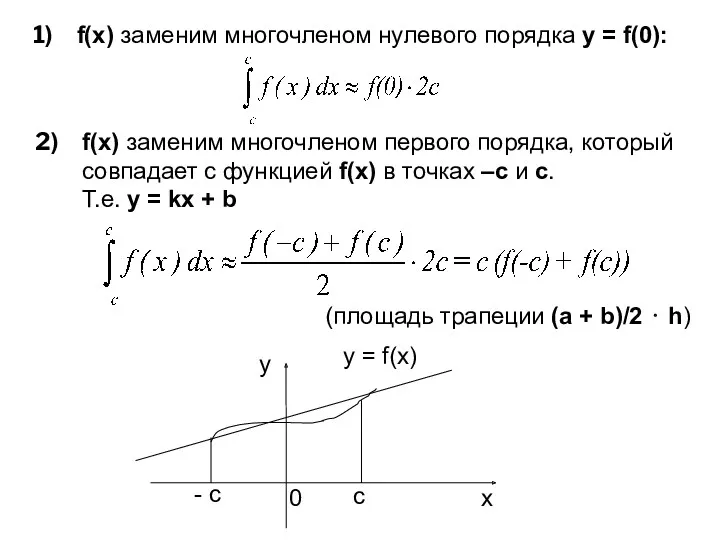
- 79. f(x) заменим многочленом нулевого порядка y = f(0): f(x) заменим многочленом первого порядка, который совпадает с
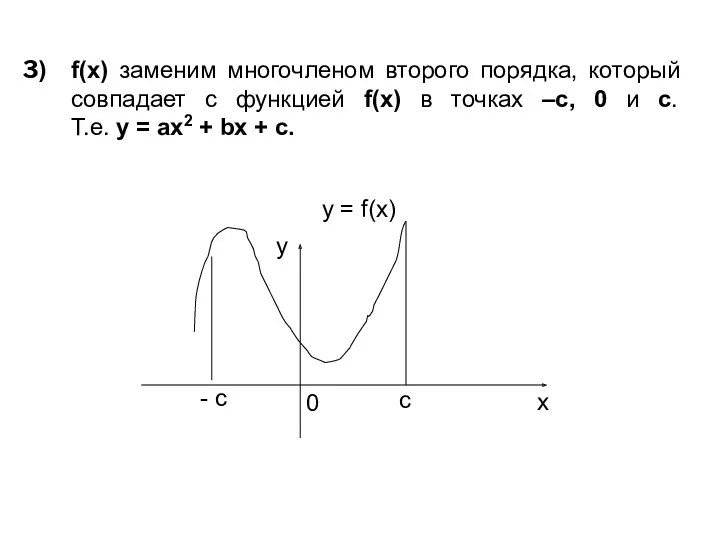
- 80. f(x) заменим многочленом второго порядка, который совпадает с функцией f(x) в точках –с, 0 и с.
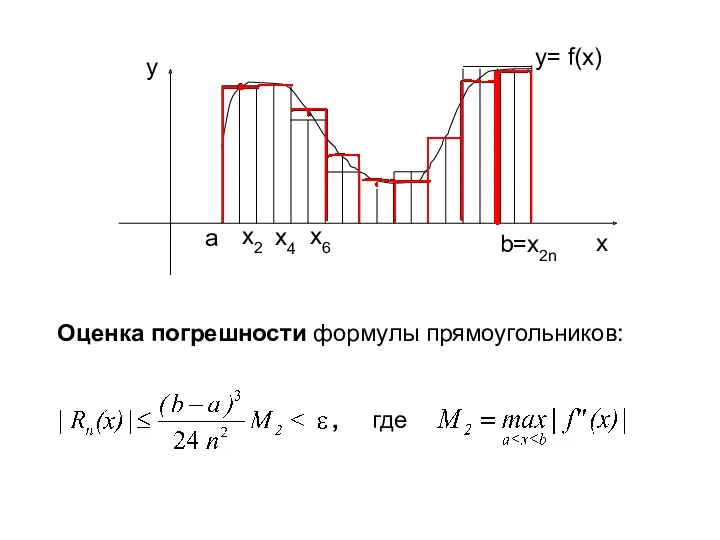
- 81. Метод прямоугольников Формулы прямоугольников имеют вид: или
- 82. Однако для удобства вычислений поступают следующим образом: Точку x1 выбирают таким образом, чтобы она являлась серединой
- 83. Оценка погрешности формулы прямоугольников:
- 84. Метод трапеций
- 85. Вывод: – формула трапеций. Оценка погрешности формулы трапеций.
- 86. 3) Метод парабол (Симпсона). Отрезок интегрирования [a, b] разобьем на 2n равных частей: a = x0
- 88. тогда на промежутке [x0, x2] имеем:
- 90. Вывод: Оценка погрешности формулы парабол: где
- 91. §2. Формулы Ньютона-Котеса Делим отрезок [a, b] на n равных частей. – квадратурная формула Ньютона-Котеса, –
- 92. Эти формулы определяют семейство квадратурных формул. Параметром этого семейства является число n – степень интерполяционного многочлена,
- 93. Пусть n=1, т.е. имеется всего две точки x0 и x1=x0 + h, в которых известны значения
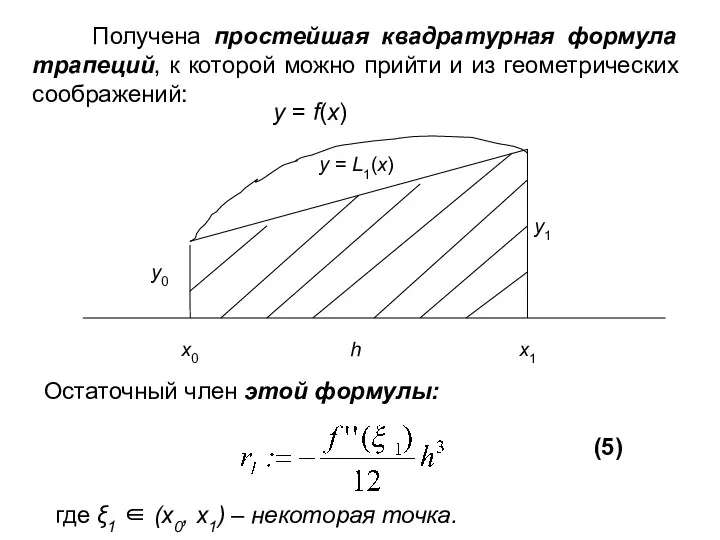
- 94. Получена простейшая квадратурная формула трапеций, к которой можно прийти и из геометрических соображений: Остаточный член этой
- 95. Положим в (3) n = 2, т.е. проинтерполируем функцию f(x) по трем точкам: x0, x1 =
- 96. Предполагая теперь n = k, мы придем к частным формулам Ньютона-Котеса: (6)
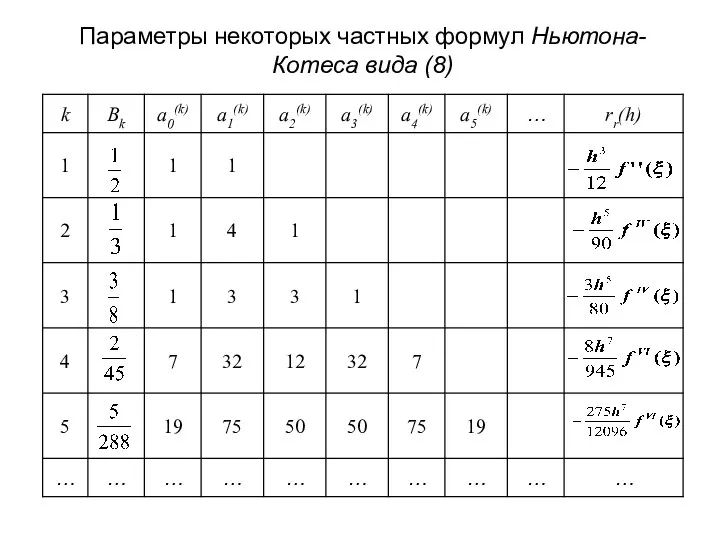
- 97. Параметры некоторых частных формул Ньютона-Котеса вида (8)
- 98. §3. КВАДРАТУРНАЯ ФОРМУЛА ГАУССА Общий вид линейной квадратурной формулы – это (8) где фиксированные аргументы xi
- 99. Все рассмотренные выше квадратурные формулы характерны тем, что узла в них брались равноотстоящими с шагом h,
- 100. Далее откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. В таком случае целесообразно
- 101. т.е. строить квадратурные формулы вида (10) от которых на основе (9) легко перейти к квадратурным формулам
- 103. Скачать презентацию









![II. Определение отрезка. На выбранном отрезке [a, b] находится один корень уравнения f(x) = 0.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-11.jpg)

![Будем называть отрезок [a, b] промежутком существования корня, а точку](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-13.jpg)

![В качестве приближенного значения корня берем середину отрезка [an, bn]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-15.jpg)





























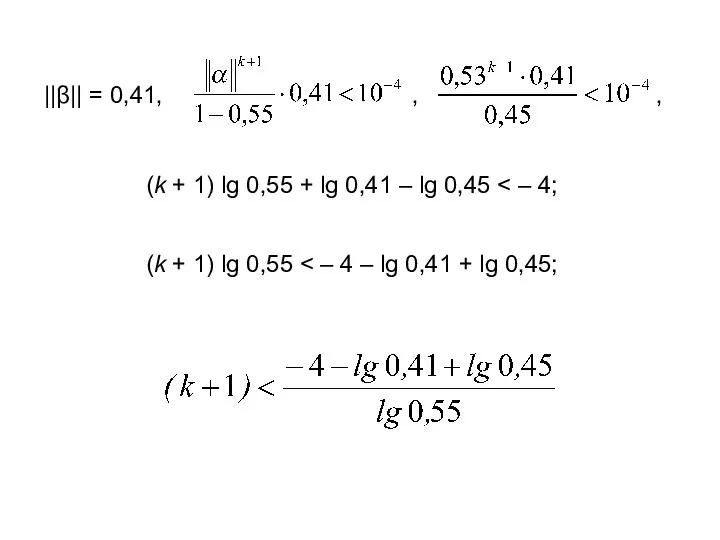












![(11) где и оценка максимальной погрешности интерполяции на всем отрезке [a, b]: (12)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-63.jpg)



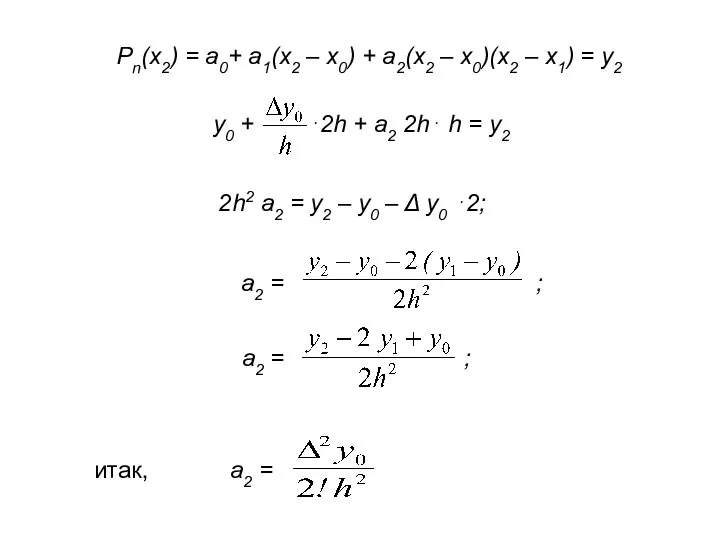
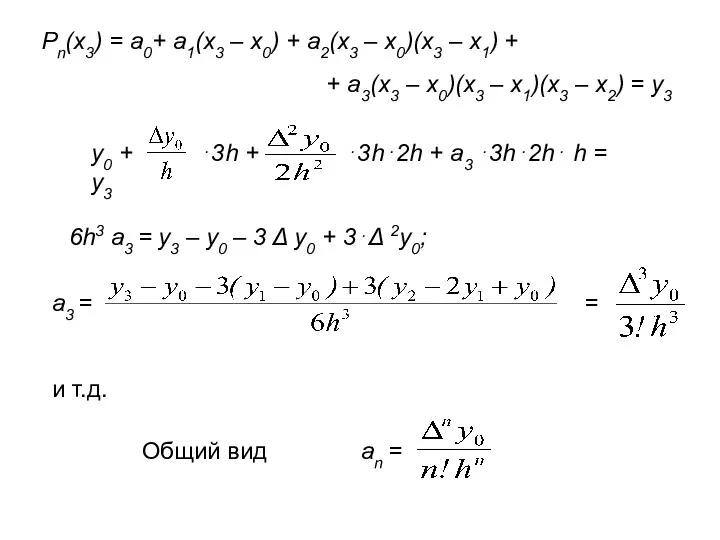










![3) Метод парабол (Симпсона). Отрезок интегрирования [a, b] разобьем на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-85.jpg)
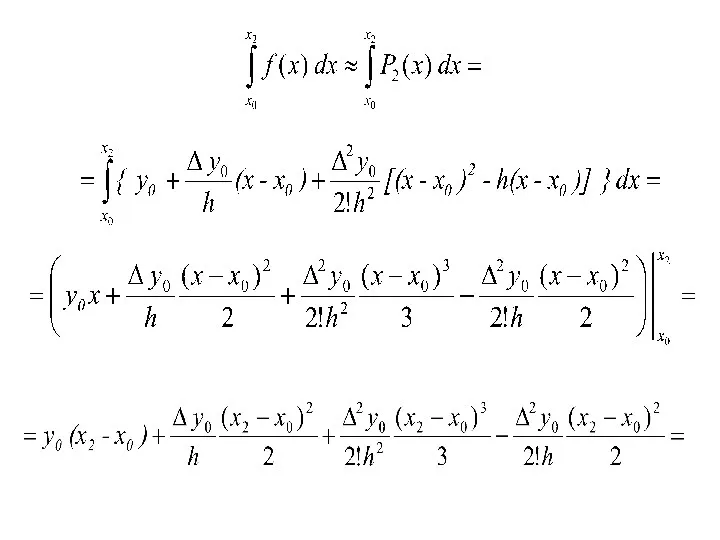
![тогда на промежутке [x0, x2] имеем:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-87.jpg)
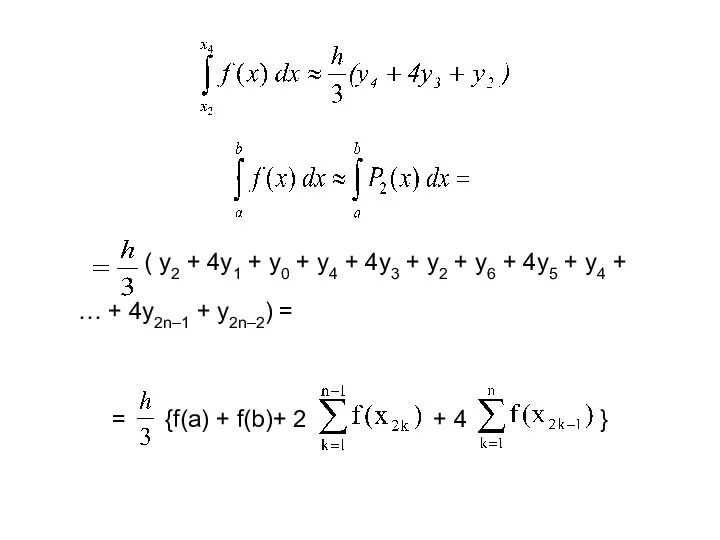

![§2. Формулы Ньютона-Котеса Делим отрезок [a, b] на n равных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/590577/slide-90.jpg)








 презентация для уроков литературного чтения
презентация для уроков литературного чтения Вспоминаем, повторяем
Вспоминаем, повторяем Устный счёт 4 класс
Устный счёт 4 класс Статистическое изучение динамики социально-правовых явлений и процессов
Статистическое изучение динамики социально-правовых явлений и процессов Решение задач с величинами.
Решение задач с величинами. Умножение на два. Тренажёр помоги рыбке. (2 класс)
Умножение на два. Тренажёр помоги рыбке. (2 класс) Логикалық операциялар (дизъюнкция, конъюнкция, инверсия)
Логикалық операциялар (дизъюнкция, конъюнкция, инверсия) Графики функции у=2х
Графики функции у=2х Задачи на увеличение и уменьшение числа на несколько единиц
Задачи на увеличение и уменьшение числа на несколько единиц Сечение многогранников
Сечение многогранников Устная и письменная нумерация чисел в пределах 1000
Устная и письменная нумерация чисел в пределах 1000 Векторы. Откладывание вектора от данной точки
Векторы. Откладывание вектора от данной точки 5 саны және цифры
5 саны және цифры Факториальные кольца
Факториальные кольца Производная. Понятие о производной
Производная. Понятие о производной Старинные русские меры длины
Старинные русские меры длины 6. Уравнение окружности
6. Уравнение окружности Магические квадраты
Магические квадраты Математика в Древнем Египте
Математика в Древнем Египте Фокусы в математике
Фокусы в математике Единицы массы. Килограмм
Единицы массы. Килограмм Случайные величины
Случайные величины Нормальный алгоритм Маркова. Лекция №4
Нормальный алгоритм Маркова. Лекция №4 Цилиндр. Геометрия 11 класс
Цилиндр. Геометрия 11 класс Прямая на плоскости
Прямая на плоскости Задачи на движение
Задачи на движение Правильные и неправильные дроби
Правильные и неправильные дроби Статистичні показники
Статистичні показники