- Главная
- Математика
- Теория принятия решений. Матричные игры, пример решения

Содержание
- 2. В качестве активных стратегий игрока P1 можно выбрать две чистых стратегии, соответствующие прямым, пересекающимся в N.
- 3. ПРИМЕР 9 А1 : 4y + 3 (1 – y) = Z A2 : 2y +
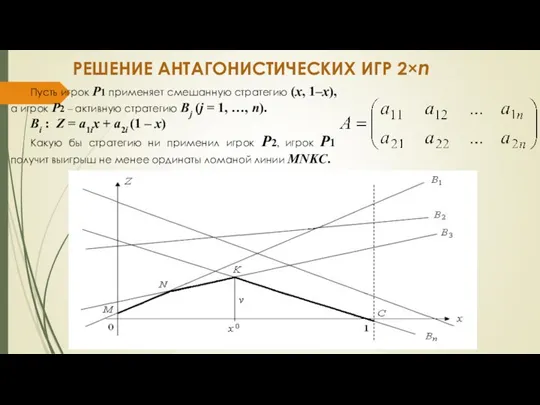
- 4. РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ ИГР 2×n Пусть игрок P1 применяет смешанную стратегию (х, 1–х), а игрок P2 –
- 5. Оптимальная стратегия игрока P1: Х0 = (x0, (1 – x0)) Цена игры V равна ординате точки
- 6. ПРИМЕР 10 В1 : 2x + 4 (1 – x) = Z В2 : 3x +
- 8. Скачать презентацию
В качестве активных стратегий игрока P1 можно выбрать две чистых стратегии,
В качестве активных стратегий игрока P1 можно выбрать две чистых стратегии,
Оптимальную смешанную стратегию игрока P1: X0 = (х0, (1 – х0)) можно определить как для игры 2×2
Х0 = (0, …, 0, х0, 0, …, 0, 1 – х0, 0, …, 0)
i-я компонента j-я компонента
ПРИМЕР 9
А1 : 4y + 3 (1 – y) = Z
A2
ПРИМЕР 9
А1 : 4y + 3 (1 – y) = Z
A2
A3 : 5 (1 – y) = Z
A4 : –y + 6 (1 – y) = Z
В точке N пересекаются прямые
А1 и А4
4y + 3 (1 – y) = –y + 6 (1 – y)
y0 = 3/8, Y 0 = (3/8, 5/8)
V = 27/8
В1 : 4x0 – (1 – x0) = V
В2 : 3x0 + 6 (1 – x0) = V
4x0 – (1 – x0) = 3x* + 6 (1 – x0)
x0 = 7/8, 1 – x0 = 1/8
Х 0 = (7/8, 0, 0, 1/8)
РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ ИГР 2×n
Пусть игрок P1 применяет смешанную стратегию (х, 1–х),
РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ ИГР 2×n
Пусть игрок P1 применяет смешанную стратегию (х, 1–х),
Вi : Z = a1ix + a2i (1 – x)
Какую бы стратегию ни применил игрок P2, игрок P1 получит выигрыш не менее ординаты ломаной линии MNKC.
Оптимальная стратегия игрока P1: Х0 = (x0, (1 – x0))
Цена игры
Оптимальная стратегия игрока P1: Х0 = (x0, (1 – x0))
Цена игры
В качестве активных стратегий игрока P2 можно выбрать две чистых стратегии, соответствующих любым двум прямым, пересекающимся в точке К. Пусть это Вi и Вj
Оптимальную смешанную стратегию игрока P2 найти как в игре 2×2
Y 0 = (0, …, 0, у0, 0, …, 0, 1 – у0, 0, …, 0)
i-я компонента j-я компонента
ПРИМЕР 10
В1 : 2x + 4 (1 – x) = Z
В2 : 3x
ПРИМЕР 10
В1 : 2x + 4 (1 – x) = Z
В2 : 3x
В3 : x + 3 (1 – x) = Z
В4 : 4x + (1 – x) = Z
В точке N пересекаются прямые В3 и В4,
x + 3 (1 – x) = 4x + (1 – x)
x0 = 2/5, Х 0 = (2/5, 3/5)
V = 11/5
Активными стратегиями игрока P2 будут В3 и В4,
А1 : y + 4 (1 – y) = Z
A2 : 3y + (1 – y) = Z
y0 = 3/5 Y 0 = (0, 0, 3/5, 2/5)




 Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их числовые характеристики
Формула полной вероятности, формула Байеса. Схема Бернулли. Понятия дискретной и непрерывной величин, их числовые характеристики Прямоугольный треугольник. 7 класс
Прямоугольный треугольник. 7 класс Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Дії з іменованими числами. Дистанційне навчання
Дії з іменованими числами. Дистанційне навчання Прямоугольные треугольники. Свойства прямоугольных треугольников
Прямоугольные треугольники. Свойства прямоугольных треугольников Математические головоломки
Математические головоломки Формулы сокращенного умножения. Тест. 7 класс
Формулы сокращенного умножения. Тест. 7 класс Свойства степени с натуральным показателем. Урок по алгебре в 7 классе
Свойства степени с натуральным показателем. Урок по алгебре в 7 классе Математический КВН для 3 класса
Математический КВН для 3 класса Счет в пределах 10. Игра Бабочки
Счет в пределах 10. Игра Бабочки 20231108_zadanie_21
20231108_zadanie_21 Презентация к уроку математики по теме Площадь прямоугольника 3класс
Презентация к уроку математики по теме Площадь прямоугольника 3класс Самостоятельная математическая деятельность детей дошкольного возраста
Самостоятельная математическая деятельность детей дошкольного возраста Семинар-практикум Значение логико-математических игр в умственном развитии детей старшего дошкольного возраста
Семинар-практикум Значение логико-математических игр в умственном развитии детей старшего дошкольного возраста Математический зоопарк
Математический зоопарк Презентация к уроку математики в 1 классе
Презентация к уроку математики в 1 классе Презентация Число 9, фифра 9
Презентация Число 9, фифра 9 Диференціальне числення функції однієї змінної
Диференціальне числення функції однієї змінної Решение неравенств методом интервалов
Решение неравенств методом интервалов Происхождение математических знаков
Происхождение математических знаков Изображение объема на плоскости. Линейная перспектива
Изображение объема на плоскости. Линейная перспектива Числа от 11 до 20
Числа от 11 до 20 Задачи по комбинаторике
Задачи по комбинаторике Тайны чисел. Творческая работа
Тайны чисел. Творческая работа Основное свойство дроби
Основное свойство дроби Объём шара и его частей
Объём шара и его частей Основные понятия комбинаторики. Формулы перестановки, сочетания и размещения элементов во множестве
Основные понятия комбинаторики. Формулы перестановки, сочетания и размещения элементов во множестве Математика и здоровье
Математика и здоровье