Содержание
- 2. Теория рядов широко используется в теоретических исследованиях различных вопросах естествознания и в приближенных вычислениях. С помощью
- 3. В частности, программы приближенного вычисления значений элементарных функций и решения многих стандартных задач, заложенные в память
- 4. 1. ЧИСЛОВЫЕ РЯДЫ. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ.
- 5. 1.1. Понятие о рядах Выражение вида называется числовым рядом. - члены ряда - общий член ряда
- 6. Сумма n первых членов ряда называется n-ой частичной суммой ряда и обозначается через частичные суммы
- 7. При изменении n меняется и Sn; при этом возможны два случая: 1) величина Sn при n→∞
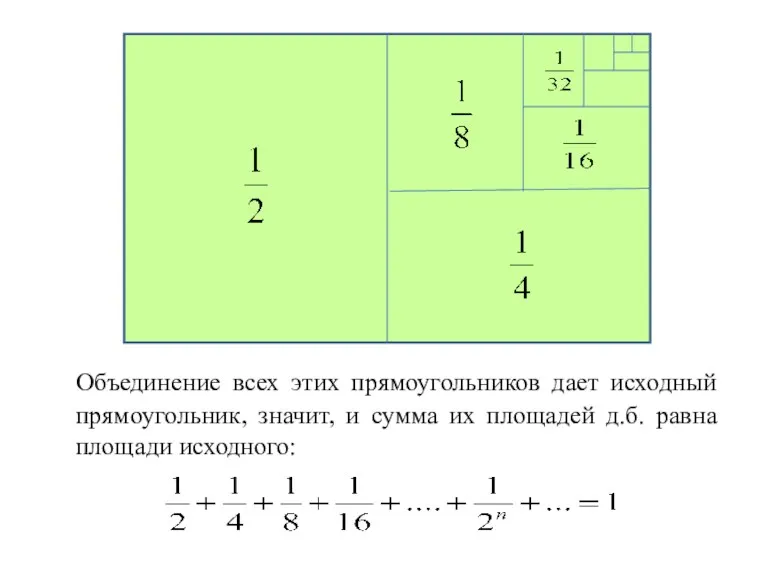
- 8. Пример 1 (бесконечно убывающая геометрическая прогрессия): частичные суммы всё меньше и меньше отличаются от 1.
- 9. Объединение всех этих прямоугольников дает исходный прямоугольник, значит, и сумма их площадей д.б. равна площади исходного:
- 10. Ряд сходится, т.к. формула для геометрической прогрессии
- 11. Пример 2 (бесконечно возрастающая геометрическая прогрессия): Ряд расходится, т.к формула для геометрической прогрессии
- 12. Ряд геометрической прогрессии Ряд сходится при Ряд расходится при ( см.пример 1) (см. пример 2)
- 13. Пример 3 (гармонический ряд): Ряд расходится.
- 14. Пример 4 последовательность частичных сумм не имеет предела Ряд расходится.
- 15. Пример 5 Ряд сходится к . Сумму ряда нашёл Г.Лейбниц Пример 6 Ряд сходится к .
- 16. Свойства конечных сумм , такие как ассоциативность (произвольная группировка членов), коммутативность (произвольная перестановка членов), для рядов
- 17. Свойства рядов 10. Если ряд сходится и его сумма равна S, то ряд также сходится и
- 18. 10. Если ряд расходится и с≠0, то ряд также расходится.
- 19. Пример 7 Известно, что ряд сходится. Показать, что сходится и ряд Последний ряд получился из первого
- 20. 20. Если ряды сходятся и их суммы равны соответственно S’ и S’’,то и каждый из двух
- 21. Пример 8 Исследовать на сходимость ряд и если он сходится, найти его сумму S.
- 22. Решение Данный ряд м.б. представлен в виде или
- 23. Рассмотрим получившиеся два ряда и Т.к. они являются рядами убывающей геометрической прогрессии, то они сходятся и
- 24. Следовательно, данный ряд сходится и его сумма:
- 25. 30. Если в ряде добавить или отбросить конечное число членов, то полученный ряд сходится или расходится
- 26. Пример 9 Известно, что ряд сходится. Тогда сходящимся является и ряд: который получается из данного отбрасыванием
- 27. Сумма называется n-ым остатком ряда Т.к. остаток получается из данного ряда отбрасыванием, а данный ряд из
- 28. Если ряд сходится, то Т.е. остаток стремится к нулю при неограниченном возрастании n. В вопросах приближенного
- 29. Четкое определение сходимости ряда, основанное на понятии предела последовательности частичных сумм, появилось лишь в начале XIX
- 30. 1.2. Необходимый признак сходимости ряда Если ряд сходится, то его общий член un→0 при неограниченном возрастании
- 31. Пример 10 Известно, что ряд сходится. Проверим необходимое условие Необходимое условие выполнено.
- 32. Пример 11 Ряд расходится, т.к. Необходимое условие не выполнено ⇒ряд расходится
- 33. Пример 12 Известно, что ряд гармонический . Необходимое условие сходимости ряда выполняется: Между тем этот ряд
- 34. Доказательство: Прологарифмируем по основанию е:
- 36. Пусть n = 1,2,3,4,5,… Тогда получаем:
- 37. Складывая эти неравенства, получим: Sn- частичная сумма гармонического ряда Поскольку то Ряд расходится.
- 39. Скачать презентацию
































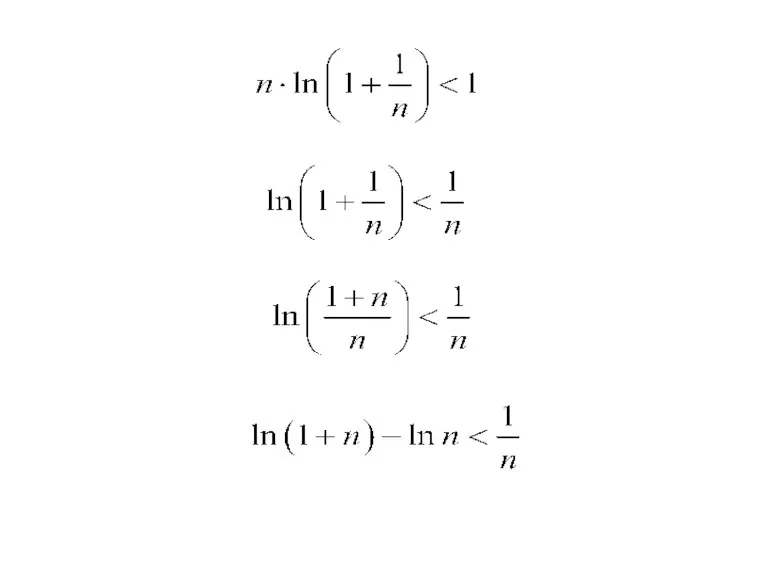
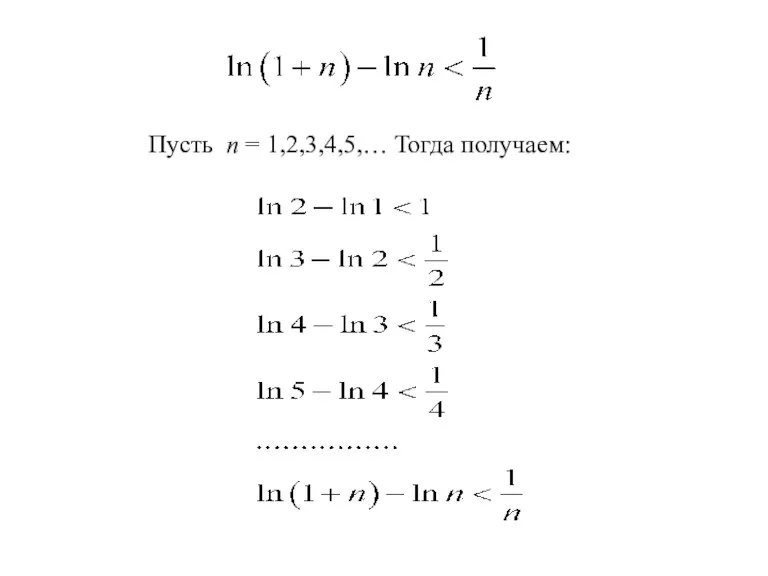

 Задачи на сложение и вычитание десятичных дробей
Задачи на сложение и вычитание десятичных дробей Десятичные дроби. Решение задач. Математика и экология (часть 2)
Десятичные дроби. Решение задач. Математика и экология (часть 2) Початкові та центральні моменти в теорії ймовірностей і математичній статистиці
Початкові та центральні моменти в теорії ймовірностей і математичній статистиці Гамильтоновы графы
Гамильтоновы графы Контрольная работа по математике 4 класс
Контрольная работа по математике 4 класс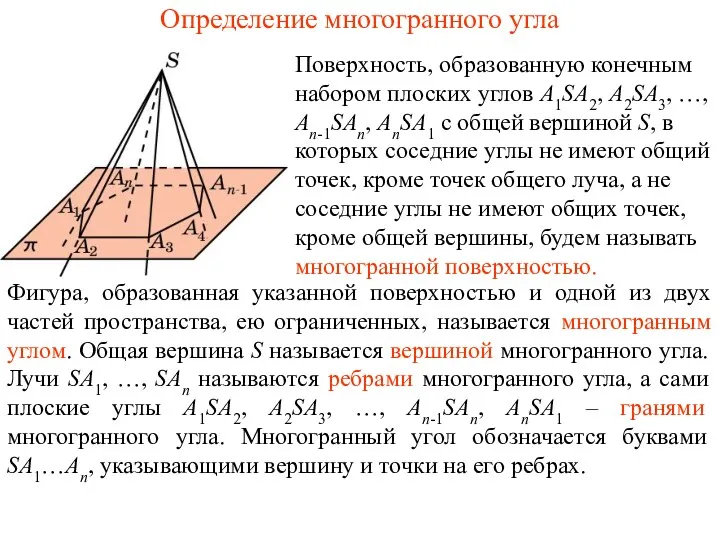 Определение многогранного угла
Определение многогранного угла Делители и кратные
Делители и кратные Деление и умножение обыкновенных дробей
Деление и умножение обыкновенных дробей Презентация занятия по математике часть 2 Диск
Презентация занятия по математике часть 2 Диск Прямоугольные треугольники и их свойства
Прямоугольные треугольники и их свойства Задачи на движение. ЕГЭ, математика
Задачи на движение. ЕГЭ, математика Мультимедийное пособие Функция
Мультимедийное пособие Функция Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Урок математики 1 класс Число один. Цифра 1
Урок математики 1 класс Число один. Цифра 1 Векторні величини. Метод координат
Векторні величини. Метод координат Числа, кратные 9
Числа, кратные 9 Авторское учебно-методическое пособие Счёт до 5
Авторское учебно-методическое пособие Счёт до 5 Аксонометрические построения. (Лекция 7)
Аксонометрические построения. (Лекция 7) Урок по математике - 4 на тему Вычитание смешанных дробей (Л.Г.Петерсон))
Урок по математике - 4 на тему Вычитание смешанных дробей (Л.Г.Петерсон)) Умножение и деление обыкновенных дробей. Систематизация и закрепление знаний, умений и навыков
Умножение и деление обыкновенных дробей. Систематизация и закрепление знаний, умений и навыков Аксиомы стереометрии. (10 класс)
Аксиомы стереометрии. (10 класс) Число 8. Цифра 8
Число 8. Цифра 8 Возможности формирования универсальных учебных действий (УУД) при изучении начального курса математики
Возможности формирования универсальных учебных действий (УУД) при изучении начального курса математики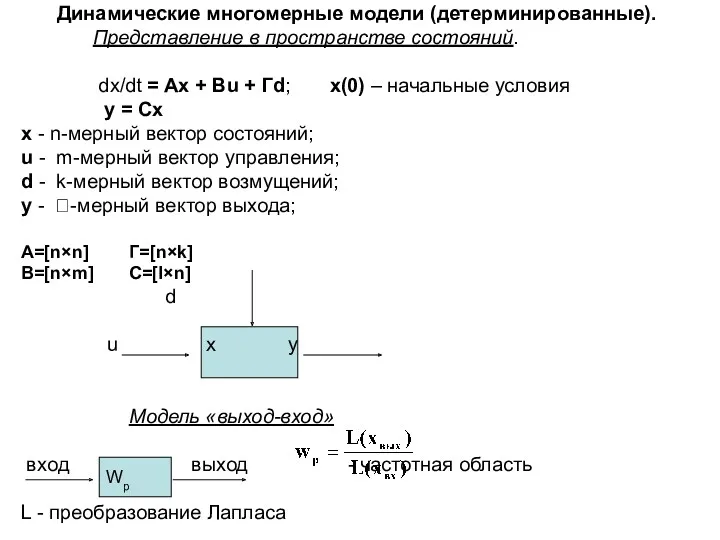 Динамические многомерные модели (детерминированные)
Динамические многомерные модели (детерминированные) презентация для уроков литературного чтения
презентация для уроков литературного чтения Действия с десятичными дробями в коррекционной школе. 8 класс
Действия с десятичными дробями в коррекционной школе. 8 класс Площади плоских фигур
Площади плоских фигур Сложная функция. Производная сложной функции
Сложная функция. Производная сложной функции