Содержание
- 2. Уильям Роуэн Гамильтон (William Rowan Hamilton, 1857). Вершина – город. Игра – найти путь через все
- 3. Цель игры – найти цикл графа, проходящего через каждую вершину. Определение. Любой цикл графа, обладающий таким
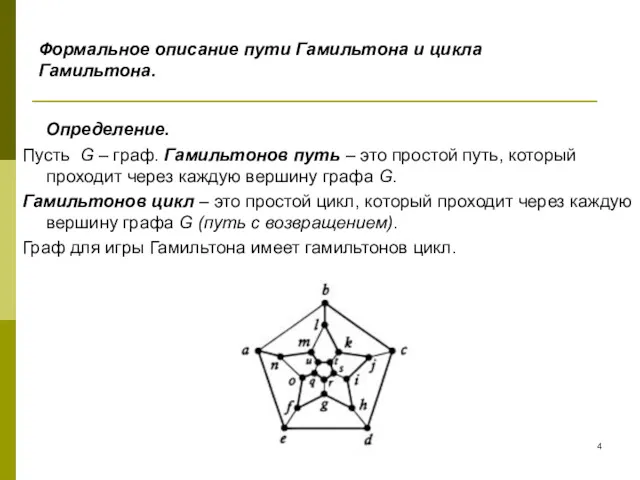
- 4. Формальное описание пути Гамильтона и цикла Гамильтона. Определение. Пусть G – граф. Гамильтонов путь – это
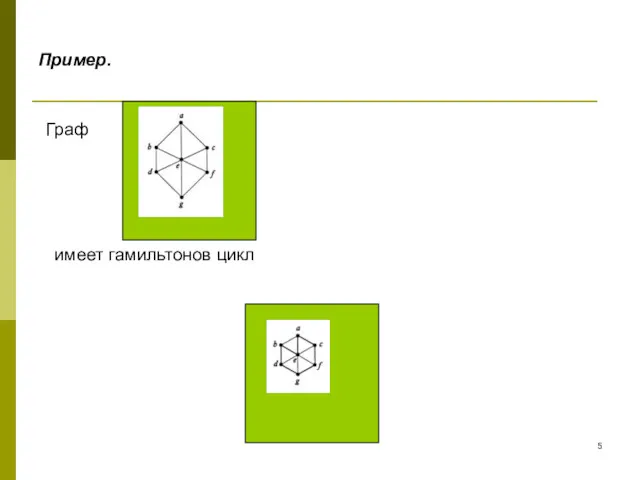
- 5. Пример. Граф имеет гамильтонов цикл
- 6. Пример. Гиперкуб порядка n > 3 имеет гамильтонов цикл. Его код Грея: Гамильтонов цикл для гиперкуба
- 7. Пример. Полный граф Kn при n ≥ 3 имеет гамильтонов цикл. Пусть v1, v2, v3, …
- 8. Теорема. Для любой вершины из цикла Гамильтона существует ровно два ребра из этого цикла, инцидентные данной
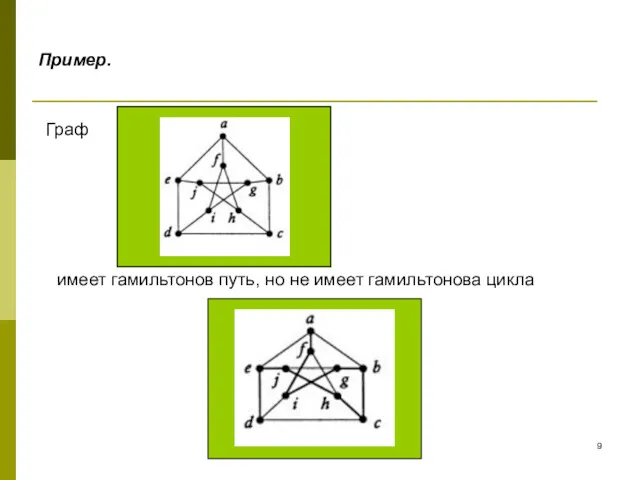
- 9. Пример. Граф имеет гамильтонов путь, но не имеет гамильтонова цикла
- 10. Чтобы граф имел гамильтонов цикл, степень каждой вершины должна быть не меньше 2-х. Граф должен быть
- 11. Теорема. Если G(V, E) - связный граф с n вершинами, где n ≥ 3, и для
- 12. Теорема. Пусть G(V, E) - связный граф с n ≥ 3 вершинами и пусть u и
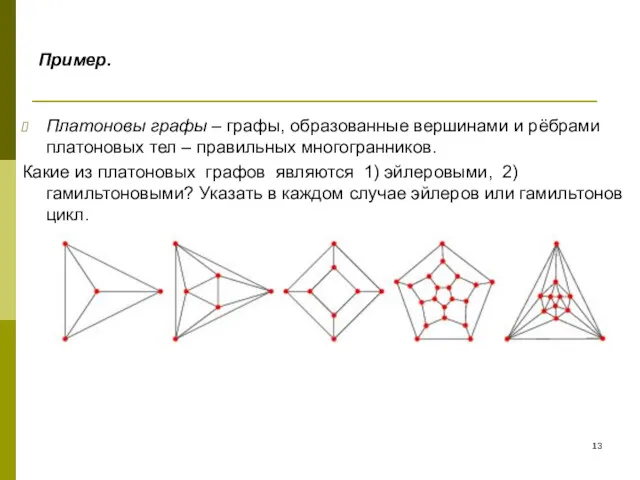
- 13. Пример. Платоновы графы – графы, образованные вершинами и рёбрами платоновых тел – правильных многогранников. Какие из
- 14. Определение. Пусть имеется граф G с n вершинами. Добавим ребра к несмежным вершинам u и v
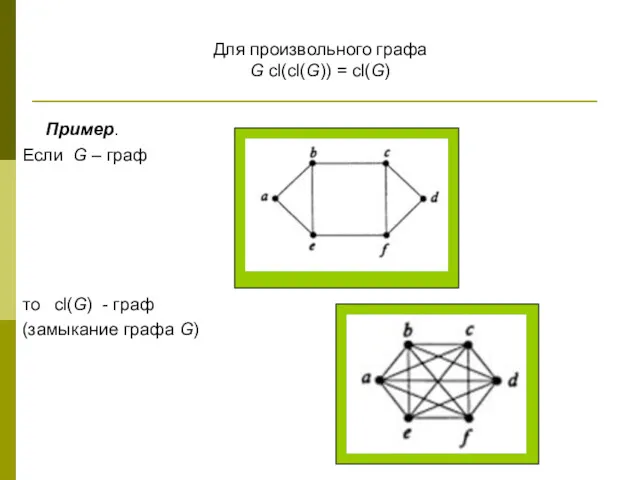
- 15. Для произвольного графа G cl(cl(G)) = cl(G) Пример. Если G – граф то cl(G) - граф
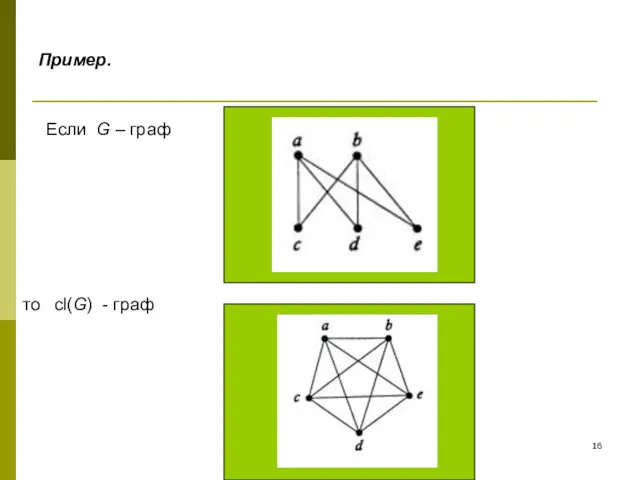
- 16. Пример. Если G – граф то cl(G) - граф
- 17. Пример. Если G - полный двудольный граф Km,m при m ≥ 1, то cl(G) – полный
- 18. Взвешенные графы и алгоритмы поиска кратчайшего пути
- 19. Определение. Пусть A = (a1, a2, a3, … , an) и B = (b1, b2, b3,
- 20. Теорема. Пусть a = v1 и b = vn . Если v1, v2 , … ,
- 21. Отыскивается кратчайшее расстояние между v1 и vn
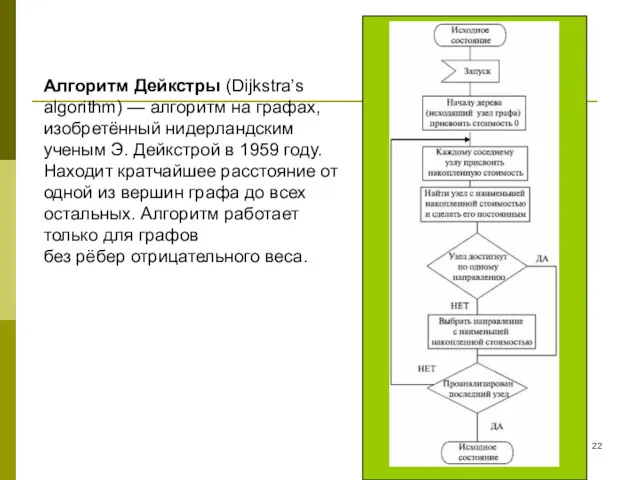
- 22. Алгоритм Дейкстры (Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году.
- 23. Примеры Пример 1. Дана сеть автомобильных дорог, соединяющих города Московской области. Некоторые дороги односторонние. Найти кратчайшие
- 24. Пример Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a.
- 25. Пример (продолжение) Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не
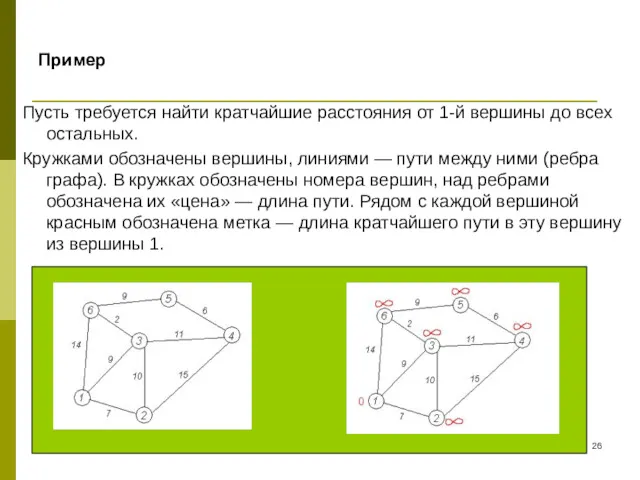
- 26. Пример Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных. Кружками обозначены вершины, линиями
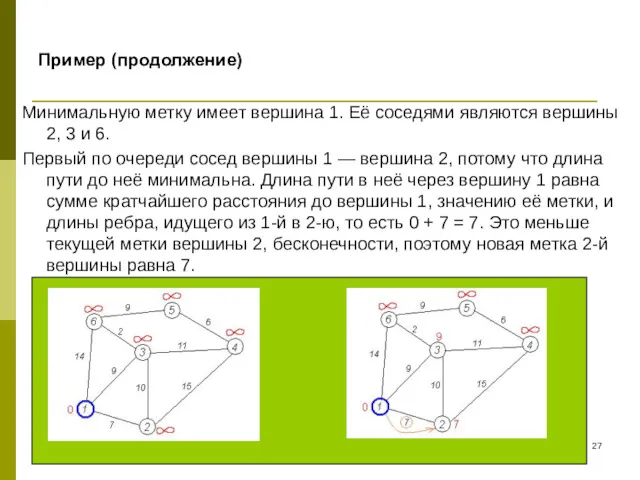
- 27. Пример (продолжение) Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Первый
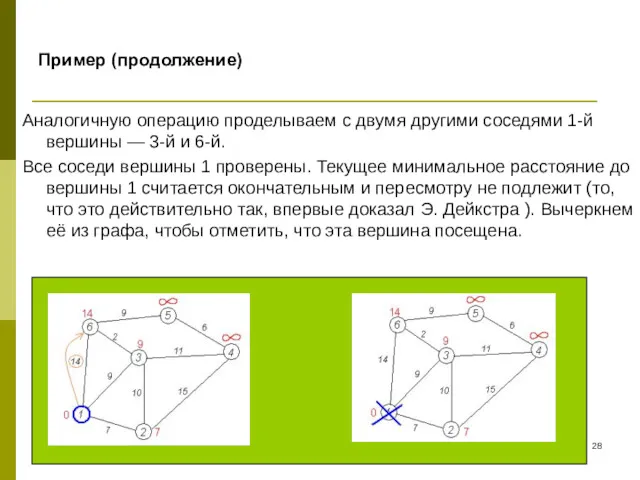
- 28. Пример (продолжение) Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й. Все
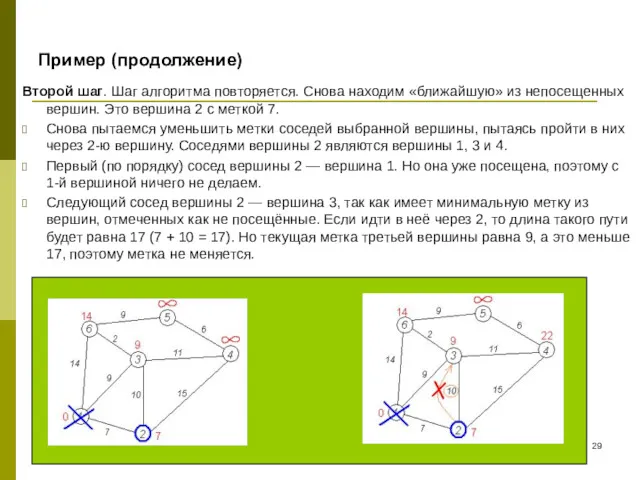
- 29. Пример (продолжение) Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2
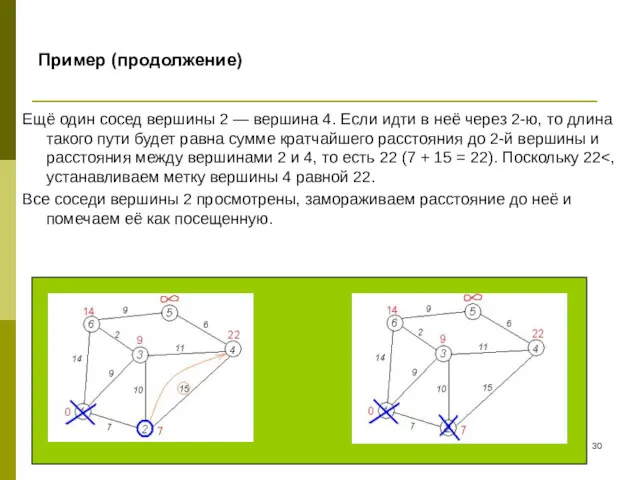
- 30. Пример (продолжение) Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю,
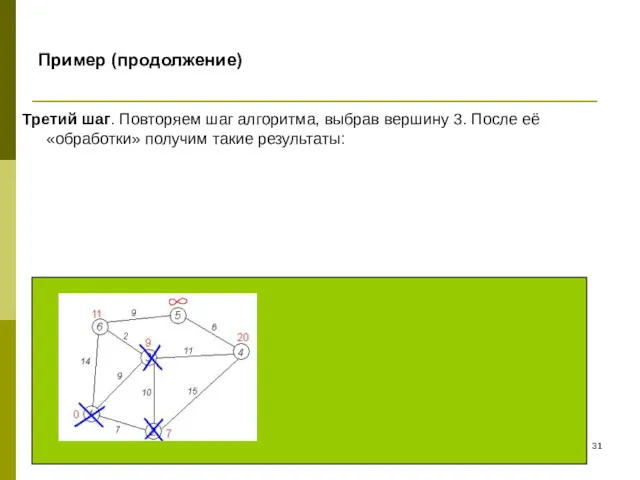
- 31. Пример (продолжение) Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
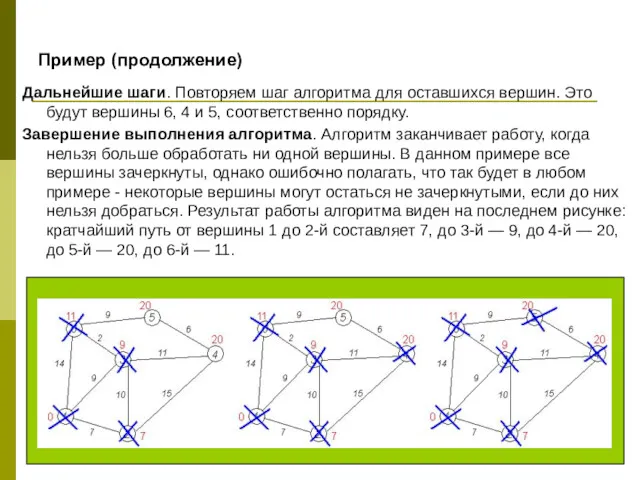
- 32. Пример (продолжение) Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и
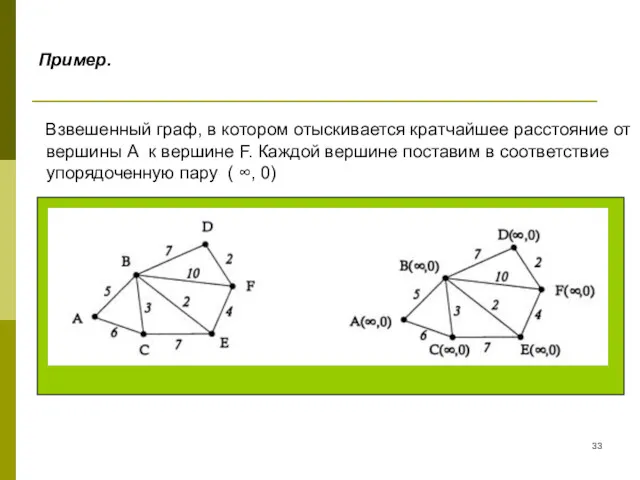
- 33. Пример. Взвешенный граф, в котором отыскивается кратчайшее расстояние от вершины А к вершине F. Каждой вершине
- 34. В алгоритме для кратчайшего расстояния между двумя вершинами использованы матрицы
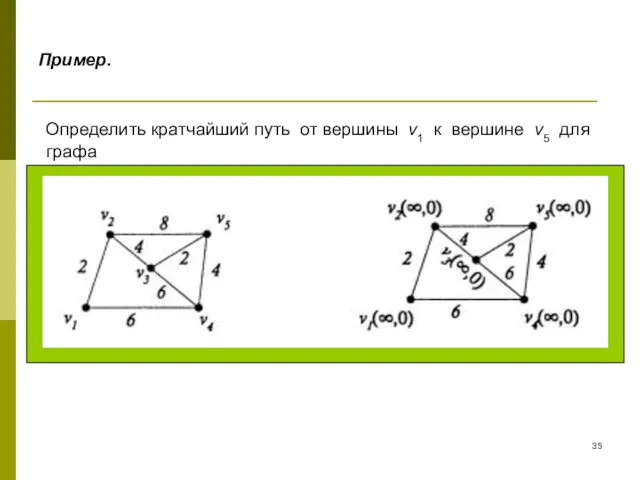
- 35. Пример. Определить кратчайший путь от вершины v1 к вершине v5 для графа
- 36. Алгоритм более удобен для вычисления вручную
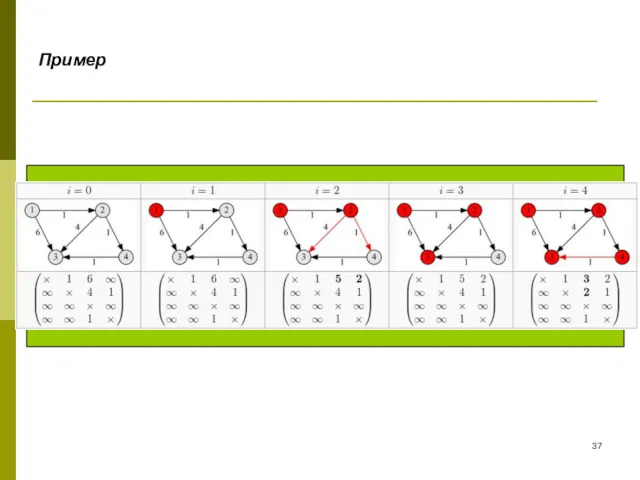
- 37. Пример
- 38. Алгоритм более удобен для вычисления на компьютере
- 40. Скачать презентацию




















 Площадь прямоугольника
Площадь прямоугольника Кривые второго порядка
Кривые второго порядка Отношение двух чисел. Работа с математической моделью
Отношение двух чисел. Работа с математической моделью Математика. 1 класс. Урок 37. Числа 1-6 - Презентация
Математика. 1 класс. Урок 37. Числа 1-6 - Презентация Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов
Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов Сложение и вычитание обыкновенных дробей с разными знаменателями
Сложение и вычитание обыкновенных дробей с разными знаменателями Методы поиска условного экстремума
Методы поиска условного экстремума Множества. Операции над множествами
Множества. Операции над множествами Урок 11. Деление многозначного числа на многозначное с однозначным частным
Урок 11. Деление многозначного числа на многозначное с однозначным частным Математика в кулінарії
Математика в кулінарії Урок - игра. Тема: Производная и интеграл
Урок - игра. Тема: Производная и интеграл Введение в эконометрику
Введение в эконометрику Упрощение выражений, задачи на части, порядок действий
Упрощение выражений, задачи на части, порядок действий Приближенное вычисление корня
Приближенное вычисление корня О великом Пифагоре
О великом Пифагоре Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Комплексные числа. История возникновения
Комплексные числа. История возникновения Линейная и квадратичная функции и их графики
Линейная и квадратичная функции и их графики Касательная к графику функции
Касательная к графику функции Решение примеров. Прибавление числа 10
Решение примеров. Прибавление числа 10 Координатный луч
Координатный луч Формирование элементарных математических представлений в подготовительной группе. Путешествие карандаша
Формирование элементарных математических представлений в подготовительной группе. Путешествие карандаша Начала математического анализа
Начала математического анализа Дидактические пособия по ФЭМП
Дидактические пособия по ФЭМП Использование корреляционно-регрессионного анализа в управлении предприятием
Использование корреляционно-регрессионного анализа в управлении предприятием Теория поверхностей. Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности
Теория поверхностей. Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности 20191128_prezentatsiya_ugly
20191128_prezentatsiya_ugly Деление на 2
Деление на 2