Содержание
- 2. 2.1. Силовые линии электростатического поля Теорема Остроградского-Гаусса устанавливает связь между электрическими зарядами и электрическим полем. Она
- 3. Остроградский Михаил Васильевич (1801 – 1862) отечественный математик и механик. Учился в Харьковском ун-те (1816 –
- 4. Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик. Исследования посвящены многим разделам физики.
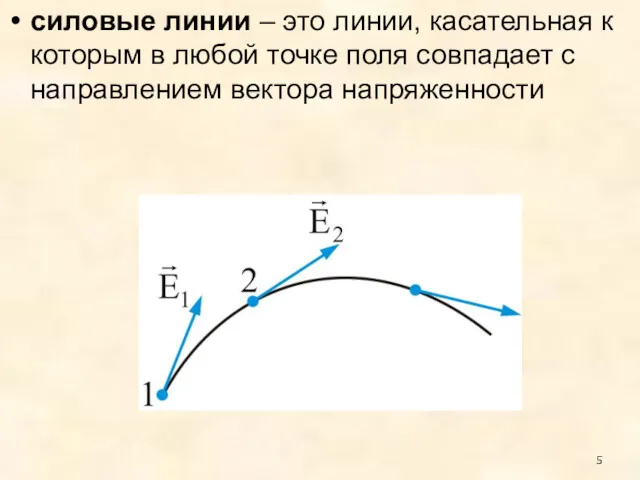
- 5. силовые линии – это линии, касательная к которым в любой точке поля совпадает с направлением вектора
- 6. Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению Однородное электростатическое
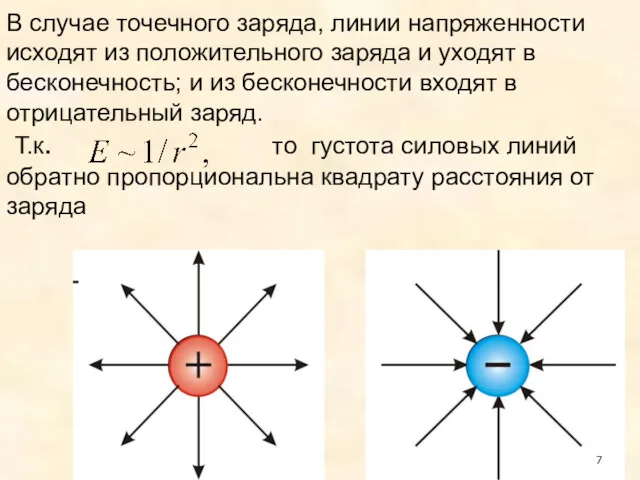
- 7. В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из
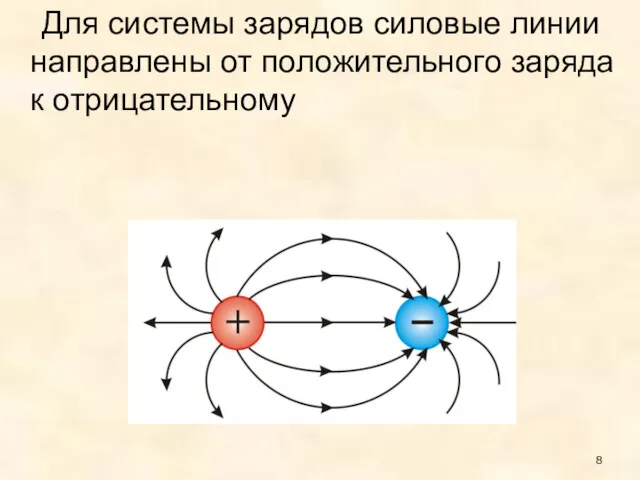
- 8. Для системы зарядов силовые линии направлены от положительного заряда к отрицательному
- 10. Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их
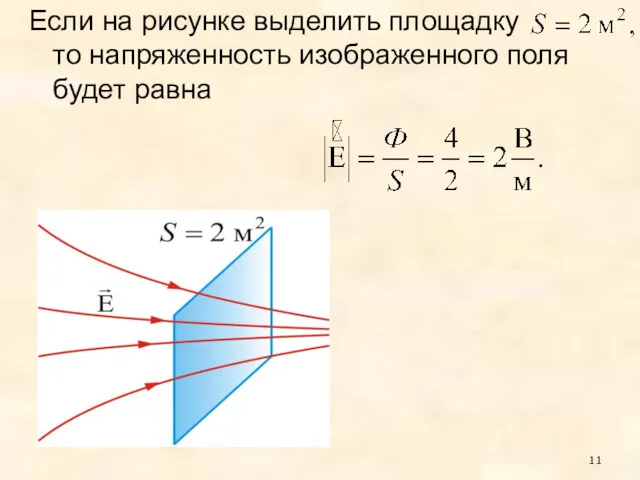
- 11. Если на рисунке выделить площадку то напряженность изображенного поля будет равна
- 12. 2.2. Поток вектора напряженности Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности
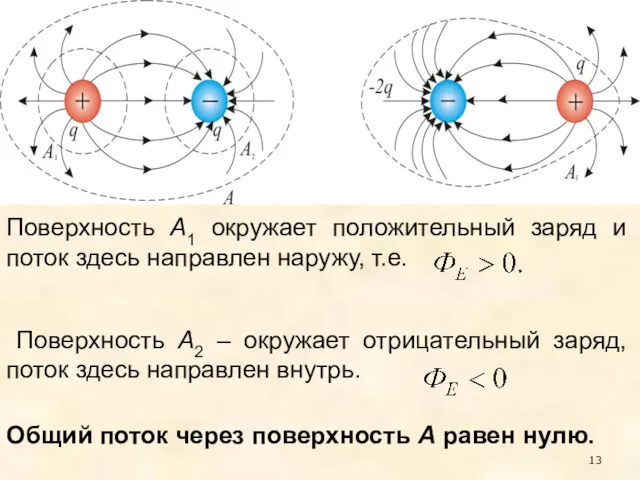
- 13. Поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е. Поверхность А2 – окружает отрицательный
- 14. Поток вектора напряженности через произвольную элементарную площадку dS будет равен: В однородном поле В произвольном электрическом
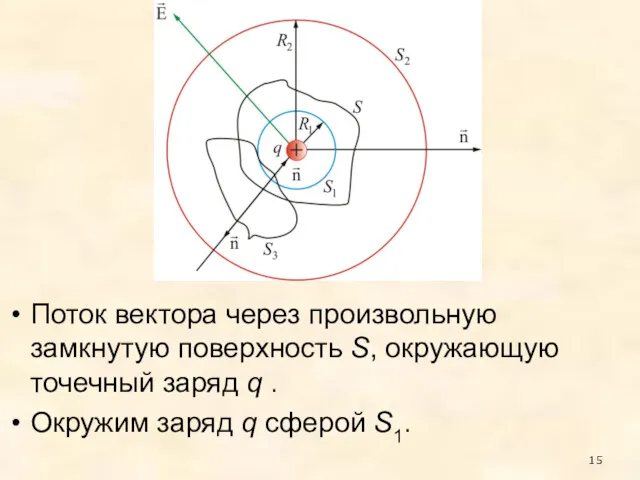
- 15. Поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд q . Окружим заряд q сферой
- 16. Центр сферы совпадает с центром заряда. Радиус сферы S1 равен R1. В каждой точке поверхности S1
- 17. Поток через сферу S2, имеющую радиус R2:
- 18. Из непрерывности линии следует, что поток и через любую произвольную поверхность S будет равен этой же
- 19. Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности: – теорема Гаусса для нескольких зарядов: Поток
- 20. Полный поток проходящий через S3, не охватывающую заряд q, равен нулю: Таким образом, для точечного заряда
- 21. Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах пространства: Суммарный заряд
- 22. 2.4. Дифференциальная форма теоремы Остроградского-Гаусса Пусть заряд распределен в пространстве ΔV, с объемной плотностью . Тогда
- 23. При или Величину, являющуюся пределом отношения к ΔV, при , называют дивергенцией поля Е
- 24. Дивергенция поля Е . Дивергенция - скалярная функция координат. В декартовой системе координат
- 25. Таким образом Это теорема Остроградского-Гаусса в дифференциальной форме. Введем векторный дифференциальный оператор (Набла) где i, j,
- 26. Сам по себе оператор смысла не имеет. Он приобретает смысл в сочетании с векторной или скалярной
- 27. В тех точках поля, где – источники поля (положительные заряды), В тех точках поля, где –
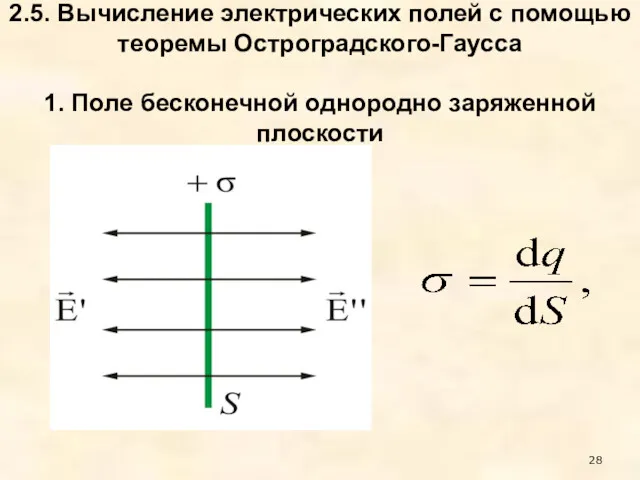
- 28. 2.5. Вычисление электрических полей с помощью теоремы Остроградского-Гаусса 1. Поле бесконечной однородно заряженной плоскости
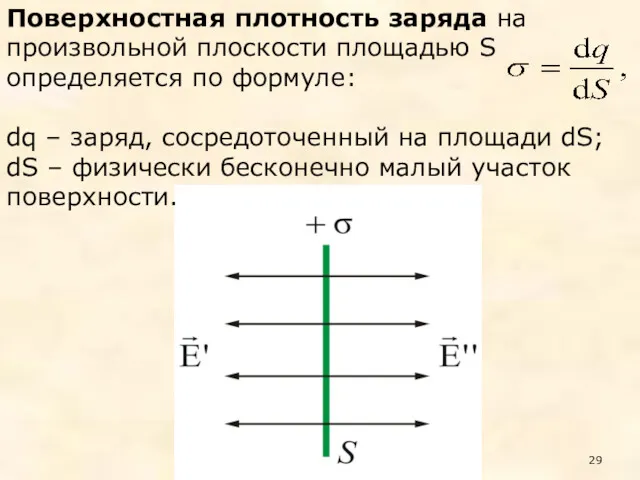
- 29. Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: dq – заряд, сосредоточенный на
- 30. Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости Тогда
- 31. Суммарный поток через замкнутую поверхность (цилиндр) будет равен: Внутри поверхности заключен заряд. Следовательно, из теоремы Остроградского-Гаусса
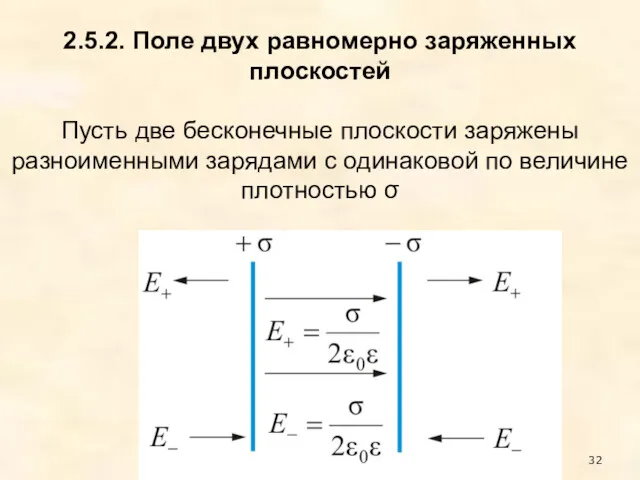
- 32. 2.5.2. Поле двух равномерно заряженных плоскостей Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по
- 33. Результирующее поле, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей Вне плоскостей напряженность
- 34. Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке:
- 35. Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин): Механические силы, действующие между заряженными
- 36. Сила притяжения между пластинами конденсатора: где S – площадь обкладок конденсатора. Т.к. Это формула для расчета
- 37. 2.5.3. Поле заряженного бесконечного цилиндра (нити) Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с
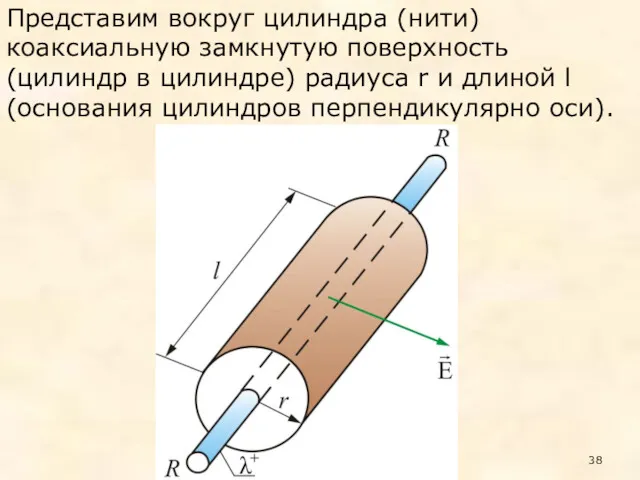
- 38. Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания
- 39. Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r. Следовательно, поток вектора через рассматриваемую
- 40. При на поверхности будет заряд По теореме Остроградского-Гаусса Тогда Если , т.к. внутри замкнутой поверхности зарядов
- 41. График распределения напряженности электростатического поля цилиндра
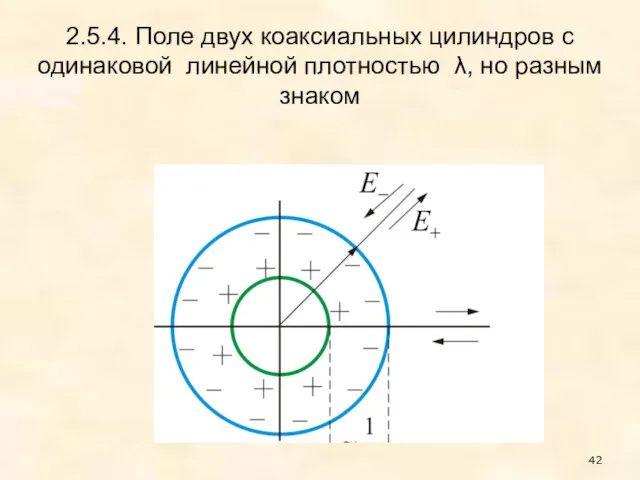
- 42. 2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
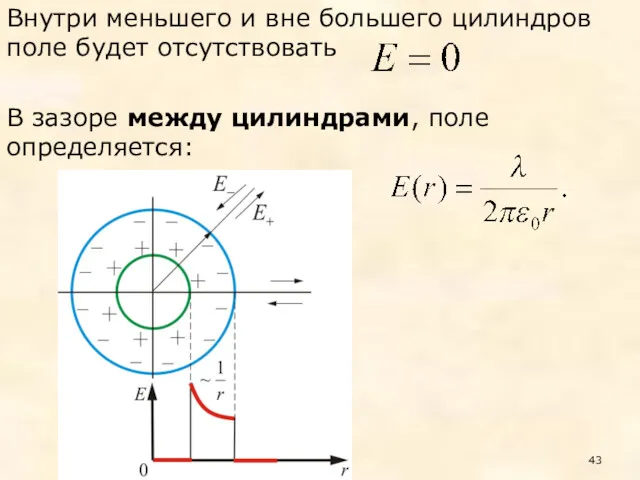
- 43. Внутри меньшего и вне большего цилиндров поле будет отсутствовать В зазоре между цилиндрами, поле определяется:
- 44. Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами
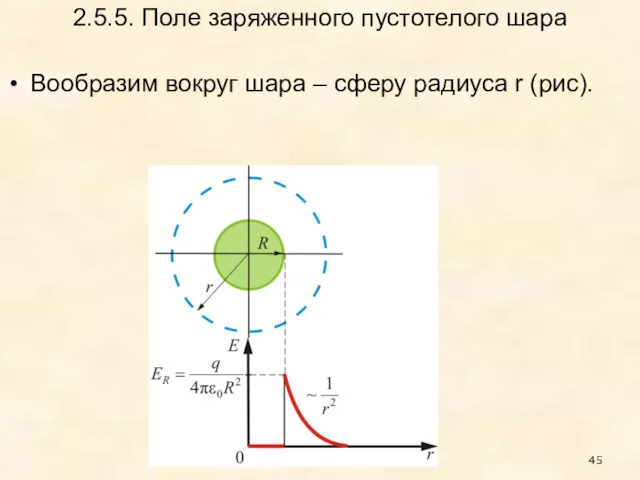
- 45. 2.5.5. Поле заряженного пустотелого шара Вообразим вокруг шара – сферу радиуса r (рис).
- 46. Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда откуда поле вне
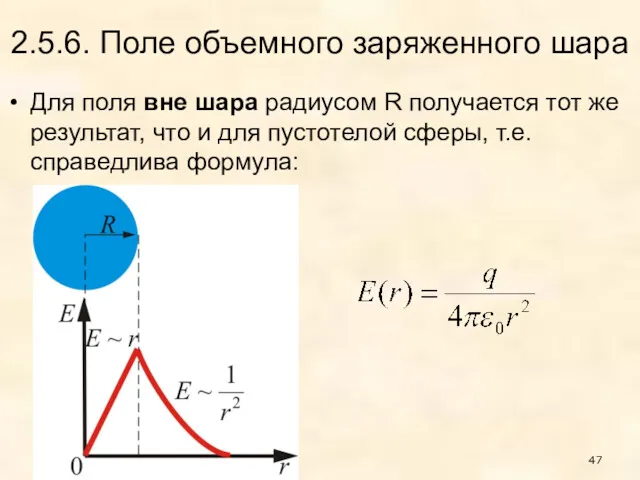
- 47. 2.5.6. Поле объемного заряженного шара Для поля вне шара радиусом R получается тот же результат, что
- 48. Внутри шара при сферическая поверхность будет содержать в себе заряд, равный где ρ – объемная плотность
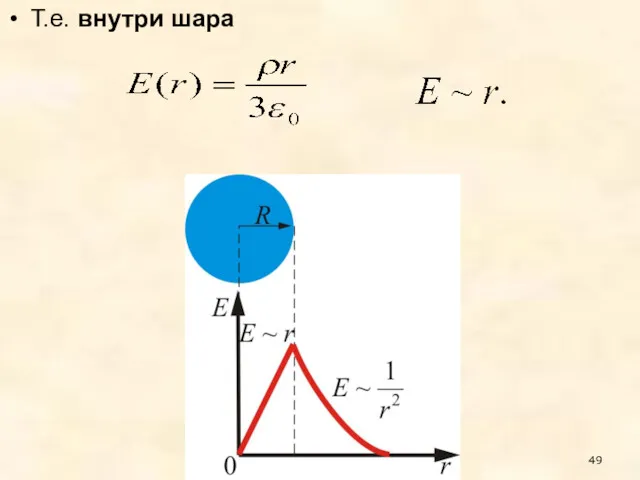
- 49. Т.е. внутри шара
- 51. Скачать презентацию

































 Теплотехника. Термодинамика открытых систем
Теплотехника. Термодинамика открытых систем Физика в професії кухаря
Физика в професії кухаря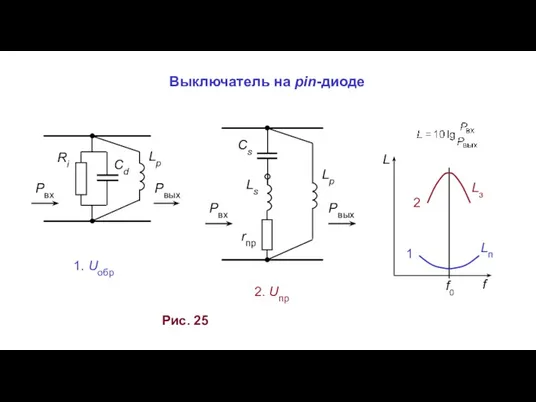 Выключатель на pin-диоде. Антенный переключатель. Стабилизатор мощности
Выключатель на pin-диоде. Антенный переключатель. Стабилизатор мощности Електрика в житті людини
Електрика в житті людини Ременные передачи
Ременные передачи Источники звука и звуковые колебания
Источники звука и звуковые колебания Зарождения ракетных двигателей
Зарождения ракетных двигателей Биологическое действие радиации. Закон радиоактивного распада. 9 класс
Биологическое действие радиации. Закон радиоактивного распада. 9 класс Тормозные системы
Тормозные системы Повторение по теме Законы движения и взаимодействия тел
Повторение по теме Законы движения и взаимодействия тел Ішкi энергия. Ішкi энергияны өзгерту тәсiлдерi
Ішкi энергия. Ішкi энергияны өзгерту тәсiлдерi электрический ток в металлах
электрический ток в металлах Ультрақысқа толқындар
Ультрақысқа толқындар Принцип Гюйгенса. Закон отражения света
Принцип Гюйгенса. Закон отражения света Ремонт автомобилей. Классификация способов восстановления деталей. (Тема 3.1)
Ремонт автомобилей. Классификация способов восстановления деталей. (Тема 3.1) Работа и мощность электрического тока
Работа и мощность электрического тока Электромагнитная волна, поляризация ЭМВ
Электромагнитная волна, поляризация ЭМВ Механизмы поворота. Устройство и расчет. (Лекция № 5)
Механизмы поворота. Устройство и расчет. (Лекция № 5) Альфа-распад
Альфа-распад Барометрическая формула. (Лекция 6)
Барометрическая формула. (Лекция 6) Lektsia_9_Difraktsia_Frenelya
Lektsia_9_Difraktsia_Frenelya Kiyi ve liman yapilari
Kiyi ve liman yapilari Презентация к уроку физики по теме: Электрическое сопротивление
Презентация к уроку физики по теме: Электрическое сопротивление Движение под действием силы тяжести. Решение задач
Движение под действием силы тяжести. Решение задач Master thesis
Master thesis Законы Ньютона
Законы Ньютона Потенциальная и кинетическая энергия
Потенциальная и кинетическая энергия Эхометод измерения глубины
Эхометод измерения глубины